2.3.4 Определение расстояния между деталями
Расстояние между внешними поверхностями передачи, L, мм, рассчитывается по формуле
L
=
+ aw
(55)
L = + 0 = 0 мм.
Зазор между колесами и стенками корпуса, А, мм, определяется по формуле
А
=
+3 (56)
А
=
+ 3 = 0,0 мм.
Принимаем А = 0 мм.
Расстояние между дном корпуса и поверхностью колеса, А1, мм, определяется следующим образом
А1 ≥ 4А (57)
А1 ≥ 4 · 11 ≥ 44 мм.
Принимаем А1 = 44 мм.
Проверяем условие типа смазки подшипников
n22 · dа2 = 0,02 · 0,0 = 0 > 100.
Принимаем картерную смазку подшипников с закладными крышками.
Диаметр фундаментных болтов, d1, мм рассчитывается по формуле
d1 = (0,030…0,036) · аw + 12 (58)
d1 = (0,030…0,036) · 0 + 12 = 0,0…0 мм.
Принимаем d1 = 0 мм.
Диаметр болтов у подшипников, d2, мм, можем определить по формуле
d2 = (0,70…0,75) · d1 (59)
d2 = (0,70…0,75) · 0 = 0…0 мм.
Принимаем d2 = 14 мм.
Толщина стенки корпуса редуктора, δ, мм определяется следующим образом
δ = 0,025 · аw + 1 (60)
δ = 0,025 · 0 + 1 = 0,0 мм < 0 мм.
Принимаем δ = 8 мм.
Параметр бобышки К2 = 36 мм.
Длина бобышки, IБ, мм, рассчитывается по формуле
IБ = δ + К2 + (3…5) (61)
IБ = 0 + 0 + (3…5) = 0…0 мм.
Принимаем IБ = 48 мм.
Расстояние между опорами быстроходного вала, I1, мм, определяем по формуле
I1 = b1 + 2А + В1 + (2…4), (62)
где В1 –ширина колец подшипников быстроходного вала, В1 = 0 мм;
b1 – ширина венца шестерни, b1 = 0 мм.
I1 = 0 + 2 · 0 + 0 + (2…4) = 0…0 мм.
Принимаем I1 = 0 мм.
Расстояние от бобышки до участков валов с диаметрами d1 и d2, I1' и I2', мм, принимаем следующим образом
I1' = I2' = (0,6…0,8) · А (63)
I1' = I2' = (0,6…0,8) · 0 = 0,0…0,0 мм
Принимаем I1' = I2' = 0 мм.
Длина посадочного места под шкив ременной передачи, Iст1, мм, рассчитывается по формуле
Iст1 = (1,2…1,5) · d1 (64)
Iст1 = (1,2…1,5) · 0 = 0,0…0 мм.
Принимаем Iст1 = 0 мм.
Расстояние до точки приложения консольной нагрузки от шкива ременной передачи IК1, мм
IК1
= IБ
-
- (1 … 2) (65)
IК1
= 0 –
+ 0 +
- (1…2) = 0,0…0,0 мм.
Принимаем IК1 = 0 мм.
Расстояние между опорами тихоходного вала, I2, мм, определяем
I2 = b1 + 2А + В2 + (2…4), (66)
где В2 –ширина колец подшипников быстроходного вала, В2 = 0 мм;
b2 – ширина венца шестерни, b1 = 0 мм.
I2 = 0 + 2 · 0 + 0 + (2…4) = 0…0 мм.
Принимаем I2 = 0 мм.
Длина посадочного места под полумуфту, Iст2, мм, определяется по формуле
Iст2 = (1,0…1,5) · d2 (67)
Iст2 = (1,0…1,5) · 0 = 0…0 мм.
Принимаем Iст2 = 0 мм.
Расстояние до точки приложения консольной нагрузки от муфты, IК2, мм, рассчитывается по формуле
IК2
= IБ
-
+ I2'
+ IСТ2
– (1…2) (68)
IК2
= 48 -
+ 8 + 100 – (1…2) = 142…141 мм.
Принимаем IК2 =142 мм.
2.3.5 Первая эскизная компоновка редуктора
Первая эскизная компоновка редуктора выполняется в соответствии с размерами, полученными при проектном расчёте валов и определении расстояний между деталями (рисунок 10).
Зазор между наружными кольцами подшипников
Δ
= 2 ·
(69)
Δ
= 2 ·
= 0,0 мм.
Определяем требуемое межосевое расстояние по условию размещения подшипников
=
+ Δ ≤ аw
(70)
2.3.6. Определение реакций в опорах подшипников, построение эпюр крутящих и изгибающих моментов.
Вычерчиваем расчетную схему быстроходного вала (рисунок 11).
Строим эпюру крутящего момента МК1 = М2 = 0,0 Н·м.
Определяем реакции опор в вертикальной плоскости ХУ на основании равенств ΣМА(FК) = 0 и ΣМВ(FК) = 0, то есть
Ft1
∙
- RBY
∙ I1
= 0
следовательно
RBY
=
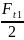
RAY =
RBY = = 0 Н
RAY = = 0 Н
Проверка: так как ΣFKY = 0, значит
RAY – Ft1 + RBY = 0
0 – 0 + 0 = 0.
Рисунок 10 – Првая эскизная компоновка
Определяем реакции опор в горизонтальной плоскости ХZ на основании выполнения равенств: ΣМА(FК) = 0 и ΣМВ(FК) = 0, то есть
-
Fврп
· IК1
+ Fr1
·
– RBZ
· I1
= 0
- Fврп · ( I1 + IK1) + RAZ · I1 – Fr1 · = 0
RBZ
=
RAZ
=
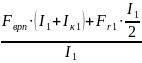
RBZ
=
= 0 Н
RAZ
=
= 0 Н.
Проверка: ΣFKz = 0
Fврп - RAZ + Fr1 - RBZ = 0
0 – 0 + 0 – 0 = 0
Суммарные радиальные реакции опор подшипников быстроходного вала, RA и RB, Н, рассчитываются по формулам
RA
=
RB
=
RA
=
= 0 Н
RB = = 0 Н.
Рисунок 11 – Эпюры быстроходного вала
Значения изгибающих моментов вертикальной плоскости, МEZ, H·м, определяются следующим образом
МЕZ = RAY ·
МЕZ = 0 · = 0 Н∙мм = 0,0 Н·м.
Определяем значения изгибающих моментов МY в горизонтальной плоскости
МАY = - Fврп · IК1
МЕУ = RBZ ·
МАY = - 0 · 0 = - 0 Н∙мм = - 0,0 Н·м
=
0 ·
= 0 Н∙мм = 0,0 Н·м.
Строим эпюры изгибающих моментов МZ и МY.
Суммарные изгибающие моменты в наиболее нагруженных сечениях быстроходного вала, МИА и МИУ, Н·м, определяются следующим образом
МИА = МАY
МИЕ
=
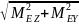
МИА = 0,0 Н·м
МИЕ
=
= 0,0 Н·м.
Вычерчиваем расчётную схему тихоходного вала (Рисунок 12).
Строим эпюру крутящего момента МК2 = М3 = 0,0 Н·м.
Определяем реакции опор в вертикальной плоскости ХУ на основании равенств: ΣМС(FК) = 0 и ΣМD(FК) = 0, то есть
-Ft2
·
+ RDY
· I2
+ FM
=
0
- RCY · I2 + Ft2 · + FM · IК2 = 0
RDY
=
RCY
=
RDY
=
= 0 Н
RCY
=
= 0 Н.
Проверка: ΣFКY = 0
- RCY + Ft2 – RDY – Fм = 0
- 0 + 0 – 0 - 0 = 0
Определяем реакции опор в горизонтальной плоскости ХZ на основании выполнения равенств: ΣМС(FК) = 0 и ΣМD(FК) = 0, то есть
- Fr2 · + RDZ · I2 = 0
- RCZ · I2 + Fr2 · = 0
RDZ
=
=
RCZ = =
RDZ = = 0 Н
RCZ = = 0 Н.
Проверка : ΣFKZ = 0; значит
RCZ – Fr2 + RDZ = 0
0 – 0 + 0 = 0
Суммарные радиальные реакции опор подшипников тихоходного вала, RC и RD, Н, рассчитываются по формулам
RC
=
RD
=
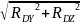
RC = = 0 Н
RD = = 0 Н.
Значение изгибающих моментов МZ в вертикальной плоскости, МEZ и МDZ, Н·м, определяются следующим образом
МFZ = - RCY ·
МDZ = - FМ · IК2
МFZ = - 0 · = - 0 Н∙мм = 0,0 Н·м
МDZ = - 0 · 0 = - 0 Н∙мм = - 0,0 Н·м.
Значения изгибающих моментов МY в горизонтальной плоскости МFY, Н·м, можно рассчитать по формулам
МFY = - RCZ ∙
МFY = - 0 ∙ = - 0 Н∙мм = - 0,0 Н∙м
Строим эпюры изгибающих моментов МZ и МY.
Суммарные изгибающие моменты в наиболее нагруженных сечениях тихоходного вала, МF, МD, Н·м, определяются по формулам
МF
=
МD = МDZ
МF
=
= 0,0 Н·м,
МD = 0,0 Н·м.