
Поразрядная сортировка
Во многих приложениях сортировки ключи, используемые для упорядочения записей в файлах, могут быть весьма сложными. Например, насколько сложны ключи, используемые в телефонной книге или в библиотечном каталоге. Сейчас мы рассмотрим другую абстракцию для ключей сортировки. Например, часто нет необходимости в полной обработке ключей на каждом этапе: при поиске в телефонном справочнике, чтобы найти страницу с номером какого-либо абонента, достаточно проверить лишь несколько первых букв его фамилии. Чтобы добиться такой же эффективности алгоритмов сортировки, мы перейдем от абстрактной операции сравнения ключей к абстракции, в которой ключи разбиваются на последовательность частей фиксированного размера — байтов. Методы сортировки, основанные на обработке ключей по частям, называются поразрядными методами сортировки (radix sort). Эти методы не просто сравнивают ключи, а обрабатывают и сравнивают части ключей.
Алгоритмы поразрядной сортировки интерпретируют ключи как числа, представленные в системе счисления с основанием R, при различных значениях R (основание системы счисления — radix), и работают с отдельными цифрами этих чисел. Алгоритмы поразрядной сортировки основаны на абстрактной операции " извлечь i-ю цифру ключа " .
Существуют два принципиально различных базовых подхода к поразрядной сортировке. Первый класс методов составляют алгоритмы, анализирующие цифры в ключах в направлении слева направо, при этом первыми обрабатываются наиболее значащие цифры. Все эти методы вместе называются MSD-сортировками (most significant digit radix sort — поразрядная сортировка сначала по старшей цифре). MSD-сортировки привлекательны тем, что они анализируют минимальный объем информации, необходимый для выполнения сортировки.
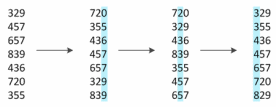
Во втором классе методов поразрядной сортировки используется другой принцип: они анализируют цифры ключей в направлении справа налево, работая сначала с наименее значащими цифрами. Все эти методы вместе называются LSD-сортировками (least significant digit radix sort — поразрядная сортировка сначала по младшей цифре). LSD-сортировка в какой-то степени противоречит интуиции, поскольку часть процессорного времени затрачивается на обработку цифр, которые не могут повлиять на результат, однако данная проблема легко решается, и этот почтенный метод годится для работы во многих приложениях сортировки.

#include <algorithm>
#include <iostream>
#include <iterator>
// Radix sort comparator for 32-bit two's complement integers
class radix_test
{
const int bit; // bit position [0..31] to examine
public:
radix_test(int offset) : bit(offset) {} // constructor
bool operator()(int value) const // function call operator
{
if (bit == 31) // sign bit
return value < 0; // negative int to left partition
else
return !(value & (1 << bit)); // 0 bit to left partition
}
};
// Least significant digit radix sort
void lsd_radix_sort(int *first, int *last)
{
for (int lsb = 0; lsb < 32; ++lsb) // least-significant-bit
{
std::stable_partition(first, last, radix_test(lsb));
}
}
// Most significant digit radix sort (recursive)
void msd_radix_sort(int *first, int *last, int msb = 31)
{
if (first != last && msb >= 0)
{
int *mid = std::partition(first, last, radix_test(msb));
msb--; // decrement most-significant-bit
msd_radix_sort(first, mid, msb); // sort left partition
msd_radix_sort(mid, last, msb); // sort right partition
}
}
// test radix_sort
int main()
{
int data[] = { 170, 45, 75, -90, -802, 24, 2, 66 };
lsd_radix_sort(data, data + 8);
// msd_radix_sort(data, data + 8);
std::copy(data, data + 8, std::ostream_iterator<int>(std::cout, " "));
return 0;
}
