Содержание

Введение 2

Глава 1. Понятие о комплексных частотных характеристиках. 4

Глава 2. Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов. 11

Глава 3. Комплексные частотные характеристики цепей с одним реактивным элементом. 15

Заключение. 22

Список литературы 24

Введение

Теория цепей является важнейшим инструментом, широко используемым в двух смежных направлениях науки и техники электротехнике и радиоэлектронике. Эти два направления имеют между собой много общего, построены на общей физической основе, но решают различные технические задачи В радиоэлектронике решается широкий круг задач, связанных с использованием электрических явлений для передачи и обработки информации. Сюда в первую очередь относятся задачи связи, радиолокации и радионавигации, телеуправление, телеизмерение, автоматизация различных производственных процессов и многие другие.

Во всех электротехнических и радиоэлектронных устройствах независимо от их назначения и принципа действия имеют место одни и тем же электромагнитные процессы, подчиняющиеся одним и тем же физическим законам. Электромагнитные явления и устройства на их основе можно достаточно строго описать методами теории электромагнитного поля. В теории электромагнитного поля оперируют с векторными величинами, такими, как плотность токов, напряженности электрического и магнитного полей. Эта теория позволяет описать процессы в каждой точке электромагнитного поля с помощью дифференциальных уравнений в частных производных (уравнение Максвелла)

Для исследования широкого круга устройств можно применить упрошенные методы, так называемые методы теории цепей, основанные на замене реального устройства некоторой упрощенной моделью, процессы в которой описываются скалярными величинами токами и напряжениями. Остальные составные части устройства при этом заменяют моделями, приближенно отражающими основные свойства соответствующих элементов.

Разработка инженерных методов исследования процессов в электротехнических и радиоэлектронных устройствах, основанных на замене этих устройств упрощенными моделями, составляет предмет теория цепей.

Однако методы теории электрических цепей вследствие принятых допущений и упрощений менее универсальны, чем методы теория поля, в частности их нельзя применять на достаточно высоких частотах, когда длина волны электромагнитных колебаний становится соизмеримой с размерами исследуемого устройства, а также при исследовании процессов излучения, распространения и приема радиоволн ограничено применение методов теории электрических цепей в технике высоких напряжений, при определение параметров и построение упрощенных моделей различных элементов цепей. В этих случаях для исследования процессов, а также для оценки пределов применимости результатов, полученных с помощью теории цепей, необходимо использовать методы теории электромагнитного поля.

Глава 1. Понятие о комплексных частотных характеристиках.

Задача анализа электрической цепи была сформулирована ранее как задача определения реакции цепи на заданное внешнее воздейст­вие. Пусть для некоторой линейной электрической цепи это воздействие задано в виде токов и напряжений нескольких независимых источни­ков тока и напряжения, а искомая реакция (отклик) цепи представля­ет собой совокупность токов или напряжений отдельных элементов (нагрузок).

Вынесем из рассматриваемой цепи все ветви, содержащие независимые источники тока и напряжения, а также ветви, токи или напряжения которых подлежат определению. Оставшуюся часть цепи, содержащую идеализированные пассивные элементы и, возможно, уп­равляемые источники, представим в виде многополюсника (рис.1,а).

Уточним понятия входов и выходов цепи. Входными будем называть пару зажимов (полюсов), к которым подключается каждый из независимых источников, задающих внешнее воздействие на цепь. Зажимы, служащие для подключения нагрузки, т. е. ветви, ток или на­пряжение которой необходимо определить, назовем выходными.

Пары входных и выходных зажимов образуют соответственно входы и выходы цепи, точнее, входы и выходы многополюсника, который получается из цепи при вынесении из нее источников внешнего воздей­ствия и нагрузок.

Деление зажимов на входные и выходные является в некоторой степени условным, так |как одна и та же пара зажимов может одновременно быть и входной, и выходной (например, когда внешнее воздействие на цепь задается некоторым независимым источником на­пряжения и требуется определить ток ветви, содержащей этот источ­ник). В связи с этим наряду с понятиями входа и выхода в теории це­пей широко используется понятие стороны многополюсника.

Стороной многополюсника, или портом, назы­вается пара зажимов, которые служат либо входом, либо выходом, ли­бо и входом и выходом одновременно. Из определений входных и выходных зажимов следуют важные осо­бенности зажимов, образующих порт многополюсника:

1. ток, втекающий через один зажим порта, равен току, вытекаю­щему через другой зажим этого же порта;

2. между парами полюсов, принадлежащих к разным портам, «е должно быть никаких внешних по отношению к многополюснику соеди­нений (внутри мгонополюсника соединения, естественно могут быть).

Зажимы, образующие одну сторону многополюсника, будем обо­значать одинаковыми цифрами (со штрихом и без штриха) 1 — Г, 2— —2', ..., п — п' (рис.1).

Рнс.1. Представление цепи в виде многополюсника

В зависимости от числа сторон различают односторонние, двусторон­ние и л-сторонние много­полюсники.

Пусть внешнее воздей­ствие на цепь задано только на одной паре полюсов v — v': х (i) = x_v (t) и не­обходимо найти реакцию цепи также только на од­ной паре полюсов r—r' (рис.1, б): (t).

Поскольку процессы на остальных полюсах в дан­ном случае интереса не представляют, их можно не выделять из цепи.

Ис­следуемую цепь удобно рассматривать как двусторонний четырехпо­люсник. Если 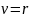то исследуемая цепь становится односторонней, т. е. превращается в двухполюсник (рис1, в).

Ограничимся рассмотрением случая гармонического внешнего воз­действия; при этом от исследования соотношений между мгновенными значениями реакции цепи y_r (t) и внешнего воздействия x_v (t)можно перейти к исследованию соотношений между их комплексными изобра­жениями.

По определению комплексной частотной характеристикой цепи называют отношение комплексных изображений отклика и воздействия:

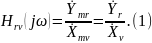
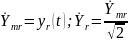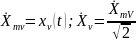Здесь –комплексные амплитуды и действующие значение реакции цепи; - комплексные амплитуды и действующие значение внешнего воздействия; r- номер выходных зажимов; v – номер входных зажимов.

Размерность комплексной частотной характеристики (КЧХ) равна отношению размерностей отклика цепи и внешнего воздействия. В за­висимости от того, какие величины (токи или напряжения) рассмат­риваются в качестве откликов и внешних воздействий, КЧХ может иметь размерность сопротивления (внешнее воздействие — i_v реакция цепи — u_r), проводимости (внешнее воздействие—u_v> реакция цепи — i_k) или быть безразмерной (внешнее воздействие — u_v и реакция це­пи — и* либо внешнее воздействие — t_v и реакция цепи — i_h).

Как и всякое комплексное число, КЧХ цепи может быть записана в показательной

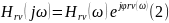
Или в алгебраической

формах. Представляя комплексные изображения отклика воздействия в показательной форме.

( (4)

и подставляя (4) в выражение (1), определяем модуль и аргумент КЧХ:

(5)

Таким образом, модуль КЧХ равен отношению амплитуд или действующих значений отклика цепи н внешнего воздействия, а ее аргумент представляет собой разность начальных фаз отклика и внешнего воздействия.

Если , КЧХ определяется выражением

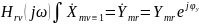(6)

следовательно, КЧХ цепи числено равна комплексной амплитуде ре­акции цепи на внешнее воздействие с единичной амплитудой и нулевой начальной фазой.

Зависимости модуля 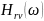и аргумента 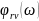комплексной час­тотной характеристики от частоты со называются амплитудно- частотной (АЧХ) и фазо-частотной (ФЧХ) характерис­тиками цепи.

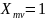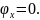Из сравнения выражений (2) и (6) видно, что АЧХ и ФЧХ цепи характеризуют зависимости от частоты соответственно ам­плитуды и начальной фазы отклика цепи на внешнее воздействие с и Таким образом, КЧХ сочетает в себе амплитудно- частотную и фазо-частотную характеристики цепи.

При графическом представлении комплексных частотных характе­ристик цепи обычно строят либо отдельно АЧХ и ФЧХ, либо изобра­жают зависимости от частоты вещественной (со) и мнимой 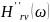составляющих КЧХ, которые однозначно выражаются через :

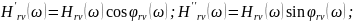
Комплексную частотную характеристику можно изобразить и в виде одной зависимости—годографа КЧХ, построенного на комплекс­ной плоскости. Годограф КЧХ представляет собой геометричес­кое место концов вектора 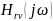, соответствующих изменению частоты

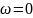
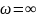(рис.2) На годографе указывают точки, со­ответствующие некоторым значениям частоты и стрелкой показы­вают направление перемещения конца вектора 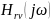при увеличении частоты. Как видно из рисунка, годограф КЧХ позволяет одновремен­но судить как об АЧХ и ФЧХ, так и о зависимости вещественной составляющих КЧХ от частоты. Годограф КЧХ иногда называют амплитудно-фазовой характеристикой цепи. Комплексные частотные характеристики цепи делятся на входные и передаточные. Когда отклик и внешнее воздействие рассматриваются на одних и тех же зажимах цепи (см. рис.1, а), КЧХ называется входной

Рис.2. Годограф комплексной ча­стотной характеристики цепи.

Если отклик и внеш­нее воздействие задаются на раз­ных зажимах цепи (см. рис.1, б), КЧХ называется передаточ­ной. Различают два вида вход­ных и четыре вида передаточных характеристик. Если внешнее воздействие на цепь является током 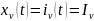, а реакция - напряжения то КЧХ цепи представляет собой комплексное входное сопротивление цепи относительно зажимов v — v'

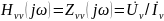
К входным характеристикам цепи относится также комплексная входная проводимость

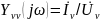
При этом внешнем воздействии – напряжение 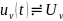, а реакция – ток

К передаточным характеристикам цепи относятся: комплексный коэффициент передачи по напряжению

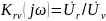
комплексный коэффициент передачи по току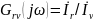

комплексное передаточное сопротивление

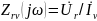
и комплексная передаточная проводимость

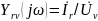
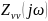Очевидно, что комплексное входное сопротивление и комп­лексное передаточное сопротивление 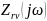имеют размерность со­противления, комплексная входная проводимость и комп­лексная передаточная проводимость — размерность проводимости.

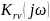Комплексные коэффициенты передачи по току и напряжению являются безразмерными величинами. В дальнейшем будет показано, что КЧХ линейных цепей не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой цепи и параметрами входящих в нее элементов.

Знание КЧХ позволяет определить реакцию цепи 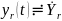на заданное гармоническое воздействие

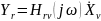
В общем случае каждая линейная цепь характеризуется большим числом комплексных частотных характеристик, так как любая из рас­смотренных разновидностей КЧХ может быть определена для раз­личных сочетаний пар входных и выходных зажимов и при различ­ных значениях сопротивлений нагрузки.