Решение:

1. Находим коэффициенты A_h=80 А_kh=12 при ф= m_ф=33,5^о согласно рис. 5.4.

2. вычисляем коэффициенты k1, k2, k3, по формулам (5.33а)

k₁= k₂=

k₃=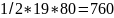

Коэффициент η=57,3 при определении к1 введён для перевода производной A_kh по градусам в производную по радианам.

3. Определяем числовые характеристики фактора Y1 (несущей способности основания) по формулам (5.33):

m_Y1= D_Y1=

μ_3Y1=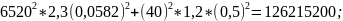

μ_4Y2=(6520)²*4,58(0,0582)²+(40²*3,44(0,5)²+3(760)⁴*(0,05)⁴+6(6520*40*0,0582*0,5)²+(6520*760*0,0582*0,05)²+(40*760*0,5)²=9710061*10⁴

3. Определяем числовые характеристики фактора Y2 (внешнего давления) по формулам (5.26а):

m_Y3=600; D_Y3=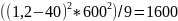

3. Определяем числовые характеристики совокупного фактора Y по формулам (5.30а):

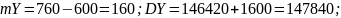
σ_Y= = ; μ_3Y=μ_3Y1=

μ_4Y=

1/υ_γ=m_γ/σ_γ= A=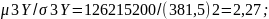

E_Y=μ_4Y/σ⁴_Y-3 =

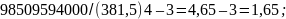
По таблице приложения 1 и ПЗ [56] находим:

Ф_z(z = 1/υ_Y= 0,42) = 0,3255; φ₀⁽²⁾(1/υ_Y=0,42) = - 0,3008;

φ₀⁽³⁾(1/υ_Y=0,42) = 0,4332.

Определяем расчётный уровень надёжности по второй формуле (3.28):

H_p=

Находим коэффициент запаса в общепринятом его понимании по формуле (3.30):

k_за=m_Y1/m_Y2= 760/600 = 1,27;

В рассмотренном случае вероятностному уровню надёжности =0,5788 соответствует =1,27. Для получения = =0,995 необходимого при всех прочих равных условиях иметь значение

При этом

;

.

Задача №7.

Расчетная осадка S однородного грунтового основания определяется 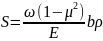, Формулой где - коэффициент бокового расширения;

- коэффициент, зависящий от формы штампа в плане; b- меньший размер площади штампа; E- модуль деформации грунтов основания; - давление штампа на основание. Все входящие в формулу (2.107) величины, строго говоря, являются случайными и практически независимыми друг от друга, за исключением коэффициента , который может быть принят практически постоянным д штампа данной формы.

Требуется определить характеристики S как функции случайных аргументов , E, b и , если числовые характеристики последних (m, D, и ) известны на основе обработки опытных данных.

Решение.

1. Для преемственности дальнейших выкладок с предыдущим изложением примем обозначения: 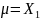, b= , , E= , ,

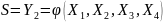С учетом этих обозначений формулу (2.107) можно представить в виде:

2. В соответствии с первой из формул (2.106) математическое ожидание осадки S= Y2 определится через математические ожидания mXj из выражения:

3. Находим первые производные функции Y2 по случайным аргументам:

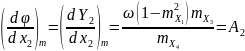
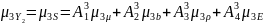
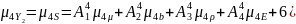
Определяем центральные моменты функции Y2 в соответствии с формулами (2.106) при известных, стоящих в правой части числовых характеристиках случайных аргументов ( , , , ):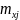

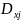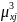В этих формулах при использовании первоначальных обозначений

; ; ;

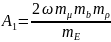Математические ожидания коэффициента бокового расширения меньшего размера площади подошвы фундамента b, удельного давления на грунтовое основание и модуля деформации E; - дисперсии перечисленных случайных величин;

• Третьи и четвертые центральные моменты перечисленных случайных мест величин, входящие в правую часть формулы (2.107)

Рассмотрение структуры формул (2.106) и полученных на их основе соотношений конкретном примере для числовых характеристик функций случайных величин позволяет видеть, что в соответствии с ними можно определить не только совокупные числовые характеристики функции по числовым характеристикам входящий в правую часть случайных величин, но и, что особенно важно, оценить удельную значимость влияния числовых характеристик каждой из случайных величин правой части на определяемую числовую характеристику функции.

Последнее обстоятельство имеет большое значение в практических инженерных расчетах, так как дает возможность, при необходимости, пренебрегать ролью второстепенных факторов и выделять главные определяющие факторы. При этом в стадии проектирования, возведения и эксплуатации грунтовых оснований сооружений представляется возможным обращать внимание на контроль над соблюдением требуемых пределов в изменении величин, таких, например, как величина деформаций и несущая способность грунтовых оснований.

Для оценки погрешностей в определении числовых характеристик ряда нелинейных функций методом линеаризации были произведены многочисленные расчеты с оставлением в разложении функции в ряд Тэйлора не только первых, но и вторых (квадратичных) членов.

Результаты расчетов показали:

а) в случае наличия даже существенной нелинейности и при значительном разбросе (рассеянии) случайных величин с дисперсиями, достигающими 20% от математических ожиданий, величины ошибок при нахождении математического ожидания, дисперсии центральных моментов третьего и четвертого порядков функции случайных величин не превосходят при использовании метода линеаризации 3÷ 5%;

б) расчетные зависимости, применяемые при проектировании грунтовых оснований и связанные с определением их несущей способности и деформаций как функций случайных аргументов будет практически всегда обеспечивать точность получения результатов, не меньшую чем 3-5%.

Задача №8

Опорный раскос стропильной фермы выполнен из двух уголков 160×100×10 из стали с расчетным сопротивлением 250 МПа. Расчетная длина стержня l=2,3 м. Требуется определить, выдержит ли этот стержень расчетное усилие N=550 кН. По сортаменту уголок 160×100×10 имеет следующие характеристики: площадь сечения А=25,3 см² , момент инерции I_x= 667 см⁴ и радиус инерции i_x=5,13 см.

Решение:

Определим гибкость стержня λ_x:

λ_x=l_x/i_x=230/5.13=44.8

где l_x- расчетная длина раскоса.

При этой гибкости коэффициент продольного изгиба φ=0,4.

Напряжение в стержне σ: σ= N/φA=550/10.12=54.3 кН/см²=543 МПа

543МПа > 250 МПа

Напряжение в стержне больше расчетного сопротивления, следовательно, опорный раскос перенапряжен; требуется его усиление.