МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

Факультет: Факультет очного и дополнительного образования

Кафедра: строительного производства и инженерные конструкции

Направление / специальность: Строительство

Профиль / специализация: Промышленное и гражданское строительство

Контрольная работа

по дисциплине «Безопасность зданий и сооружений»

Выполнил: , группа 3514

Проверил:          В.Х. Рыженко

Благовещенск, 2017

Задача №1.

Условие (3,9) расчета грунтового основания при предельном состоянии по несущей способности ( Если принять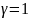 ) имеет вид:

N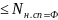

В принятых в настоящем параграфе дополнительных обозначениях это условие может быть записано следующим образом;

(3.35)

В результате испытаний при статистической обработке полученных данных, а также расчетами по определению числовых характеристик величин установлены для конкретных условий следующие соотношения:

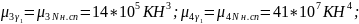
Определить надежность грунтового основания Н.

Решение:

Определяем коэффициент запаса по формуле(3,30):

Вычисляем коэффициенты вариации из выражения(3,32):

Находим обратную величину коэффициента вариации случайной величины Y из соотношения (3,33):

Определяем величины центральных моментов по формуле(3,29):

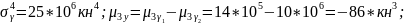
По таблице приложения 1 и таблице ПЗ (56) определяем значение ФZ и функции ( z ) при

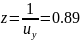
Вычисляем расчетную надежность по формуле (3,27)или (3,28) для первой ) предельного состояния:

(3.36)

Таким образом, при заданных условиях грунтовое основание имеет первому предельному состоянию надежность =0,87.

Если в первой задаче при всех прочих равных условиях значение увеличится с 1,25 до 2 путем упрочнению грунтового основания, то, как показывают расчеты, уровень надежности повысится до н=

Аналогичным образом могут быть решены задачи по определению уровня надежности для грунтовых оснований по второму предельному состоянию.

В этом случае расчет надежности происходит в соответствии условием (3,11) предельного состояния по деформациям.

С использованием понятий факторов Y, y1 y2 соотношение (3,11) принимает вид:

(3.36)

Величина в соотношении (3.36) является постоянной величиной, а значение = - случайной.

Как показывают численные расчеты по формулам(3.26) ,(3.27) ,(3.28), влияние членов расчетных соотношений для определения надежности, зависящих от третьего и четвертого центрального моментов, обычно не превосходит нескольких процентов. Это влияние тем меньше , чем больше коэффициент запаса и чем меньше коэффициент вариации физико- механических свойств грунтовых оснований .Поэтому для грубых прикидочных расчетов можно использовать указанные формулы без учета третьего и четвертого членов в этом случае.

(3.37)

Использование последней формулы равносильно принятию для совокупного фактора Y нормального закона распределения.

Такой грубый подход к определению надежности становится недопустимым, если речь идет о технико-экономической оценке принимаемых решений в зависимости от надежности.

Все дело в том, что повышение надежности даже на несколько процентов, как показывают расчеты, требует значительного увеличения коэффициента запаса, т.е. приводит к существенно менее экономичному решению. Из сказанного следует, что технико-экономическое обоснование применяемых решений в качестве промежуточной стадии целесообразно производить в зависимости от коэффициента запаса, так как эта задача более легка для решения, чем выявление технико-экономических показателей в зависимости от уровня надежности.

Учитывая что коэффициент запаса по формуле(3,34) непосредственно связан с уровнем надежности, в дальнейшем нетрудно определить и связь технико-экономических показателей. В связи этим может представить интерес зависимости коэффициента запаса от величины входящей в формулы надежности в качестве аргумента функции 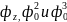( z ).Эта связя устанавливается из соотношения (3,33) при решении его относительно и имеет вид.

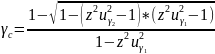(3.38) или

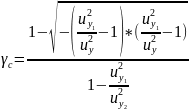(3.38а)

Рис 3.1. Зависимость уровня надежности от величины коэффициента запаса

График изменения уровня надежности в зависимости от показателя .

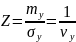и коэффициент запаса при

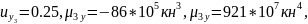
полученный на основе расчетов по формулам (3,34)и (3,38) соответственно, приведен на рис. 3.1.

Анализ формулы (3,33) и выведенного на ее основе соотношения (3,38) показывает что повышение ,а , следовательно и уровня надежности, наиболее целесообразно получать путем снижения коэффициента вариации <<внутреннего>> фактора грунтового основания ,т.е. повышение однородности грунтов. более подробно этот вопрос будет рассмотрен в гл. 4.

Задача №2

Имеются данные испытаний модуля деформаций двух соседних слоев грунта. Объем выборки для первого слоя п₁=11, для второго слоя п₂=11. Врезультате обработки исходных данных по формулам (4.1-4.3) найдено, что m_x1=T_E1=12 Мпа; m_x1=T_E114 Мпа; Ϭ^*_x1=Ϭ^*_E1= 1,6 Мпа.

Требуется установить, можно ли считать слои грунта однородными по модулю деформации.

Решение

Согласно (4.23) находим

σ_{(m*X1- m*X2)ф}= √

При Р=Ф(z) по приложению I находим z = 1,96.

Согласно (4.24)

(m_X1 – m_X2)_пред = 1.96 * 0.60 = 1.17Мпа;

фактическое значение

(m*_X1 – m*_X2)ф = 14 – 12 = 2 Мпа.

Так как 2МПа>1.17 Мпа. то расхождение слоев по деформативности следует считать весьма существенным. Таким образом, рассматриваемые слои являются неоднородными и по этому показателю их следует считать самостоятельными.

Первый метод оценки однородности слоев является наиболее простым. С него и следует начинать.

2. Оценка однородности слоев грунта путем проверки гипотезы об однородности дисперсий (прием Бартлета).

В качестве критерия принимается величина (Gi)_ф равная

(Gi)ф =

где i – номер выработки; k- число выработок; D/D*….D*-дисперсии выборок;

D*_max- максимальная дисперсия для рассматриваемых выборок.

При статической однородности выборок, т.е. при однородных слоях грунта, по показателю G, значение (G)_ф должно быть меньше предельного (G)_пред, который принимают по табл.8 приложения 43 при заданном уровне значимости q=1-P и число степеней свободы(л-1).

Задача № 3

Исходные данные те же, что и в предыдущем примере; число выработок k=2.

Решение

D*_X1 = D*_E1 = (𝛔*_X1)² = 1.44 Мпа². D*_X1 = D*_E1 = (𝛔*_X1)² = 2.56 Мпа².

Согласно(4.25) вычисляем

(Gi)_ф =

По табл. 8 приложения 43 при (n-1)=11-1=10 и k=2. q=0.05 и P=0.95 находим (Gi)_пред=0,788. Так как (Gi)_ф<(Gi)_пред то с точки зрения изменчивости (разброса) модулей деформации рассматриваемые слои являются однородными. Однако, если учесть также результаты решения примера по первому методу, то в целом рассматриваемые слои следует считать самостоятельными ввиду большого различия их статических математических ожиданий. Этот последний показатель существеннее в отношении влияния на величину деформаций основания, чем величина дисперсии.

Прием Бартлета является упрощенным и применим при сомнительности результата, полученного по первому методу для случая одинакового обьема выборок. При разном объеме выборок и сомнительности результата оценки однородности слоев по первому методу используя третий метод.

3. Оценка однородности слоев грунта путем проверки гипотезы об однородности дисперсии по критерию Фишера.

В качестве критерия сопоставляемых выборок принимается фактическая величина которой

F_ф=

где D_max,D_min- наибольшая и наименьшая из статистических дисперсий сравниваемых слоев(выборок) по данному показателю.

По специальной табл.6 приложения 43 по заданному уровню значимости q=1-P

в зависимости от K1=k1 – 1 и K2= k2-1( здесь n1 и n2 – объемы выборок) определяется Fпред. Если то различие в дисперсиях Dmax* u Dmin* считается незначительным и считается однородными в отношении разброса показателя; В противоположном случае слои – неоднородные.

Задача №4

По данным испытаний на сдвиг для двух сопоставляемых слоев получены две выборки для углов внутреннего трения φ песчаных грунтов. Наибольшее значение дисперсии (D^*1φ) = (D^*φ)max = (6^o)2 оказалось в первой выборке, наименьшее (D^*φ2) = (D^*φ)min = (3.5^o)2 – во второй ( для второго слоя). Необходимо проверить гипотезу о равенстве дисперсий выборок при объемах выборок n1 = 25 и n2 =15 и уровне значимости q= 0.05%(P= 0.95)

Решение:

Согласно (4,26) величина F_ф =

По табл. 6 приложения 43 для K1= n1 – 1= 24 и K2= k2 – 1 = 14 и q= 5% находим F_пред = 2,35. Так как F_ф = 2.94 > F_пред = 2.35, то гипотеза о равенстве дисперсий угла внутреннего трения сопоставляемых слоев грунта противоречит опытным данным а, следовательно, в рассматриваемом смысле( в отношении разброса угла внутреннего трения), слои не могут считаться однородными.

4.Оценка однородности слоев по совокупности показателей свойств грунтов. Рассмотренные методы оценки однородности выборок из различных соседних слоев грунта обладают тем существенным недостатком, что однородность выборок исследуется лишь по отдельным показателям свойств грунта. Вследствие этого может оказаться, как мы видели в примерах расчета по первой и по второй методикам, что два соседних слоя грунта, однородные по одному из показателей, могут оказаться неоднородными по некоторым другим показателям. Поэтому в ряде случаев целесообразна оценка однородности слоев грунта по совокупности показателей. Такой метод разработан Д.А. Родионовым в качестве критерия при этом используется величина υф определяемая из соотношения:

υф=

где m – число показателей, привлекаемых для оценки однородности слоев грунта;

Y₂ = ѱ(X₁, X_2,X_3,X₄) =

2. В соответствии с первой из формул(2.106) математическое ожидание осадки S=Y2 определится через математическое ожидания mXJ из выражения

m_y2=

3. Находим первые производные функции Y2 по случайным аргументам:

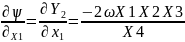; ( )_m = - = -A1; = =

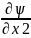)_m =( _m = =

(∂ѱ/∂x3)m =( ∂Y2/∂Y3)m = = ω(1-m_X1^2 ) m_X3)/m_X4 =A3;

∂ѱ/∂x4 = ∂Y2/∂x4 = -ω(1-X_(1 )^2)X2X3/X_4^2;

(∂ѱ/∂x4)m =( ∂Y2/∂Y4)m = = ω(1-m_X1^2 ) m_X3m_X2)/m_X4^2 = -A4;

= = ,

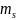μ_(4Y2 )=μ_4S=-A_1μ4μ^4+A_2^4 μ_4b + A_3^4 μ_4p-A_4^4 μ_(4E,);

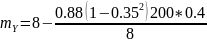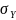
= 0.27; =3.25;

= = = 0.08; 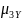= (0.9)^4 * 0.115 * 36^4 +6(0.038)^2*(0.9)^2 *25 *3.6^2=126.98.

Определим асимметрию и эксцесс У, используя формулы (3,28а)

По таблице приложения 1 и таблице П3 51 находи:

φ_z (z- -0.06) -0.0638; φ₀^2( - 0.08) = -0.3951.

Вычисляем по второй формуле(3,28) расчетный уровень надежности:

И_р-И = (1+ 0,0638) - 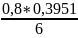= = 0,474;

Если принять за нормальный уровень надежности Н_н = 0,995, то, как видим расчетный уровень надежности Н_р = Н = 0,474 значительно меньше нормативного(Н_р = 0,474 <Н_н = 0,995). При подходе к расчету оснований по рекомендациям СНиПа для рассматриваемого случая расчетная величина осадки

S = 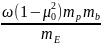= = 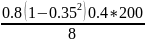7.73 см.

Таким образом S = 7.73см < S = 8см и система основание-фундамент считается надежной.

Из рассматриваемого случая очевиден принципиальный недостаток существующего подхода к оценке надежности систем основание-фундамент, не учитывающего прямым образом статистическую изменчивость показателей свойств грунтов и размеров подошвы фундаментов.

В случае для получения надежности, близкой к принятой нормативной, необходимо при заданных условиях нагружения (Тр=0,4Мпа) и размерах площади фундамента увеличить модуль деформации Те и снизить его изменчивость σ_Е, что приведет в конечном счете к повышению величины =

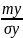
непосредственно входящей в соотношения для уровня надежности. Повышение значения до 1,8 дает уровень надежности при всех прочих равных условиях Н=0,995 = Нн.

Аналогичным образом по формулам может быть определен уровень надежности для предельного состояния по деформациям и случаи слоистых оснований, когда при расчете конечных осадок используются методы эквивалентного слоя и послойного суммирования.

Для определения уровня надежности основания по несущей способности используют формулы применительно к различным случаям определения несущей способности основания.