Задание 1. Задачи на закрепление материала

Статистический ряд задан таблицей. Требуется:

а) построить гистограмму относительных частот;

б) перейти к вариантам и построить полигон относительных частот;

в) записать эмпирическую функцию распределения и построить ее график;

г) найти точечные оценки , , ;

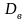1.	(–6; –4) (–4; –2) (–2; 0) (0; 2) (2; 4) (4; 6) 2 6 17 18 4 3
2.	(0; 2) (2; 4) (4; 6) (6; 8) (8; 10) (10; 12) 1 3 19 21 4 2
3.	(–4; –2) (–2; 0) (0; 2) (2; 4) (4; 6) (6; 8) 3 8 14 15 9 1
4.	(–2; 0) (0; 2) (2; 4) (4; 6) (6; 8) (8; 10) 1 4 20 19 4 2

Тема лекции: Интервальные оценки параметров распределения

Определение: Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Так как любая оценка есть некоторое приближение оцениваемой величины a, то возникает вопрос об оценке точности данного приближения, т. е. можно ли утверждать, что для некоторого .

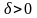Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству . Можно лишь говорить о вероятности  наступления события, заключающегося в том, что мы получили оценку с точностью 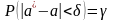: . Эта вероятность называется доверительной вероятностью (или надежностью), а интервал – доверительным интервалом. Вероятность того, что интервал 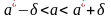заключает в себе неизвестный параметр a, равна . Обычно надежность выбирают близкой к единице (0,95; 0,99; 0,999).

1. Интервальная оценка математического ожидания нормального распределения

Если случайная величина распределена нормально и среднее квадратическое отклонение  известно, то доверительный интервал для оценки математического ожидания a

, (1)

где n – объем выборки, t находится из равенства 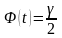по таблице значений функции Лапласа .

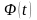Если  неизвестно, то в формуле (1) оно заменяется на исправленное среднее квадратическое отклонение S, t заменяется на  , которое находится по таблице (приложение )

. (2)