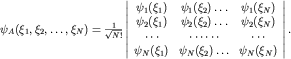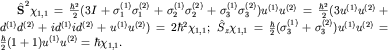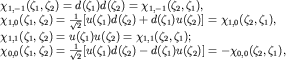Паули принципі

Фермиондар жүйесі үшін антисиметриялық функцияны аламыз. Оны Слэтер (J. Slater, 1929) анықтамасы арқылы жазуға болады:

Мұнда N! нормалау коэфициенті N бөлшектер арасындағы орын ауыстыру санын енгізеді. және функциясының интерпретациясы мынадай функциясы (“дұрыс емес”) жүйесінің күйін сипаттайды, мұндай бірінші бөлшек бірінші күйде , ал 2- бөлшек күйінде болады. Дұрыс функцияда N бөлшектер N бірбөлшекті күйді толтырады, онда қандай бір бөлшектің қандай күйде тұрғанын анықтау мүмкін емес, бұл теңдік бөлшектердің үздіксіз принципімен келісетінін көрсетеді. Егер олардағы бірбөлшекті функциялар бірдей болса, онда күштей белгілі анықтауыштың қасиеті бірдей. Бұл ондай күйдің болмайтынын көрсетеді, сөтіп ол электрондар үшін құрылған Паули принципіне әкеледі: Бір және сол бір бөлшекті күйден бір фермионнан артық болмауы мүмкін емес. Паули принципі- антисиметриялық толқындық функцияның негізі, сондықтан ол тек фермиондар үшін дұрыс болады.

Екі электрондардың жүйесі

Екі электрондардың жүйесінің толқындық функциясы антисиметриялық шарттарын қанағаттандырады:

Біріншіден жүйенің спин операторын табайық:

жүйесінің спиндік кеңістігіндегі жеке электрондардың кеңістік спинінің индексін нөмірлейді. Әр бір кеңістіктей C² базистік векторға ие:

Олар және операторларының меншікті векторы болады. C⁴ кеңістігінде базис ретінде 4 векторды таңдауға болады.

u(1)u(2), d(1)d(2), u(1)d(2), d(1)u(2).

Меншікті толық спинінің квадраттық операторының векторы және z осінің проекциясынан құралған жаңа базис таңдау ыңғайлы:

Ескерту: Жүйенің екі бөлшекті операторының қысқартылған жазбасын пайдаланамыз. Спиннің проекция операторы мынадай:

Берілген базистің түрін тексеру оңай:

Векторлар, индекстер мәні былай:

Тікелей тексеру формула көмегімен жүргізіледі:

Мысалы,

Одан шығатыны,

. Теориялық көзқарас бойынша біз дәлелдедік:

Кеңістіктегі D_J 2J+1 өлшемді базис векторы мына түрде болады:

Олар момент операторының меншікті векторы және . C(j₁j₂JM|j₁j₂m₁m₂) коэфициенттері- Клебша-Гордан коэффициенті деп аталады. Электрондар және үшін дискретті спинді айнымалыларды енгізе отырып, табылған базистік векторларды екі айнымалының функциясы түрінде жазамыз:

Мұнда үш симетриялық функция D₁ кеңістігінде базис құрайды, ал антисиметриялық функция D₀ кеңістікті құрайды.

Гелий атомы

Екі электронның және ең зарядталған ядродан Z=2 құралған, ⁴₂He гелий атомының спектрларының жалпы құрылымын талдау үшін жоғарыда алынған нәтижелерді қолданамыз.

мұндағы r₁₂=|r₁-r₂| - электрондар арасындағы арақашықтықтың спиндік өзара әсерлесу релятивистік емес жақындауда ескерілмейтінін белгілейміз. Шредингер теңдеуінің стационар шешімін

Алдыңғы бөлімде тапқандай, базистің спиндік функцияларын тарату бойынша табуға болады:

Спиндік функциялардың симетриялық қасиеті мен антисиметриялық толық функциядан шығатыны, координаттық функциялар анықталған симетрияға ие:

Яғни H_A(H_S) кеңістігінде жатады L²(R⁶) кеңістік мұндағы S=1 (S=0). Бұл функциялар Шредингердің теңдеуін қанағаттандырады, φ сияқты :

Симметриялық және антисимметриялық функциялар әр түрлі меншікті мәнге жатады. Осылай, спиндік гамильтонианға өзара әсерін ескермей- ақ гелий атомының энергия теңдеуі толық спиннен S тәуелді. Бұл тәуелділік координаталық толқындық функцияның симетриялық қасиетіне негізделген және теңдік принциптің нәтижесі. Гелий атомының негізгі жағдайына симетриялық функция мен спин S=0 жауап беретінін дәлелдеуге болады.

Әр түрлі спиндердің фотон шығаруы мен жұтуы арасындағы күйлерінің ауысу ықтималдылығы аз. Дипольдік жуықтауда ауысу ықтималдылығы нөлге айналады:

Сондықтан, гелий атомының сәулелену спектрі парагелий (S=0) мен ортогелий (S=1) гелидің екі түрі бар болуына мысал бола алады. Ортогелий энергиясының теңдігі спиндік сай бойынша үш реттік мәнге ие. Толық спиннің проекциясы S_z(2S+1=3).

Әдебиеттер: негізгі [1-12], қосымша [1-5].