
- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
Мұнда спектралдық кеңістік пайдаланылады.
Жоғарыда айтқандай, бұл үш үлестіруден тұрады:
1)
Ферми-Дирак
үлестіруі.
Бұл бөлшектердің антисиметриялық күйін
қарастырады. Квантық механикадағы
антисиметрия толқындық функциямен
сипатталады. Мысалы, бұған электрон
жатады. - спиндер.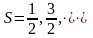
2)
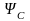 -
симметрия толқындық функциямен
сипатталады. Бұл Бозе-Энштейн үлестіруі
S=0,1,2,…
-
симметрия толқындық функциямен
сипатталады. Бұл Бозе-Энштейн үлестіруі
S=0,1,2,…
3) Планк үлестіруі.
Бұл сәуле шығару, жұту, т.б. қарастырылады. Солардың үлеструі.
1-ші үлестіру бойынша термодинамикалық шамалар өзара коммутативті емес (орын ауыстыруға болмайды). Мұнда термодинамикалық шамалардың барлығы операторлық түрде қарастырылады.
2-ші үлестіруде керісінше, яғни коммутативті болады.
3-ші үлестіру абсолютті қара дененің сәулеленуінің теориясын құрайды.
Ферми - Дирак үлестіруі.
Ферми - Дирак үлестіруін Паулидің принципіне сүйене отырып табуға болады. Мұнда бір күйдегі n - бөлшектің саны не 0-ге, не 1-ге тең болады.
n=0 , 1
Бұл үшін егер де . Сол сияқты
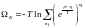 (1),
себебі
(1),
себебі
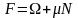 бұдан
бұдан 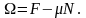
Ферми-Дирак
үлестіруі үшін
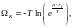 себебі n=
себебі n=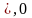 Паули
принципі.
Паули
принципі.
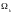 -термодинамикалық
потенциал, μ-химиялық потенциал. Біз
білеміз:
-термодинамикалық
потенциал, μ-химиялық потенциал. Біз
білеміз: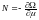 ,
онда орта мәні
,
онда орта мәні
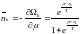 немесе
немесе
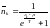 (2)
(2)
Ферми - Дирак үлестіруі шығады:
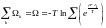
Бозе-Эйнштейна үлестіруі.
Бұл
үлестіру симметриялық
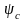 бөлшектерге онда
бөлшектерге онда
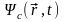 ,
симметриялық толқындық функция. Ьұнда
n=0,1,2, ...
,
симметриялық толқындық функция. Ьұнда
n=0,1,2, ...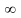
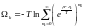 (4)
(4)
Геометриялық
прогрессия орындалу үшін қатар сәйкестік
керекті турде μ<1, яғни химиялық
потенциал кері түрде болуы керек: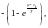
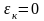 -де де орындау керек, онда
-де де орындау керек, онда
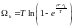 (5)
(5)
Ал
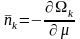 ,
одан
,
одан
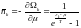 (6)
(6)
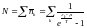 (6’)
(6’)
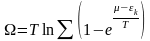 (7)
(7)
Ал
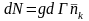 ,
,
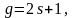 s
– спин.
s
– спин.
Бозе-Эйнштейнің (4-6) үлестіруі болады.
Әдебиеттер: негізгі және қосымша.
12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
Жоғарыда қарастырғандай (2) және (6) ± таңбалармен өзгеше.
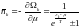 (8)
(8)
 ,
себебі
,
себебі
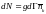
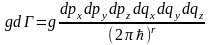
бұнда g=2S+1, S- элементарлы бөлшектер спині, dГ- спектрлық көлем, статистикалық салмақ
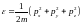 ,
,
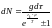 (9)
(9)
немесе
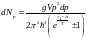 (10)
(10)
Олай
болса
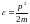 ,
,
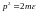 ,
,
![]() ,
сонда
,
сонда
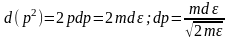
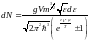 (11)
(11)
Термодинамикалық потенциалға ауыссақ Ω:
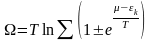 (7)
(7)
Оны табуға болады, ол (қосындыдан интегралдауға ауысу әдісі)
 (12)
(12)
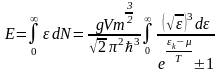
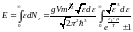 (13)
(13)
Егер Ω=-PV, онда
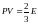 , (14)
, (14)
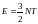
PV=NT (15) - Клапейрон теңдеуі.
Егер
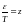 ,
онда (12) теңдеу:
,
онда (12) теңдеу:
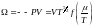 (16)
(16)
Аддитивтіктең S=-N ln P+NCp ln T=const. Одан
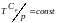 .
(17)
.
(17)
Егер
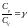 ,
онда
,
онда
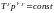 (18)
(18)
PV=NT
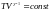 (19)
(19)
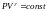 (20)
(20)
Біздін жағыдайда:
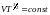 (21)
(21)
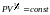 (22)
(22)
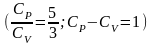 идеал
газбен сәйкес келмейді.
идеал
газбен сәйкес келмейді.
Әдебиеттер: негізгі және қосымша.
13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
Ол Ферми статистикасына бағынады. Т=0 болған кезде осындай электронды газ толығымен сиретілген газ деп атылады.
Паульдің принципы бойынша бір электрон ең кіші немесе ең үлкен q0 және олардың p,p+dp интервалындағы ілгерлемелі қозғалысынынаң тұрады және де кванттық күйлер санымен анықталады:
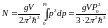 (1)
(1)
Себебі
мұнда p0-
ең үлкен импульс. Осыдан:
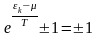
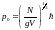 және
және
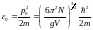 (2)
(2)
Т=0
болған кезде Ферми статистикасынаң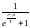 1,
немесе 0 тең мәнге ие болады.
1,
немесе 0 тең мәнге ие болады.
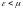 болғанда
-1
болғанда
-1
2)
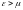 болғанда - 0.
болғанда - 0.
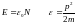 ,
онда
,
онда
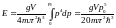 .
.
,
сонда
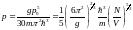 .
.
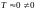 .
.
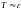 болғанда,
онда –сиретілген
газ
болғанда,
онда –сиретілген
газ
Сиретілген газ жағдайында Сp=CV=С және
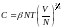 ,
онда
,
онда
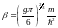 .
.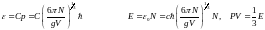
Қара сәулелену.
Фотондық
газ Бозе-Эйнштейнің статистикасына
бағынады. Фотондар өзара әсерлеспейді.
Ортада бұл орындалмауы мүмкін. Бірақта,
еркін энергия аз деп болжасақ яғни
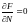 ,
онда
,
онда
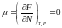 екенін табуға болады және Бозе-Эйнштейн
үлестіруінен:
екенін табуға болады және Бозе-Эйнштейн
үлестіруінен:
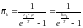 (1)
(1)
мұндағы
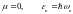 ,
ал
,
ал
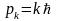 ,
,
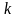 -
толқындық
вектор.
-
толқындық
вектор.
Берілген үлестіру Планк үлестіруі деп аталады.
Осы кезде
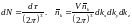
 (2)
(2)
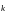 -
толқындық вектор және
-
толқындық вектор және
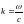 ,
онда (2) теңдеу мына турде жазылады:
,
онда (2) теңдеу мына турде жазылады:
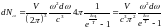 және
және
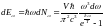 (3)
(3)
Белгілі Планк теңдеуі.
Әдебиеттер: негізгі және қосымша.
