
- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
Егер де газды құрап тұрған молекулалар өзара әлсіз әсерлесетін болса, бұл әсерді ескермеуге болады. Мұндай газдарды идеал газдар дейді. Бұл ұғымды алғаш рет термодинамикаға енгізген Больцман. Сондықтан мұндай газдарды Больцманның идеал газдары дейді.
Егер де молекуланың күй деңгейлерінің энергиясын Ек деп белгілесек, к- кванттық сандар жиынтығы.
Еn - молекуланың энергиясының жиынтығы. Осыны есептей келе Больцман Гиббстің үлестіруін пайдалана отырып, к күйдегі сан деген ұғым енгізді. Оның орташа шамасы nk деп белгілесек, ол
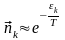
деген заңдылық ұсынды. Немесе
 (1)
(1)
(1)-ші теңдеуді Больцманның үлестіруі дейді.
Больцман үлестіруі (идеал газдар үшін)
- ші теңдеуді пайдалана отырып, Гиббстің үлестіруіндегі
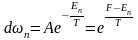 бұнда
бұнда
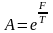 ,
дәлелдейік
,
дәлелдейік
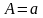 деп
алатын
болсақ,,
онда
деп
алатын
болсақ,,
онда
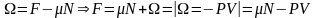
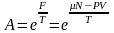
Егер де А=а дейтін болсақ, бұл бір деңгейдегі N=1-ге тең, идеал газ үшін P=o осыны ескерсек,
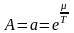 (2)
(2)
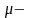 химиялык
потенциал.
химиялык
потенциал.
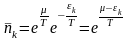
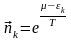 (3)
(3)
(3)- идеал газ үшін Больцман үлестіруі. Бұл квантталған күй үшін, спектралдық геометрия үшін алынған теңдеу. Егер де (3) - ші теңдеуді фазалық кеңістікте қарастыратын болсақ, онда ол былай жазылады:
 (4)
(4)
Бізге
белгілі
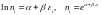 (5)
(5)
(5)
- ші
және
(3) - ші
теңдеулерді
салыстырсақ,
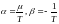 (6)
(6)
Больцман үлестіруінің Максвелл үлестіруінен айырмашылығы, Больцман үлестіруінде ықтималдылықтың орнына орта сан деген ұғым енгізіледі. Осы екі үлестірудің арасында ұқсастық бар, ол байланысты:
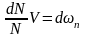 (7)
(7)
(7) - теңдеу статистикалық ықтималдылық пен термодинамикалық жүйеге кіретін молекулалардың бір деңгейдегі санының өзгерісі, сол термодинамикалық жүйені құрып тұрған көлемінің статистикалық ықтималдылықпен байланысының теңдеуі. dN-сан өзгерісі, Ν-жалпы сан, V-көлем.
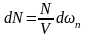 (8)
(8)
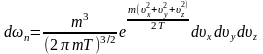 (9)
(9)
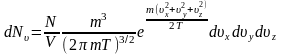 (10)
(10)
(10)-теңдеуді Больцманның идеал газдар үшін Максвеллдің үлестіруі дейді. Бұл теңдеудің ерекшелігі (10)-шы теңдеуді жылдамдық бойынша интегралдау арқылы Больцманның идеал газындағы молекуланың ыдыстың қабырғасына соғылу санын есептеп табуға болады.
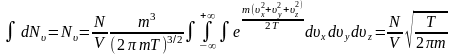
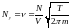 (11)
(11)
(11)- теңдеуді Больцманның идеал газындағы молекуланың ыдыстың қабырғасына соғысу саны дейді.
Тепе-теңсіздік күйдегі Больцманның идеал газдары.
Бұл құбылысты энтропия және бос энергияның теңдеулерін пайдалана отырып, қарастыруға болады.
а)
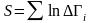 (1)
(1)
S-энтропия , Гі-статистикалық салмақ.
Больцман статистикалық салмақты термодинамикалық жүйеге кіретін молекулалардың санымен, соның статистикасымен байланыстырған. Сондықтан Гі-ді статистикалық салмақ дейді. Егер де топтағы бөлшектердің күй санын Ģі деп белгілесек, Nі! - орын ауыстыру ықтималдылығының үлестіру саны деп белгілесек, сол уақытта
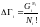 (2) Gi>>Ni,
(2) Gi>>Ni,
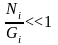
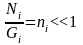
теңдеуді Больцманның күй теңдеуі немесе статистикалық салмақтың молекулалар санына байланысы дейді.
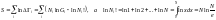 (3)-(4)
(3)-(4)
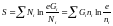 ,
мұнда
,
мұнда 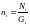 . (5)
. (5)
(5) теңдеуді энтропияның орта санымен байланысының теңдеуі дейді.
б) Больцманның идеал газдары үшін бос энергия;
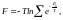 (6)
(6)
(6) теңдеуден деңгейлік күй санына көшу үшін кванттық механикадағы мына теңдеуді пайдаланамыз:
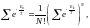 (7)
(7)
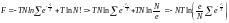 .
. 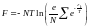 (8)
(8)
(8) теңдеу бос энергияның Больцманның идеал газының температурасы мен соған кіретін молекуланың санына тәуелді екенін көрсетеді. Осы теңдеуді пайдалана отырып, Больцманның идеал газының теңдеулерін табуға болады.
Әдебиеттер: негізгі және қосымша.
10 тақырып. Больцманның идеал газдар үшін теңдеулері.
Больцманның идеал газында молекулар екі түрлі қозғалыста болады.
1) Ілгерлемелі қозғалыс.
2) Айналмалы қозғалыс.
Егер жалпы энергияны екі қозғалыстын қосындысы ретінде алсақ (1) теңдеудің мәнін өткен тақырыптағы теңдеуге қойып, квантық механиканың төмеңгі теңдеу пайда болады.
Теңдеулерді ескеріп отыратын болсақ және импульс бойынша 3-тік интегралды шешсек, онда
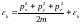 (1)
(1)
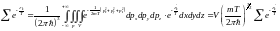 (2)
(2)
(2)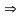 (8)
(8)
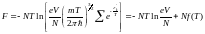 (3)
(3)
онда V=dxdydz, f(T)- T функциясы. Онда газдын кысымы, егер де F-тың орнына 3-ші теңдеудегі мәнің қоятын болсақ,мынадай теңдеу шығады:
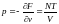 ,
,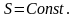 (4)
(4)
PV=NT (5) PV=NkT (6)
3-ші теңдеуіміз идеал газдардың жалпы теңдеуі дейді.
5-ші, 6-ші теңдеулерді Больцманның И.Г. негізгі теңдеулер деп аталады.
1) E=F+TS
2) W=E+PV=E- , =-PV
3) Ф=F+PV
4) =F-Ф=-PV
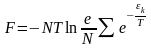
Осы
теңдеудегі F-тің
санға байланысты , Т-ға
байланысты және Больцманның үлестіруіне
байланысты мәнін қойып энергия, жылу
энергиясы, Гельмгольц функциясы, Гиббс
функциясының
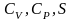 өте
оңай табуға болады.
өте
оңай табуға болады.
1. Бұл 3 үлестіруді (Гиббс, Больцман, Максвелл) одан шыққан жалпы теңдеулер тек қана оның ішінде идеал газдар үшін алынған теңдеулерді Т-ның шамасы үлкен болғанда ғана пайдаланады.
Егерде температура төмен болса бұл 3 үлестіру қолданылмайды және бұл 3 үлестіру жалпы классикалық тұрғыда ғана қарастырылады.
Егерде термодинамикалық жүйенің температурасы төмен болса оған басқа үлестірулер қолданылады. Мысалы: Ферми-Дирак, Бозе-Энштейн, Планк үлестірулері.
Бұл үлестірулер (статистикалар ) спектралдық кеңістік пен спектралдық геометрия тұрғысында термодинамикалық жүйені зерттейді немесе мұны кванттық статистика дейді. Сонымен термодинамиканың кванттық статистикасы спектралдық геометрияның заңдылықтарына сүйенеді.
Әдебиеттер: негізгі және қосымша.
