
- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
7 Тақырып. Термодинамикалық потенциалдың
бөлшектерінің санына байланыстылығы.
Термодинамикалық потенциалдың бөлшектерінің санына байланыстылығын химиялық потенциал арқылы сипаттауға болады. Осыны көрсету үшін (1)-ші топтағы теңдеулерді төмендегідей түрде жазуға болады:
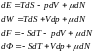
-химиялық потенциал.
Химиялық потенциал дегеніміз - химиялық реакция жүрген кезде термодинамикалық жүйе энергия бөліп шығарады және жұтады.
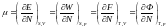 (1)
(1)
мысалы:
 (2)
(2)
Химиялық потенциал дегенді енгізген - Гиббс.
Химиялық потенциалдың еркешелігі қанша уақыт жүреді, ол жүре ме, жүру уақытын көрсететін шама. Осыған байланысты химиялық потенциалдың сипаттамасын көрсету үшін тағы да термодинамикалық потенциал деген ұғым енгіземіз. Ол потенциалды Гиббстің потенциалы немесе Гиббстің функциясы деп атайды.
Әдебиеттер: негізгі және қосымша.
8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
Гиббстің функциясын табу үшін бос энергияның (dF) теңдеуін пайдаланамыз.
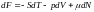

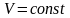 болса
болса
 не
болмаса
не
болмаса
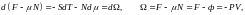
Осыдан:
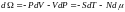

N=
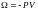
(1), (2)-Гиббстің энергиясы немесе термодинамикалық потециал деп аталады. Бұл функция химиялық потенциал мен бөлшектің санына байланысты.
Егер өткен тақырыптағы (2)-ші теңдеуді пайдалансақ,
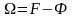 (3)
(3)
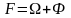 (4)
(4)
Гиббстің
потенциалы p-
қысым мен V-
көлемнің көбейтіндісінің кері өзгерісі
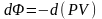 .
.
Бөлшектің санына байланысты екенін зерттеген кезде жылу сиымдылығы классикалық, кванттық тұрғыдан қарағанда екі түрлі мән береді. Оның себебі: бөлшектің санына байланысты, химиялық потенциалға байланысты. Ол алынған теңдеулерді әрі талдау, зерттеу үшін статистикалық үлестіру деген классикалық және кванттық тұрғыдағы 6 үлестіруді қарастыру керек.
Термодинамикада бұл 6 үлестіру былай деп аталады:
Гиббстің үлестіруі
Максвелдің үлестіруі
Больцман үлестіруі
Бұл 3 үлестіру температура жоғары болғанда, классикалық термодинамиканы қарастырғанда пайдаланылады.
Ферми-Дирак үлестіруі
Бозе-Эйнштейн үлестіруі
Планк үлестіруі
Бұлар термодинамикалық жүйенің температурасы төмен болғанда, кванттық тұрғыда қарастырғанда пайдаланылады.
Гиббстің үлестіруі.
Ол бүкіл термодинамиканың негізін құрайтын үлестіру, ал қалған 5-еуі оның салдарын құрайды. Термодинамикалық жүйе тепе-теңдік болғанда статистикалық матрица
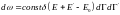 (1)
(1)
Еn- қарастырып отырған көлемнің бір бөлшегі, соның энергиясы, Е'- қалған бөлшектің энергиясы, E0- жалпы энергия.
dГ- бөлшектің статистикалық салмағы, dГ'- қалған бөлшектің статистикалық салмағы, dГn- бірлік , n-сан.
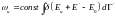


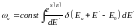
егер E’=E0-En онда:
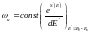 (2)
(2)
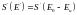 ,
бұнда
E0>>Eu,:
,
бұнда
E0>>Eu,:
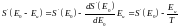 ,
,
(2) тендеуге қойғанда:
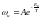 (3)
(3)
 ,
,
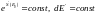 .
.
Бұл
теңдеуді
 функцияның
қасиетін
пайдалана
отырып
жаздық.
функцияның
қасиетін
пайдалана
отырып
жаздық.
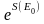 және
E'=const
баяу
өзгеретін
шама.
және
E'=const
баяу
өзгеретін
шама.
(3) - Гиббстің үлестіруі деп атайды.
(3)-тендеуден А коэффицентін табуға болады.
 (4)-нормалау
шартын
қарастыратын
болсақ
(4)-нормалау
шартын
қарастыратын
болсақ
 ;
;
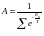 (5)
(5)
 (6)
(6)
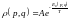 (7)
(7)
![]() (8)
(8)
Осы барлық теңдеуді Гиббстің үлестіруінің жалпы теңдеулері.
Термодинамикалық шамаларды жылдамдық арқылы сипаттауға болады. Оның үлестіруін жылдамдық үлестіруі арқылы құруға болады. Мұны құрған Максвелл болатын.
Максвеллдің үлестіруі.
Гиббстің үлестіруін (3)-теңдеуді пайдалана отырып және энергия En-нің орнына фазалық кеңістікте термодинамикалық шаманың жылдамдығы арқылы үлестіруінің теңдеуін алуға болады. Бұл теңдеуді Максвеллдің үлестіруі дейді.
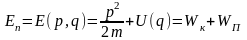 (1)
(1)
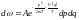 (2)
(2)
(2)-ші теңдеуден кинетикалық және потенциалдық энергияны жеке алатын болсақ,
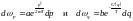 .
.
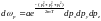 ,
,
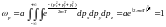
Мұндағы
негізгі мақсат
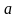 коэффицентін
табу. Ол үшін, мына теңдеуді пайдаланып:
коэффицентін
табу. Ол үшін, мына теңдеуді пайдаланып:
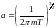
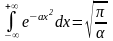 табамыз,
олай болса,
табамыз,
олай болса,
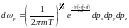 (3)
(3)
(4)-ші теңдеуді Максвеллдің үлестіруі деп атайды. Ал жылдамдыққа байланысты.
 (4)
(4)
 (5)
(5)
Осы
сияқты осцилятордың да үлестіруін
табуға болады:
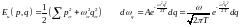 (6)
(6)
Онда
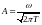 .
.
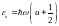 ,
онда
,
онда
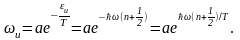
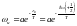 .
.
Таблицалық мәнді пайдалана отырып, а-ны тапсақ, (6)-ші теңдеу осцилятор үшін жазылған теңдеу, бұл да Максвеллдің теңдеуі. Бұл теңдеуді бұрыштық жылдамдық үлестіруінің теңдеуі дейді.
б) Бос энергия үшін. Бос энергияның үлестіру теңдеуі.
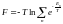 . Дәлелдейік S=ln
(1)
. Дәлелдейік S=ln
(1)
Норма
шарты
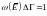 ;
;
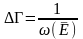 (2)
(2)
 -жалпы
орташа энергия.
-жалпы
орташа энергия.
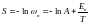 (3)
(3)
өйткені (4)
онда
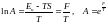 .
(5)
.
(5)
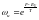 (6)
- бұл бос энергияның үлестіру теңдеуі.
(6)
- бұл бос энергияның үлестіру теңдеуі.
(6) теңдеуді пайдалана отырып, Ғ-ты табуға болады.
 (7), дәлелденді
(7), дәлелденді
себебі
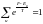 . (8)
. (8)
Сонымен (6), (7), (8)-шы теңдеулер бос энергияның үлестіруінің заңдылығы.
 (9)-(10)
(9)-(10)
(9) мен (6) - ді салыстыратын болсақ,
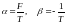 (13)
(13)
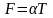 (14),
(14),
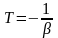 (15),
(15),
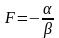 (16)
(16)
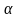 мен
мен
 -ның
қатынасы бос энергияны береді.
-ның
қатынасы бос энергияны береді.
Сонымен біз термодинамикалық шаманың үлестіруінің негізгі теңдеулерін, Гиббстің шамаларының үлестіруінің негізгі теңдеулерін, бұрыштық жылдамдықтар үшін және бос энергия үшін Максвелл үлестіруін таптық. Бұл екі үлестіруді талдау термодинамикалық шамалардың сол термодинамикалық жүйені құрайтын бөлшектер мен күйлердің санына да байланысты екен.
Осыған байланысты біз жеке-жеке бөлшектерден тұратын газдарды қарастырдық. Газдар 2 түрлі болады:
1.Идеал
2.Нақты.
Әдебиеттер: негізгі және қосымша.
