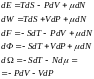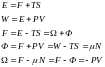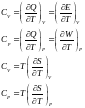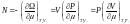- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
Энтропия жалғыз энергия өзгергенде емес көлем өзгергенде де өзгереді. Бұл эксперименттің дәлелдеуі, кейде екеуі де өзгеруі мүмкін. Ал энергия да, көлем де күш әсер еткенде өзгереді.
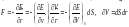 ,
,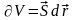 (1)
(1)
Энтропия тұрақты болу үшін энергия тұрақты болу керек. Энергия тұрақты болу үшін көлемді өзгерту керек. Олай болса:
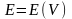 (2)
(2)
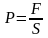 (3) - қысым, яғни күштің бетке әсері.
(3) - қысым, яғни күштің бетке әсері.
(1)-мен (3)-ті салыстырайық
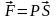 онда
онда
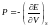 (4)
(4)
(4)-ші теңдеу термодинамикалық қысым деп аталады. Бұдан
 (5)
(5)
Термодинамикалық қысым дегеніміз - энергия өзгеруі мен көлем өзгеруінің арасындағы пропорционалдық. Егер көлем өзгерсе, онда
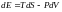 (6)
(6)
(6)-теңдеу термодинамиканың 1-ші бастамасы.
Егер S=const болса, онда (4)
Егер
V=const
болса,
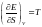
(6)-ші энергияның өзгерісі. Ол S пен V өзгерісіне байланысты.
Жұмыс және жылу мөлшері.
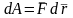 (1) Бұл теңдеу механикадан белгілі.
(1) Бұл теңдеу механикадан белгілі.
Екі нәрсе есте болсын:
Жүйе жұмыс істеу керек
Немесе жүйенің үстінен жұмыс істелуі керек.
Сондықтан мұның жұмыс істеуіне байланысты, бірде оң, бірде теріс бағытта болады.
(2) 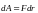 (3)
(3)
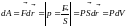 (4)
(4)
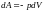
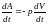 (5)
(5)
немесе 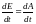 (6)
(6)
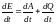 (7)
(7)
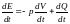 (8)
(8)
 (9)
(9)
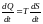 (10)
(10)
Енді жылу сыйымдылығы деген ұғым енгізсек CV, Cp, онда:
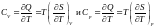
Сv – көлем тұрақты болғанда, ал Cp – қысым тұрақты болғанда.
Онда:
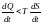 немесе
немесе
 .
.
Жылу функциясы.
Егер
(7)-ні
қарастырсақ
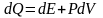 (1)
(1)
Егер де Р-ны тұрақты десек, онда
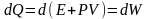 (2)
(2)
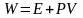 (3)
(3)
W-жылу функциясы, энтальпия.
Егер
Р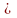 const
const
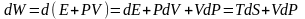
Себебі:
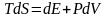 ,
онда
,
онда
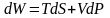 (4)
(4)
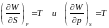 (5)-(6)
(5)-(6)
Еркін энергия.
Изотермалық қайтымды процесс кезіндегі термодинамикалық шаманың өзгерісі төмендегі теңдеумен сипатталады.
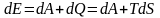
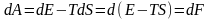 ,
олай
болса
F
= E
-TS
(1)
,
олай
болса
F
= E
-TS
(1)
Не
болмаса
 (2)
(2)
(1)-ші (2)-ші теңдеулерді бос энергия теңдеулері деп атайды. (1)-ші мәнін, ал (2)-ші өзгерісін көрсетеді. (1), (2)-ні талдау арқылы энтропияны, қысымды, бос энергияны (S,P,F) табуға болады.
Егер
T=const болса,
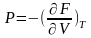 (3)
(3)
Егер
V=const болса,
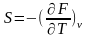 (4)
(4)
E=F+TS E және F байланысы:
E=F-T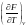 (5)
(5)
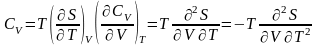
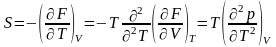
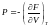 ;
;
 ,
,

1)
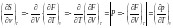
онда
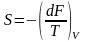 ,
,
2)
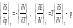 3)
3)
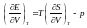 dE=TdS-pdV.
dE=TdS-pdV.
4)
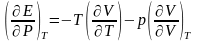
онда табуға болады:
5)
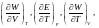
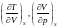 және
және
6)
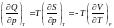 ,
,
және
егер
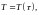 -
температуралық шкала,
-
температуралық шкала,
онда
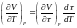 және
және
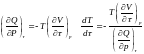 .
.
Әдебиеттер: негізгі және қосымша.
6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
Өткен тақырыптағы (2)-ші теңдікті пайдалана отырып, тағы бір термодинамикалық потенциалды табуға болады. Ол ұшін Р мен V-ның көбейтіндісін дифференцалдаймыз.
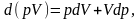
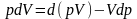
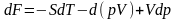 не болмаса
не болмаса
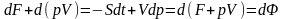
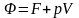 (1)
(1)
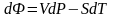 (2)
(2)
(1), (2)- термодинамикалық потенциал немесе Гельмгольцтың энергиясы деп атайды. Бұл тендеуден S,V, -ті таба аламыз.
Егер p=const болса,
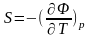 (3)
(3)
Егер T=const болса,
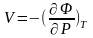 (4)
(4)
енді
(4) (1) қойсақ
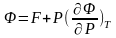 (5)
(5)
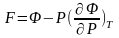 (6)
(6)
Сөйтіп біз 4 атақты термодинамиканың теңдеулерін таптық.
Темодинамиканың негізгі теңдеулері. Бұнда термодинамикалық жүйені құрап тұрған бөлшектер санын ескерсек:
|
|
|
|
|
|
|
|
|
Екінші топта (2) V-ның орнына мәнін қойып, 2 теңдеу алуға болады. Сол сияқты, S-тің орнына да мәнін қойып, 2 теңдеу алуға болады.
Біздің қарастыратынымыз потенциалдың көлем, қысым, энтропия, температураға (P,V,T,S) байланыстылығы ғана. 4 термодинамикалық потенциал немесе 4 энергия тек осы 4-еуіне ғана емес, бұл сол термодинамикалық жүйеге кіретін бөлшектің санына да байланысты екендігі көрсетілген.
5-ші топтағы N-термодинамикалық жүйеге кіретін бөлшектің саны. Енді оны қарастырайық.
Әдебиеттер: негізгі және қосымша.