
- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
Дәріс сабақтардың тезистері
1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
Термодинамикаға тарихи шолу. Термодинамика физиканың бір ерекше бөлімі. Басқа бөлімге қарағанда оның аппаратары ерекше. Оның себебі басқа физикалық денелерге қарағанда ерекше. Оның ерекшелігі, қарастыратың механикалық денелерге кіретің бөлшектердің саны өте көп. Ол бөлшектердің қозғалысын механикалық теңдеулер арқылы сипаттау мүмкін емес. Бұл бөлшектерді сипаттау үшін кванттық тұрғыда қарау да, квантылық теңдеуді де қолдану мүмкін емес. Бұл проблеманы шешу үшін белгілі физикалық ұғымындар мен шамалар жаңа ұғымдар мен шамалар еңгізуге тұра келді. Бұндай шамаларды еңгізу үшін қозғалыс және күй деген, күйдің өзгерісі, күйдін бір жағдайдан екінші жағдайға көшуі және тепе-тендік күй деген принциптерге сүйенуі керек.
Бұл принциптерді еңгізген адамдар Гиббс, Больцман т.б.. Сондықтан ол екеуін термодинамикамен ститикалық физканың негізін салушылар дейді. Бұл кісілер еңгізген ең негізгі ұгымдары.
Ықтималдық -
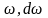
Статискалық үлестіру функциясы -
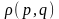 ,
бунда
,
бунда
p - жалпылама импульс, q - жалпылама координат,
Энтропия - S.
Статистикалық үлестіру.
Спектралдық кеңістік – квантылық статистиканың негізі. Термодинамика мен статистикалық физиканы екі тұрғыда қарайды.
Классикалық
Квантық тұрғыда.
Бірақ екеунен де шығатың нәтиже біреу. Классикалық статикада фазалық кеңістік, фазалық геометрия, ал кванттық статистикада спектралдық геометрия пайдаланады. Бұнда спектралдық геометрия мен фазалық геометрия бір-біріне жақын. Айырмашылығы классикалық статикада қозғалыс, құбылыс, өзгеріс үзіліссіз. Ал квантық статистикада дискреттік болып табылады, яғни үзілісті.
Термо дегеніміз – жылу, динамика дегеніміз – күш, кейбір кезде энергия дейді. Сонда термодинамика жылу күші, жылу энергиясы.
Жылуды сипаттайтын ең бірінші шама – температура Т.
Күшті сипаттайтын шама – энергия.
Энтропия.
 -тығыздық.
-тығыздық.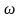 -ықтималдылық.
-ықтималдылық.
Q – жылу мөлшері.
V – көлем.
P – қысым.
W - жылу функциясы, энтальпия.
F - бос энергия
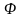 -
Гельмгольц функциясы.
-
Гельмгольц функциясы.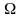 -
Гиббс функциясы. (11)
мен (12)
термодинамикалық потенциал деп
айтылады.
-
Гиббс функциясы. (11)
мен (12)
термодинамикалық потенциал деп
айтылады.Cv , Cp - көлем, қысым турақты болғандағы жылу сиымдылығы.
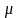 -
химиялық потенциал.
-
химиялық потенциал.N - бөлшек саны.
n - күй саны.
пен (16)-ны классикалық, кванттық екі жағдай арқылы сипаттауға болады.
Термодинамикалық денелерді сипаттау үшін осы екі тұрғыда қарау арқылы қозғалыс, өзгеріс заңдылығын шешуге болады.
Классикалық
тұрғыда қарау үшін фазалық кеңістікте
термодинамикалық денелерді өте кішкентай
фазалық көлемдерге бөледі. Егер dpdq -
жалпы жүйенің көлемі десек,
 немесе
немесе
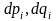 .
i=1,…., n – жүйешіктер саны.
.
i=1,…., n – жүйешіктер саны.
Бұның ерекшелігі бұл кешкентай жүйеге кіретін бөлшектің саны көп, бірақ жалпы жүйеге кіретін бөлщектің санынан көп аз. Осыдан статистика басталады. Мұны Гиббстың ансамблі дейді.
Бұл кешкентай бөлшектерді фазалық нүкте дейді. Оларды берілген бір уақыттағы қозғалысын, өзгерісін фазалық траектория деп атайды. Ал оның қозғалысынан - болған ағынның көлемін фазалық көлем деп атайды.
Классикалық статистика.
Бұл статистиканы екі тұрғыда қарастыруға болады:
Уақыт бойынша және көлем, яғни қозғалыс бойынша.
Уақыт егер шексіз болса онда Т – уақыты дегеніміз термодинамикалық денелердің тепе-тендік күйге келу уақыты. Бұнда біздің қарастыратынымыз тұйық жүйе. Бұл термодинамикалық жүйенің берілген бір моментте бір күйде болу ықтималдылығын мына теңдеумен сипаттауға болады:
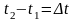 (1) егер
уақыт өзгерісін
(1) егер
уақыт өзгерісін
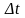 десек онда ықтималдық
десек онда ықтималдық
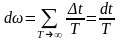 (2)
(2)
(2) уақыт өзгерісі бойынша ықтималдық өзгерісі дейді.
Күйдің өзгерісі бойынша бұл уақытта
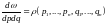 (3)
(3)
егердағы
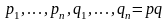 деп алсақ (3) теңдеуді былай жазуға
болады:
деп алсақ (3) теңдеуді былай жазуға
болады:
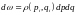 (4)
(4)
(2),
(4) теңдеуілер классикалық статистиканың
негізігі деп аталынады, - ықтималдықтың тығыздығы.
- ықтималдықтың тығыздығы.
(4) теңдеуді интегралдасақ:
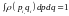 (5) – нормалау шарты.
(5) – нормалау шарты.
(2),
(4), (5) теңдеулер арқылы термодинамикалық
шамалардың орташа мәнін тауып алуға
болады. Егер орташа шаманы
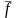 десек, ол:
десек, ол:
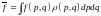 (6)
(6)
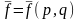 -
орташа шама, ал
-
орташа шама, ал
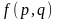 - нақты шама. Егер де
- нақты шама. Егер де
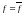 болса, онда ауытқу жоқ.
болса, онда ауытқу жоқ.
Бұны максималдық шарт дейді.
Ал

![]() (7)
болуы да мүмкін:
(7)
болуы да мүмкін:
яғни
ауытқу бар,
 теріс болуыда мүмкін. Сондықтан ауытқу
негізінде оң шама болу керек. Ал ауытқу
оң болу үшін, бұл ауыткуды квадратау
керек, яғни модульдеу керек:
теріс болуыда мүмкін. Сондықтан ауытқу
негізінде оң шама болу керек. Ал ауытқу
оң болу үшін, бұл ауыткуды квадратау
керек, яғни модульдеу керек:
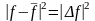 (8)
(8)
Ауытқудың орташа мәндерінің бір қасиеті:
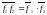
мәндерінің жалпы орташа мәні олардың жеке-жеке орташа мәндерінің көбейтіндісіне тең.
Лиувильдің теоремасы.
Классикалық статистикада процессті үзіліссіз деп қарастырады. Ал кванттылық та дискретті деп қарастырады. Классикалық статистикадағы процесске үзіліссіздік теңдеуін пайдаланады. Ықтималдық үлестірудің тығыздығы
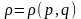 десек,
десек,
осның өзгерісін қарастырайық.
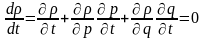 (1)
(1)
стационарлық жағдай үшін
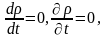
бұны тепе-теңдік тұйқталған күй дейміз.
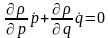 (2)
(2)
Лиувиль теңдеуі. Оны дәлелдейік. Ол үшін үзіліссіздік теңдеуін жазайық:
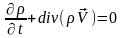 (3)
(3)
термодинамика үшін
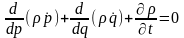 (4)
(4)
 (5)
(5)
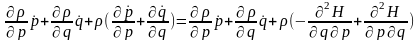
Бұған Гамильтоның каноникалық теңдеуін пайдаландық:
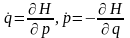 ,
онда (2) теңдеу шығады, дәлелденеді.
,
онда (2) теңдеу шығады, дәлелденеді.
теңдеу нольге тең болу үшін p -ға, q-ға байланысты тұрақты шама болу керек.
 немесе
=0
немесе
=0
егер p мен q-ға тәуелді өзгермесе, немесе -ның өзы нольге тең болса ғана теңдік орындалады. Олай болса фазалық көлем күй өзгергенімен ол өзгермейді, яғни фазалық көлем сақталады. Бұл жүйе тұйықталған және тепе-тендік жағдайда болса өзгермейді. Бұл теорема Лиувильдің теоремасы деп айталады. Бұдан шама:
көлем аддитивті былайша айтқанда
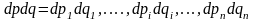
жалпы көлем жүйекшіктердің көлемнің қосындысынан тұрады. Олай болса статистикада.
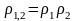 ,
,
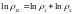
Бұл жүйешелер Гиббстің ансамблін құрайды. Сондықтан Лиувиль теоремасы арқылы соның салдары Гиббстің ұғым еңгіземіз, бұл бүкіл термодинамикалық шаманың жиынтығы ансамбльін кұрайды.
Классикалық механикада, классикалық статистикада не бары 7 қозғалыс интегралы бар, яғни 7 сақталу заңы бар. Бұл 7 аддитивті шама болады. Мысалы, Е=T+U=const кинетикалық энергия артса, потенциалдық энергия кемиді немесе кері. Ал олардың қосындысы тұрақты. Импульсте де осылай.
Энергия сақталу заңы.
Импульс зақталу заңы.
Импульс моментінің сақталу заңы.
Әдебиеттер: негізгі және қосымша.
