17

Федеральное агентство по образованию

ГОУ ВПО Рыбинская государственная авиационная

технологическая академия им. П. А. Соловьева

Кафедра Общей и технической физики

Лаборатория «Статистическая физика и термодинамика»

Утверждено

на заседании методического

семинара кафедры физики

« » _________ 2007 г.

Зав.каф. Пиралишвили Ш.А.

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО СТАТИСТИЧЕСКОЙ ФИЗИКЕ И ТЕРМОДИНАМИКЕ

ЛАБОРАТОРНАЯ РАБОТА №CТ-3

Изучение спектра излучения нагретого вольфрама

Методическое руководство

разработано доц. Суворовой З.В.,

ассистентом Попковой Е.А. Рецензент Шувалов В.В.

Рыбинск, 2007 г.

УКАЗАНИЯ ПО

ТЕХНИКЕ БЕЗОПАСНОСТИ

К работе с прибором допускаются лица, ознакомленные с устройством, принципом работы и прошедшие инструкцию по технике безопасности.

Прибор имеет подключение к электрической сети. Соблюдайте формы электробезопасности и требования инструкции №4 по технике безопасности. Не включайте прибор в сеть, пока не ознакомитесь с его конструкцией и основными требованиями к работе с ним.

Цель работы: исследование распределения по энергиям фотонов (бозе-частиц) в спектре нагретого тела.

1.Краткие теоретические сведения

1.1.Квантовые статистики

В квантовой физике, как и в статистической, закономерно­сти имеют вероятностный, статистический характер. Однако есть и принципиальное отличие: в квантовой физике статисти­ческий (вероятностный) подход лежит в самой природе микро­частиц, в их волновых свойствах.

Согласно квантовой теории все микрочастицы подразделяют на два класса, которым соответствуют различные квантовые статисти­ки:

- частицы с полуцелым спином называются фермионами и подчиняются статистике Ферми-Дирака;

- частицы с целым спином — бозоны подчиняются статистике Бозе-Эйнштейна.

Других возможностей квантовая теория не допускает. Нет частиц, подчиняющихся классической статистике Больцмана. Последняя является приближенным предельным случаем, в ко­торый переходят при определенных условиях эти две кванто­вые статистики. Физическая природа различия этих двух квантовых статистик вытекает из принципа неразличимости тождественных частиц, согласно которому суще­ствуют два типа волновых y -функций, описывающих состояние тождествен­ных частиц, — симметричные и антисимметричные.

Во всех трех статистиках (классической, Бозе -Эйнштейна и Ферми-Дирака) допустимые микросостояния считаются равно­вероятными. Но различие их — в способах определения мик­росостояний и статистических весов. В статистике Больцмана считается, что даже тождественные частицы принципиально различимы. В квантовых же статистиках, наоборот, считается, что тождественные частицы принципиально неразличимы.

В статистике Ферми-Дирака в каждом квантовом состоянии может находиться не более одной частицы (принцип Паули), а в статистике Бозе - Эйнштейна - любое число частиц.

Различие статистик поясняет табл.1.1, где показано как в каждой из них размещаются две тождественные частицы а и b по трем квантовым состояниям (клеткам). Видно, что в статистике Больцмана всех микросостояний де­вять и вероятность каждого из них равна 1/9.В статистиках же Бозе-Эйнштейна и Ферми-Дирака состоя­ния в первых трех парах распределения Больцмана неразличи­мы, и каждая пара рассматривается как одно состояние. Части­цы а и b принципиально неразличимы, поэтому они обозначе­ны просто точками. Для бозонов число

микросостояний равно шести, и вероятность каждого из них 1/6. Для фермионов по­следние три распределения статистики Бозе -Эйнштейна невоз­можны (принцип Паули). Остается только три микросостоя­ния, и вероятность каждого из них равна 1/3.

Основная задача квантовых статистик - это нахождение соответствующих им функций распределения частиц по тем или иным параметрам (например, по энергиям), а также определение средних значений этих параметров, ха­рактеризующих наиболее вероятное макросостояние всей сис­темы частиц.

Таблица 1.1

Для описания состояния системы частиц рассматривают во­ображаемое шестимерное пространство, каждая точка которого характеризуется шестью координатами: х, у, z, р_х, р_y, р_z. Это так называемое фазовое пространство. Состояние системы определяется тем, как распределены в этом пространстве точ­ки, изображающие состояния всех N частиц системы. При этом нужно учесть присущий частицам корпускулярно-волновой ду­ализм, согласно которому неопределенности координаты х и со­ответствующей проекции импульса р_х могут быть определены только с неопределенностью dx и dр_х, произведение которых, согласно принципу неопределенностей Гейзенберга, dxdp_x³ h. Аналогично и для других пар: y и р_у, z и р_z. Поэтому естественно считать, что данному состоянию части­цы в фазовом пространстве соответствует не точка, а фазовая ячейка, объем которой

. (1.1)

Распределение частиц по таким фазовым ячейкам есть пре­дельно подробное квантовое описание состояния системы.

Квантовые распределения представля­ют собой функции , определяющие средние числа частиц в одной фазовой ячейке с энергией , или функции заполнения ячеек:

для фермионов , (1.2)

для бозонов . (1.3)

Здесь m - так называемый химический потенциал (некоторая характерная энергия, значение которой можно найти из усло­вия нормировки: суммарное число частиц во всех фазовых ячейках должно быть равно полному числу N частиц макроси­стемы).

Остановимся подробнее на особенностях этих распределе­ний.

1. Для фермионов функция не может быть больше еди­ницы, а для бозонов ее значение может быть любым ( ³0).

2. Если <<1, то в знаменателях обоих распределений можно пренебречь единицей, и формула переходит в

, (1.4)

т.е. в распределение Больцмана (А — нормировочный коэффи­циент). Значит, классическое распределение Больцмана спра­ведливо лишь тогда, когда малы «числа заполнения» фазовых ячеек,— при условии <> << 1. В этом случае речь идет о совпадении формул, а отнюдь не о том, что изменя­ется поведение частиц (фермионы остаются фермионами, бозо­ны — бозонами).

3. В макросистеме уровни энергии частиц квазинепрерыв­ны (расположены очень плотно). Поэтому индекс i у можно опустить.

4. Для бозонов значения m в (1.3) не могут быть положитель­ными, иначе при 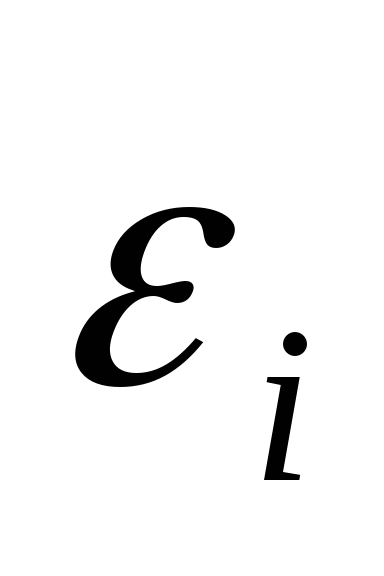< m окажется, что < 0, а это лишено физи­ческого смысла. Таким образом, для бозонов m < 0. У макроси­стем с переменным числом бозонов (к числу которых относят­ся, например, фотоны) m = 0, и формула (3) переходит в

. (1.5)

Для фермионов подобного ограничения не существует.

До сих пор мы имели дело с функ­цией , характеризующей среднее число частиц с энергией e в одной фазовой ячейке. Для дальнейших целей не­обходимо найти число фазовых ячеек, в интервале энергий .

Чтобы определить , найдем сначала соответствующий объем dL фазового шестимерного пространства. Для этого в им­пульсной части фазового пространства выделим шаровой слой радиусом, равным импульсу p частицы, и толщиной . Его объем равен . Умножив его на объем координатной части фазового пространства (это объем макросистемы), получим искомый элемент объема фазового пространства:

. (1.6)

Число фазовых ячеек в этом элементе объема получим, разделив на объем одной фазовой ячейки, равный соглас­но (1.1). Кроме того, в дальнейшем нас будет интересовать чис­ло фазовых ячеек, приходящихся на единицу объема обычного пространства, поэтому будем считать, что = 1. Таким обра­зом, число фазовых ячеек в расчете на единицу объема, занима­емого газом, будет равно

. (1.7)

Эта величина имеет размерность м

Переход от импульсов к энергиям зависит от природы час­тиц. Это будет конкретизировано в дальнейшем.

Зная число фазовых ячеек в ин­тервале энергий и среднее число частиц в каждой ячейке, т.е. функцию заполнения f, мы можем найти число ча­стиц dn в данном интервале энергий (в расчете на единицу объ­ема газа):

(1.8)

где g — числовой коэффициент порядка единицы, связаный со спецификой частиц идеального газа.