4.1 Средняя квадратичная ошибка, кривая гаусса, доверительный интервал

Выше нами указано, что среднее арифметическое значение измеряемой величины равно

Средняя абсолютная погрешность

,

где n – число измерений.

Часто, обрабатывая результаты, находят среднее квадратичное отклонение от среднего значения

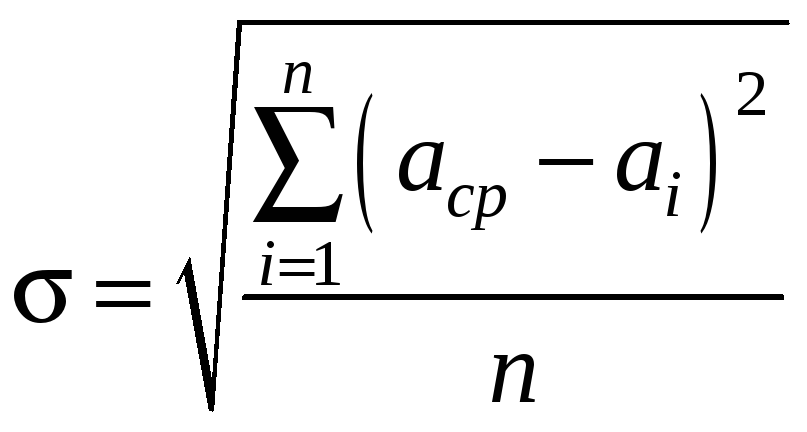
По закону Гаусса функция распределения случайных величин (в нашем случае значений ) записывается

и имеет вид

Точки соответствуют точкам перегиба на кривой Гаусса.

Задача обработки серии измерений сводится к нахождению параметров кривой и .

Зная функцию распределения случайных величин можно вычислить вероятности, с которыми истинное значение будет находиться в том или ином интервале значений. Этот интервал называется доверительным. Например,

<<

Это значит, что истинное значение непосредственно измеренной величины с вероятностью около 0,7 находится в указанном интервале. С расширением интервала вероятность возрастает. При интервале Р=0,955.

Исходя из сказанного найденное значение величины , можно представить

(с вероятностью 0,683)

(с вероятностью 0,955).

5. Приборы для измерения линейных размеров и правила пользования

Для измерения линейных размеров тел используют мерные плиты, линейки, штангенциркули, катетометры, длинномеры, микромеры и т.д.

Рассмотрим устройство штангенциркуля и микрометра.

Штангенциркуль состоит из штанги с губкой. На штанге нанесена миллиметровая линейка (масштаб). По штанге движется рамка с другой губкой. На рамке находится дополнительная линейка – нониус. Нониус изготавливается так, что число его делений на одно меньше, чем совпадающее с ним число делений масштаба. Например, , где К – цена деления нониуса.

наименьшая величина, измеряемая штангенциркулем.

Если губки штангенциркуля сжаты, то нуль нониуса и нуль масштаба совпадают. Если совместить штрих первого деления нониуса со штрихом первого деления масштаба, то между губками и будет расстояние 0,1 мм. Если совместить штрих второго деления нониуса со вторым штрихом линейки, то между губками будет 0,2 мм и т.д. При совмещении десятого деления нониуса с десятым деление линейки между губками расстояние будет 1 мм. Фактически, указанными действиями мы измеряли расстояние (размеры) 0,1 мм, 0,2 мм, 0,3 мм и т.д.

Если у штангенциркуля 10 делений нониуса совпадают с 19 делениями линейки, то , т.е. цена деления нониуса другая, а наименьшая величина, измеряемая штангенциркулем .

В этом случае расстояние между губками будет 0,1 мм при условии, что штрих первого деления нониуса совпадает со штрихом второго деления линейки.

При измерении реального объекта его размеры определяют так: отсчитывают целое число миллиметров по линейке до нуля нониуса, затем смотрят, которое деление нониуса точно совпадает с делением линейки. Номер этого деления и показывает число десятых долей. За погрешность штангенциркуля принимается наименьшая измеряемая им величина.

Микрометр состоит из полого стержня со шкалой, соединенного со скобой. В полом стержне помещается микровинт с прикрепленным к нему барабаном. Измеряемый предмет помещают между стержнем скобы и торцем микрометрического винта. По горизонтальной шкале на стержне ведут отсчет в миллиметрах, а самые доли отсчитывают по круговой шкале барабана.