ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Московский государственный университет

приборостроения и информатики

кафедра высшей математики

Выборнов А.Н.

ОБРАЗЕЦ ТЕСТА

ПО ТЕОРИИ ВЕРОЯТНОСТИ

С РЕШЕНИЕМ

Москва 2015

Вопрос №1:

В урне 9 шаров, из которых 5 белых и 4 черных. Из урны вынимают 4 шара. Найти вероятность того, что среди них будет 2 белых и 2 черных.

Решение

Используем общую формулу для задачи:

В урне шаров, из которых и белых. Из урны вынимают шаров. Тогда вероятность того, что среди них будет белых и черных, определяется формулой:

В рассматриваемом вопросе , , , . Поэтому

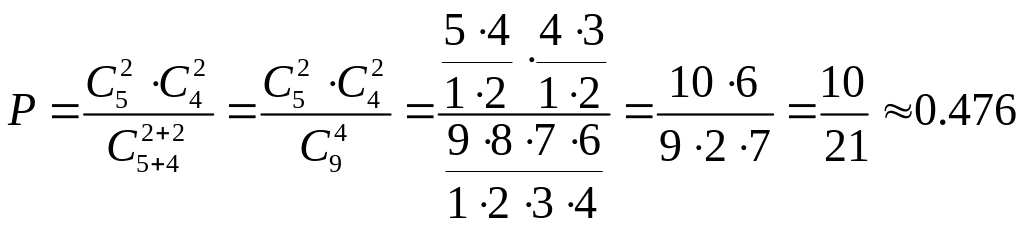
Замечание: Число сочетаний вычисляется по формуле: , где знаком «n!» обозначается факториал числа, равный произведению всех натуральных чисел от 1 до n. Например, 4!=

Принято, что 0!=1!=1.

Замечание 2: число сочетаний - всегда равно натуральному числу, не может быть дробным или отрицательным.

Замечание 3: вероятность любого события всегда находится в пределах от 0 до 1, что справедливо для любого вопроса из теста, где требуется найти вероятность. Если в ответе получается отрицательное число, или число большее единицы, следует проверить решение на арифметические ошибки!

Вопрос №2:

Плотность распределения случайной величины X задана формулой

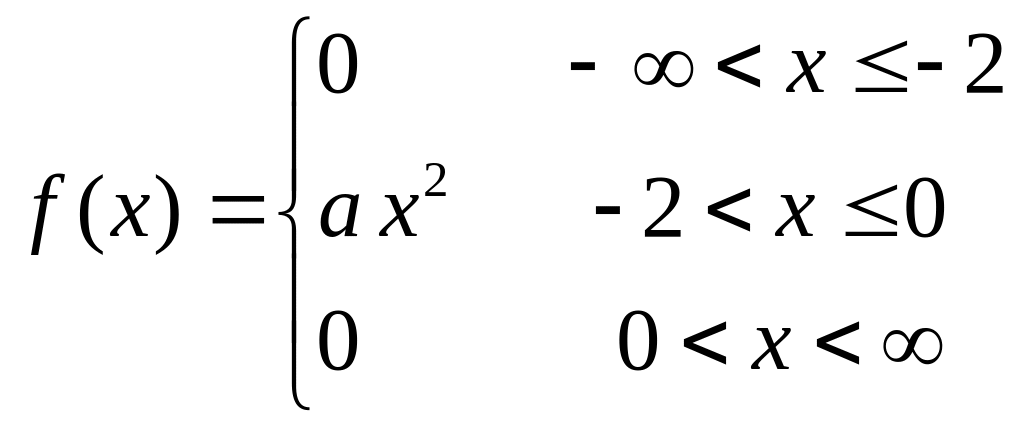
Вычислить математическое ожидание этой случайной величины.

Решение

Сначала необходимо найти константу из условия .

Итак:

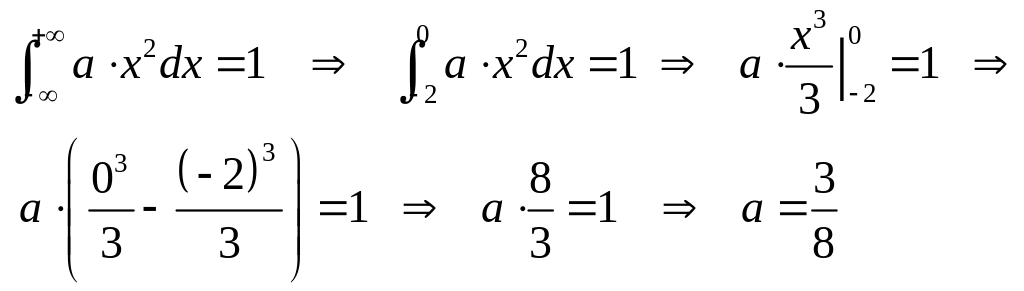
Интеграл вычислялся в пределах от (-2) до 0 , так как только на этом промежутке функция отлична от нуля.

Теперь мы имеем полное выражение для плотности вероятности случай ной величины Х:

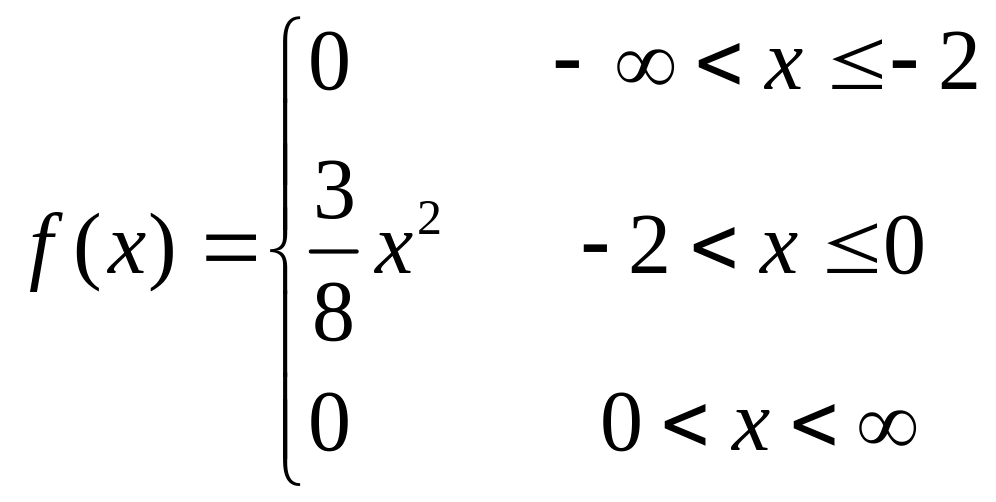
Математическое ожидание непрерывной случайной величины определяется формулой: . Вычисляем:

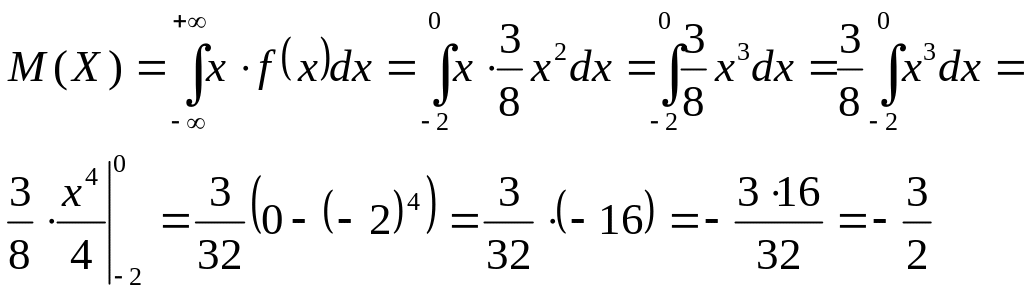
Замечание: математическое ожидание случайной величины является по определению ее средним вероятностным значением. Таким образом, для оценки правильности ответа обратим внимание, что вся случайная величина по условию отлична от ноля только на промежутке от (–2) до 0, следовательно ее среднее значение обязательно должно попасть в этот промежуток.

Вопрос №3:

Плотность распределения случайной величины X задана формулой

_{Вычислить вероятность попадания случайной величины X в интервал (-1; 9).}

Решение

Как и в предыдущей задаче, сначала необходимо найти константу из условия . Так как плотность вероятности постоянна на отрезке , рассматриваемая случайная величина распределена по равномерному закону на отрезке , и константа будет равна .

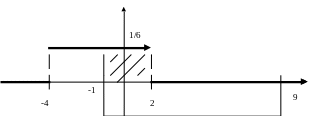
На рисунке изображен жирными линиями график плотности вероятности величины Х. Вероятность попадания этой величины на интервал (-1; 9) равна площади, заключенной между графиком и осью абсцисс на этом интервале. На картинке – это площадь заштрихованного прямоугольника. Ширина этого прямоугольника равна 2-(-1)=3, а высота, как мы установили вначале, равна . Поэтому его площадь равна