Задача про багатополюсний найкоротший ланцюг. Алгоритм Флойда

Алгоритм Дійкстри не дозволяє розв’язувати задачі з від’ємними довжинами дуг. Для розв’язування таких задач використовується алгоритм Флойда, який знаходить найкоротші ланцюги між всіма парами вузлів мережі. Неорієнтована дуга заміняється парою орієнтованих в протилежних напрямках дуг з такими ж довжинами, як у неорієнтованої. Довжини дуг можуть бути від’ємними, однак довжина кожного циклу повинна бути невід’ємною. Нехай — множина вузлів мережі, — довжина орієнтованої дуги , — довжина найкоротшого ланцюга з вузла в вузол , — матриця віддалей, — матриця маршрутів.

Алґоритм Флойда будується, виходячи з наступних міркувань. Нехай — найкраща біжуча оцінка довжини найкоротшого ланцюга з вузла i в вузол k. Розглянемо довжину найкоротшого ланцюга з i в k, який проходить через певний проміжний вузол j — . Якщо , то біжуче значення . Виходячи з цього алгоритм Флойда працює наступним чином:

• початкова оцінка довжини найкоротшого шляху становить значення , і далі послідовно перевіряються всі проміжні вузли, що розташовані між і та k;

• якщо довжина ланцюга, що проходить через деякий проміжний вузол менша, ніж біжуче значення оцінки, то це значення присвоюється оцінці.

Ця процедура повторюється для всіх пар вузлів до того часу, поки не будуть отримані значення найкоротших віддалей.

Алгоритм Флойда (версія, вдосконалена Ху).

Крок 1. Початкові присвоювання значень елементам матриць віддалей та маршрутів — для всіх , :

; ; ; (параметр використовується для позначення базового вузла на кожній ітерації).

Крок 2. . Якщо , то стоп: значення найкоротших віддалей між всіма парами вершин знайдені та зберігаються в матриці , а маршрути — в матриці . В іншому випадку вузол буде базовим. Викреслюємо базовий стовпчик та базовий рядок матриці , а також ті її рядки та стовпчики, які мають значення , що знаходиться в базовому рядку та стовпчику.

Крок 3. Перерахунок значень елементів матриць та . Для всіх , , :

.

Розрахунки на цьому кроці доцільно виконувати з врахуванням викреслених рядків та стовпчиків. Викреслювання є мнемонічним прийомом, що полегшує розрахунки за вищенаведеними формулами, а також виключає непотрібні перерахунки значень.

Порівнюємо кожен невикреслений елемент з сумою елементів згідно до вищенаведеного та переписуємо перераховані значення в матриці наступної ітерації. Викреслені елементи переписуємо без змін.

Перехід до кроку 2.

Приклад. Знайти найкоротші віддалі між всіма парами вершин мережі:

Початкові присвоювання:

Подальші обчислення виконуємо згідно до алгоритму:

1-а ітерація. Вузол є базовим. В матриці викреслюється перший рядок та перший стовбець. Стовпці 3,5,6,7,8 мають в базовому рядку безмежність, а рядки 3,5,6,7,8 — безмежність в базовому стовпчику, і таким чином теж викреслюються. Таким чином перерахунок слід здійснити лише для наступних елементів матриці — d₂₂, d₂₄, d₄₂, d₄₄ :

Так як діаґональні елементи матриці не перераховуються, перераховуємо значення тих, що залишилися:

.

Таким чином в матриці перерахованими порівняно з матрицею будуть елементи, що розглядалися вище, а інші перейдуть без зміни з . Відповідно зміняться лише 2 елементи матриці . Таким чином:

2-а ітерація. Вузол буде базовим. Викреслюємо в матриці другий рядок та другий стовпчик, а також 6-8-й стовпчик та 6-8-й рядок як такі, відповідні елементи яких в базовому рядку та базовому стовпчику рівні безмежності, і діаґональні елементи, отримуючи множину елементів матриці , значення яких повинні бути перераховані:

В результаті перерахунку отримаємо:

Інші з елементів в результаті перерахунку збережуть попередні значення, а тому не зміняться й відповідні значення .

Таким чином , і матриці будуть мати вигляд:

Результати обчислень, отримані на наступних ітераціях, наведені нижче.

,

,

.

На наступних ітераціях матриці , , залишаються незмінними.

Розглянемо найкоротший шлях з вузла 1 до вузла 5 :

• довжина цього шляху становить ;

• за допомогою матриці 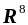визначаємо проміжні вузли — ; таким чином це шлях .