8. Составить структурно-алгоритмическую схему системы автоматического управления.

Исходная схема автоматического управления имеет вид:

Выполним преобразования схемы, чтобы найти эквивалентные передаточные функции относительно сигнала основного источника и сигнала уставки.

Перенос сумматора:

Объединение звеньев:

Эквивалентная передаточная функция относительно E₀:

Эквивалентная передаточная функция относительно х_уст:

9. Построить область устойчивости системы в плоскости коэффициентов К_р и К_д, где К_р – коэффициент передачи звена, эквивалентирующего регулятор, а К_д – коэффициент передачи звена, эквивалентирующего датчик текущего значения регулируемой переменной.

Эквивалентная передаточная функция:

Подставим значения известных параметров:

Характеристический полином:

Границы устойчивости определим из причин нарушения устойчивости:

1) Появление нулевого вещественного корня:

2) Появление бесконечного корня:

3) Равенство нулю предпоследнего минора матрицы Гурвица:

Матрица Гурвица:

Предпоследний минор:

Получим, что границы устойчивости определятся следующими уравнениями:

1)

2)

Построим границы устойчивости:

Имеем 5 областей. По критерию Гурвица проверим области на устойчивость. Определитель матрицы Гурвица и все ее диагональные миноры должны быть положительны.

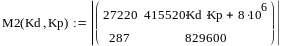
1 область:

2 область:

3 область:

4 область:

5 область:

Следовательно, областью устойчивости является область 5

10. Подготовить имитационную модель системы автоматического управления. Выполнить моделирование процесса включения системы питания при нулевых начальных условиях для заданных преподавателем величин коэффициентов К_р и К_д.

Структурно-алгоритмическая схема САУ имеет вид:

Модель в программном комплексе РИТМ будет иметь следующий вид:

BLT103 – генератор кусочно-постоянного сигнала ( и )

BLT135 – сумматор

BLT133 – инерционное звено I-ого порядка (регулятор, исполнительный механизм, нагрузка)

BLT089 – пропорциональное звено (датчик)

BLT014 – осциллограф

BLT015 – табулятор

Выполним моделирование процесса включения при нулевых начальных условиях.

К_р=2 К_д=4

Из осциллограммы в п.10 видно, что в установившемся режиме величина ЭДС регулируемого источника не равна нулю и сигнал с выхода нагрузки не выходит на уставку.

11. Выбрать значения коэффициентов К_р и К_д из области устойчивости в статическом режиме обеспечивают нулевую величину э.д.с. Е_р регулируемого источника. По результатам эксперимента рассчитать статизм, перерегулирование и длительность переходного процесса для выбранных значений коэффициентов К_р и К_д. Рассчитать теоретические значения указанных показателей.

Как было видно из п. 10 сигнал ЭДС регулируемого источника не выходит на уставку. В установившемся режиме (p=0) E_р определяется следующим образом:

Из выражения видно, что для того чтобы в установившемся режиме E_р=0 необходимо, чтобы x₂₀₁=0, т.е. сигнал с выхода сумматора:

В установившемся режиме х=100, поэтому необходимо изменить К_д:

Проведем моделирование процесса включения при К_р=2 К_д=1

Из осциллограммы видно, в установившемся режиме E_р=0 и х=100

Для разделения схемы на сильноточную и слаботочную необходимо задать К_д=0,1.

Произведем моделирование процесса при К_д=0,1 и К_р=2

В установившемся режиме Е_р не равен 0 и сигнал с выхода нагрузки не равен 100. Необходимо обеспечить:

Но при таких данных это не выполняется, т.к.:

Поэтому введем в схему пропорциональное звено с передаточной функцией:

Подберем значение коэффициента К_пр:

Модель в программе РИТМ:

BLT103 – генератор кусочно-постоянного сигнала

BLT135 – сумматор

BLT133 – инерционное звено I-ого порядка

BLT089 – пропорциональное звено

BLT014 – осциллограф

BLT015 – табулятор

Выполним моделирование процесса включения:

Теперь в установившемся режиме E_p=0 и х=100.

Для расчета статизма необходимо воздействие выполним моделирование при ЭДС основного источника равном 300.

Рассчитаем статизм перерегулирование и длительность переходного процесса.

Статизм:

Перерегулирование:

Длительность переходного процесса:

Рассчитаем эти же параметры теоретически

Передаточная функция:

Характеристический полином:

Корни характеристического полинома:

λ₁=-47.885282

λ₂=-23.478962+9.525612i

λ₃=-23.478962-9.525612i

Показатель колебательности:

Перерегулирование:

Статизм:

Передаточная функция имеет следующий вид:

В установившемся режиме р=0 и статизм определится следующим образом:

Длительность переходного процесса:

Сравним теоретические и экспериментальные результаты:

Определение	, %	, %	T, c
Теоретическое	0,786	23,321	0,127
Экспериментальное	0,043	23,32	0,100
Погрешность, %	94,5	0,004	21,3

Расчет погрешности: