Тема 5 Индексный метод в статистических исследованиях Индексный метод в статистике

5.1. Содержание задания и требования к нему.

По теме 5 «Индексный метод в статистике» для каждого студента номер задачи, приведенной в приложении 5, соответствует последней цифре номера зачетной книжки.

Расчеты по задаче должны быть выполнены с приведением формул в развернутом виде и сопровождаться пояснениями и выводами по результатам.

5.2. Методические указания к выполнению задания по теме 5

В статистике индексами называются относительные показатели, выражающие изменения сложных экономических явлений, состоящих из непосредственно несоизмеримых элементов.

Различают индивидуальные и сводные (общие) индексы. Индивидуаль-ные индексы ( i ) дают сравнительную характеристику изменения отдельных элементов той или иной совокупности (состоящей из непосредственно несоизмеримых элементов).

Индивидуальный индекс обозначают буквой с подстрочным указанием индексируемого показателя. Индексируемым называют показатель, изменение которого характеризует индекс. Так, например, для характеристики выполнения планового задания по производству отдельных видов продукции рассчитывают индивидуальные индексы физического объема продукции по формуле:

где:  – объем производства какого-либо вида продукции в натуральном выражении соответственно в отчетном и базисном периодах, который является индексируемой величиной.

Сводный (общий) индекс характеризует изменение явления, состоящего из разнородных непосредственно не суммируемых элементов. Для того, чтобы рассчитать сводный индекс, необходимо прежде всего преодолеть несуммарность (несопоставимость) отдельных элементов изучаемого явления. Это достигается путем введения дополнительного показателя, который позволяет разноименные продукты свести к единству, сделать их соизмеримыми.

Так, для продукции народного хозяйства, как совокупности разноименных вдов изделий, несмотря на их различные потребительские свойства, общим является то, что все они представляют собой результат труда, затраты которого могут быть выражены как в единицах рабочего времени (человеко-часах), так и в стоимостной форме. Эти показатели – время, стоимость – могут быть использованы как соизмерители и называются весами индекса. Умножив индексируемый показатель на соответствующий вес, мы тем самым выражаем элементы анализируемой совокупности в одних единицах измерения, т.е. приводим их в соизмеримый вид, поэтому их уже можно суммировать и сопоставлять. Так, например, умножив объем различных видов изделий на их себестоимость, мы выражаем их в стоимостной форме, что позволяет их суммировать и сопоставлять. При этом, чтобы индекс отражал изменение только индексируемой величины, веса индексов берут на одном уровне. Если в качестве веса используются объемные показатели (продукция, численность), их берут на уровне текущего (отчетного) периода, если качественные показатели (цена, себестоимость, затраты времени на единицу продукции), то их принимают на уровне базисного периода.

В расчетах широко используются индексы физического объема продукции, индекс себестоимости, индекс затрат, индекс цен, индекс товарооборота (стоимости товарооборота), индекс производительности и др.

Сводный индекс физического объема продукции (реализованной продукции) определяют по формуле:

где:  – объем продукции каждого вида изделий соответственно отчетного и базисного периодов (индексируемый показатель);

– цена отдельных видов продукции в базисном периоде (вес индекса).

Сводный индекс цен определяют по формуле:

где:  – цена отдельных видов продукции соответственно в отчетном и базисном периодах (индексируемый показатель);

– объем реализованной продукции в отчетном периоде (вес индекса). Он характеризует, как изменились цены в среднем на различные виды продукции в анализируемой совокупности.

Сводный индекс товарооборота определяют по формуле:

где:  – размер товарооборота соответствующего периода. Он харак-теризует изменение товарооборота продукции различных видов в динамике.

Сводный индекс себестоимости определяют по формуле:

где:  – собственность отдельных видов продукции в текущем и базисном периодах.

Он характеризует как в среднем изменяется себестоимость продукции различных видов в целом по анализируемой совокупности.

Сводный индекс физического объема, взвешенного по себестоимости, определяют по формуле:

Сводный индекс затрат определяют по формуле:

где:  – затраты по производству различных видов продукции соответствующего периода.

Он характеризует, как изменились затраты по производству продукции различных видов в целом по анализируемой совокупности.

Сводный индекс производительности труда определяют по формуле:

где:  – затраты времени на производство единицы продукции в единицу времени соответственно в текущем и базисном периодах.

Он характеризует изменение производительности труда в среднем по различным видам работ.

Индекс производительности труда является показателем, обратным индексу трудоёмкости, который определяется по формуле:

Он характеризует, как в среднем изменились затраты времени на единицу продукции в связи с ростом производительности труда.

Сводный индекс массы отработанного времени определяют по формуле:

где:  – время, затраченное на производство всей продукции соответственно в отчетном и базисном периодах.

Расчет индексов может быть выполнен в агрегатной форме и в форме средних индексов – среднеарифметического взвешенного и среднегармони-ческого. Все вышеприведенные индексы рассчитаны как агрегатные индексы. Выбор формы расчета индексов зависит от наличия исходных данных. Если известны значения индексируемого показателя и веса в отчетном и базисном периодах, то пользуются агрегатной формой индексов. Если отсутствуют значения индексируемого показателя или веса в текущем и базисном периодах, но известны изменения индексируемого показателя или веса по отдельным единицам анализируемой совокупности, пользуются формой средних индексов. Например, известны размер товарооборота в базисном периоде и изменение физического объема отдельных видов продукции . Необходимо определить индекс физического объема продук-ции . Индекс физического объема продукции определяют по формуле:

Для решения задачи неизвестен выпуск продукции в отчетном периоде, но задан рост каждого вида продукции , который определяют по формуле:

Отсюда

Подставляя найденную величину в исходную формулу, имеем:

Это средняя арифметическая взвешенная индекса физического объема. Соответственно индекс называют среднеарифметическим индексом.

Или, например, известны размер товарооборота в отчетном периоде , а также изменение цен в отчетном периоде по сравнению с базисным по отдельным видам изделий . Необходимо определить, как в среднем изменились цены по всем видам изделий, т.е. индекс цен .

Индекс цен определяют по формуле:

В нашем примере известен товарооборот в отчетном периоде , а товарооборота в ценах базисного периода нет, но заданы индивидуальные индексы цен по каждому виду изделий , которые определяют по формуле:

Отсюда можно определить цены базисного периода:

Подставляем их в исходную формулу:

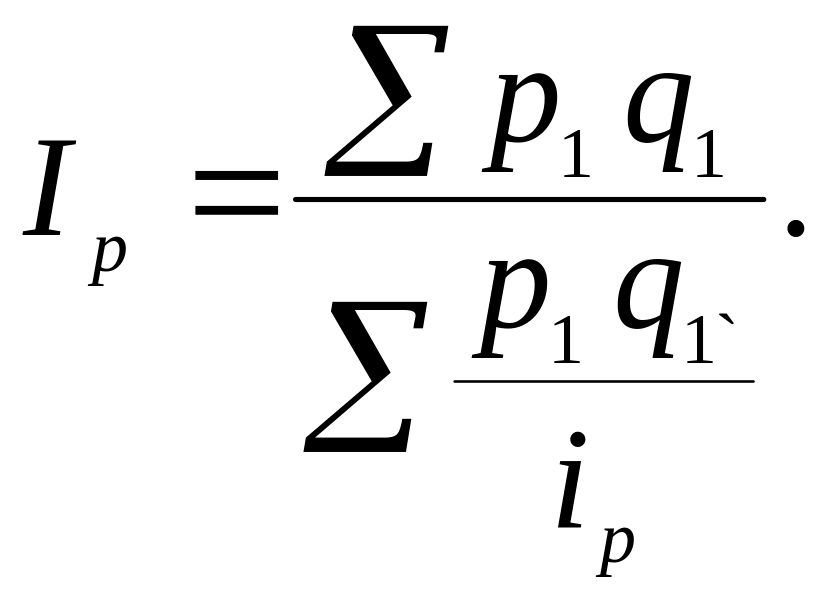
Это средняя гармоническая индекса цен. Соответственно его называют среднегармоническим индексом.

Индексы подчиняются той же взаимосвязи, что и характеризуемые ими показатели. Так, например, товарооборот определяется как произведение цены единицы продукции на объем продукции. Соответственно, и индекс товарооборота равен произведению индекса цен на индекс физического объема продукции:

Пользуясь взаимосвязью индексов можно по величине двух из них определить величину третьего.

На изменение среднего значения показателя Х оказывает влияние как изменение значений осредняемого признака Х, так и изменение весов f. Если в числителе и знаменителе сводного индекса веса берутся (фиксируются) на уровне одного и того же периода, то он называется индексом фиксированного состава и определяется по формуле:

Индекс переменного состава представляет соотношение средних уровней изучаемого явления. Если индекс постоянного (фиксированного) состава показывает среднее изменение лишь одной индексируемой величины, то индекс переменного состава характеризует общее изменение средней как в результате изменения индивидуальных значений индексируемой величины, как и в результате изменения структуры совокупности (весов). Индекс переменного состава определяют по формуле:

Для отражения влияния изменений в структуре изучаемой совокупности на динамику изучаемого явления вычисляется индекс структуры (структурных сдвигов) по формуле:

Взаимосвязь между индексами:

При изучении товарооборота используют:

- индекс цен фиксированного состава:

- индекс переменного состава:

-индекс структурных сдвигов: