2.6.Схематическое изображение идей 1-го и 2-го рангов

Рис.2.1. Уменьшение высоты прыжка

1. Вышка с нормальной высотой прыжка;

2. Спортсмен;

3. Бассейн

4. Спортсмен в полете;

5. Вышка с уменьшенной высотой прыжка.

Рис.2.2. Уменьшение площади контакта с поверхностью воды

1. Вышка;

2. Спортсмен;

3. Бассейн;

4. Спортсмен с большой площадью контакта о поверхность воды;

5. Спортсмен с уменьшенной площадью контакта о поверхность воды.

2.7. Ранжирование идей по итогам работы экспертной группы. Оценка достоверности результатов экспертной группы

Применяется среднеарифметический метод обобщения итоговых результатов 4-х экспертов с указанием их фамилий. Рассчитываются среднеарифметическая значимость и ранг каждой идеи.

Достоверность ранжирования идей различными экспертами проверяется по:

относительному размаху значимостей;

размаху суммарных рангов;

дисперсии суммарных рангов

Таблица 4. Итоги работы экспертной группы. Ранги

№	функция	Ранг				∑рангов Ri	итоговый ранг	разность (Ri-Rср)	кв. разностей
		Туркин	Королева	Петров	Оспельников
34	вертикальный вход в воду	6	1	1	3	11,0	1,0	-9.8	9.6
19	улучшить технику прыжка	7	5	5	4	21,0	4,0	0.2	0.04
20	упростить прыжок	4	4	4	10	22,0	6,0	1.2	1.44
4	уменьшить высоту вышки	8	2	10	2	22,0	6,0	1.2	1.44
13	снизить скорость прыжка	2	4	9	9	24,0	8,0	3.2	10.24
9	дополнительная защита	5	9	8	5	27,0	10,0	6.2	38.44
7	уменьшить вес	3	3	7	6	39,0	3,0	18,0	3.24
11	уменьшить площадь контакта с поверхностью	6	7	3	8	24,0	8,0	3.2	10.24
10	прыгать в бурлящую воду	8	6	2	1	17,0	2,0	-3.8	14.44
26	уменьшить силу натяжения воды	1	8	6	6	21,0	4,0	0.2	0.04
						208		0
					Rср=	20,80

Оценка достоверности по размаху суммарных рангов

Суммарный ранг – это сумма рангов, выставленных всеми экспертами по конкретной i-й идее.

Размах суммарных рангов характеризует разность между максимальным и минимальным значениями суммарных рангов, полученных по всем идеям.

Размах определяется по формуле

где R_max, R_min – максимальное и минимальное значение суммарных рангов, выставленное экспертами по всем идеям.

Достоверность определяется исходя из условия

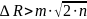
где m – количество идей; n – число экспертов группы

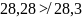
Условие достоверности не выполняется.

Оценка достоверности по дисперсии суммарных рангов

Дисперсия суммарных рангов характеризует отношение суммы квадратов разностей между суммарным рангом i-й идеи и среднеарифметическим значением суммарных рангов по всем идеям к количеству идей за минусом единицы.

Дисперсия рассчитывается по формуле

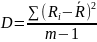
где 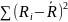– сумма квадратов разностей между суммарным рангом i-й идеи и среднеарифметическим значением суммарных рангов по всем идеям; m – количество идей

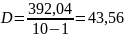
Достоверность определяется исходя из условия

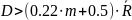
где m – количество идей; – среднеарифметическое значение суммарных рангов

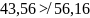
Условие достоверности не выполняется.

Таблица 5. Итоги работы экспертной группы. Значимость

№	функция					βср		макс. размах β		относительный размах β		βijmax-βср		βijmin-βср		B		количество экспертов nэ
		Туркин	Королёва	Дядюшко	Оспельников
34	вертикальный вход в воду	0,08	0,14	0,12	0,15		0,12		0,07		0,21		0,03		0,04		0,04		5,90
19	улучшить технику прыжка	0,06	0,11	0,16	0,13		0,11		0,05		0,39		0,05		0,05		0,05		4,70
20	упростить прыжок	0,12	0,07	0,13	0,02		0,08		0,05		0,54		0,05		0,07		0,07		1,97
4	уменьшить высоту вышки	0,02	0,14	0,11	0,17		0,11		0,06		0,53		0,06		0,09		0,09		1,65
13	снизить скорость прыжка	0,18	0,12	0,07	0,04		0,10		0,08		0,77		0,08		0,06		0,08		2,08
9	дополнительная защита	0,1	0,07	0,1	0,11		0,10		0,02		0,17		0,02		0,03		0,03		6,61
7	уменьшить вес	0,14	0,12	0,06	0,07		0,10		0,04		0,42		0,04		0,04		0,04		5,21
11	уменьшить площадь контакта с поверхностью	0,08	0,08	0,08	0,06		0,07		0,01		0,08		0,01		0,02		0,02		6,77
10	прыгать в бурлящую воду	0,02	0,09	0,13	0,19		0,11		0,08		0,74		0,08		0,09		0,09		1,69
26	уменьшить силу натяжения воды	0,2	0,07	0,08	0,07		0,11		0,09		0,89		0,09		0,04		0,09		1,02

Оценка достоверности по относительному размаху значимостей

Относительный размах значимости (∆βi) ­­­­– характеризует отношение разности между максимальной и минимальной величинами значимости конкретной i-й идеи к ее среднеарифметической величине.

Расчетная численность экспертной группы определяется по формуле

где c – допустимая мера влияния одного из экспертов на групповую оценку; – среднеарифметическая оценка значимости по i-тому методу, полученному от n участников в экспертизе; B – возможная оценка дополнительного эксперта

Из условия влияния суждений одного эксперта на отклонение групповой оценки в пределах от 5 – 10 % принимают

При

При

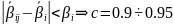
где – значимость i-того метода по данным эксперта

В качестве параметра B применяют максимальное абсолютное значение разности значимости.

Для удобства результаты расчетов приведены в таблице 5.

Проанализировав результаты расчетов приходим к выводу, что количество членов экспертной группы подобрано не верно. Требуется изменение экспертной группы.