1. Работа двигателя на квазистационарном режиме.

Для основного участка работы двигателя ранее было получено соотношение

, которое при постоянстве скорости горения и плотности топлива по поверхности примет вид

Рассмотрим стационарный режим работы двигателя, что как правило соответствует существенному по времени промежутку на диаграмме давления. Тогда . Будем считать, что закон скорости горения описывается степенной зависимостью u= . Тогда

Из последней формулы получается выражение для давления на стационарном режиме . Последнее выражение известно как формула Бори.

Выражение называют параметром заряжания.

Уравнение Бори в частности не учитывает потери рабочего тела на заполнение вновь образующегося при горении топлива внутрикамерного объема.

Если двигатель эксплуатируется при значительном разбросе температур, то это должно быть учтено в законе скорости горения u= /

Этот член нужно подставить в параметр заряжания.

Представленный уровень давления достигается за некоторое время выхода двигателя на режим. Для определения этого времени обратимся к исходному дифференциальному уравнению и будем считать, что горение заряда по всей поверхности начинается при давлении р0, создаваемом воспламенителем. Тогда время достижения стационарного давления можно получить интегрируя указанное дифференциальное соотношение. При этом очевидно можно осуществить разделение переменных в результате чего получится

Считаем, что поверхность горения постоянна и интегрируем до получения давления, которое определяется формулой Бори. При этом следует учесть, что формально получается бесконечное время, но ограничив себя разумными уровнями, например 0.99 получим конечное время достаточно близкое к тому, что наблюдается в реальности.

Sic! Знаменатель обращается в нуль по формуле Бори.

Исходя из посылов использованных при получении формулы Бори рассмотрим как будет происходить изменение давления по времени работы двигателя за счет изменения поверхности горения

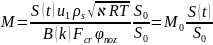и тогда

2. Изменение температуры во внутрикамерном процессе.

Рассмотрим ранее полученное уравнение баланса масс

(3.2.1)

Ранее предполагалось, что температура не меняется во времени. Если отказаться от данного упрощения, то получится

Сделаем допущение о постоянстве химического состава продуктов сгорания, тогда в этом уравнении будет три переменных: давление, температура и время.

Необходимо добавить уравнение энергии для замыкания системы

–полная удельная энергия продуктов сгорания топлива при давлении p и температуре Т.

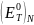– полная удельная энергия топлива при нормальной температуре;

- удельная энтальпия продуктов сгорания топлива, cостав которых определяется при давлении p и температуре Т по данным термодинамического расчета.

секундное изменение тепловых потерь в камере двигателя.

Удельная энтальпия равна сумме удельной внутренней энергии и работы, совершаемой на преодоление внешних сил

В результате

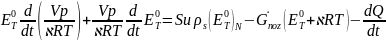
Вычтем из этого уравнения уравнение неразрывности (3.2.1), умноженное на

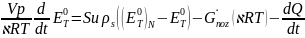
Так как . Если состав неизменен, то

После подстановки получим

Поскольку , то

Снова обратимся к уравнению неразрывности и умножим его на .

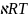Сложив его с (8.106) получим

При этом мы должны знать

Теперь можно выполнить интегрирование этой системы с соответствующими начальными условиями и заданным законом изменения тепловых потерь.

Определение тепловых потерь в простейшем случае можно осуществить исходя из предположения об их постоянстве во времени