3. Модель внутрибаллистического расчета при заряде, составленном из нескольких топлив.

Модель исходит из предположения о возможности осреднения по объему камеры сгорания параметров продуктов сгорания. [1].

S_i, r_{топл i}, , e_i, R_i, b_i, c_pi,k_i, – соответственно поверхность горения, плотность, скорость горения, сгоревшая часть свода, приведенная удельная газовая постоянная, приведенный удельный коволюм, удельная теплоемкость продуктов сгорания, отношение теплоемкостей и полная удельная энтальпия i-го компонента заряда;

Коволюм. Это величина, характерная для определенного типа пороха, пропорциональная объему газовых молекул, и оказывающая влияния на величину давления. При относительно низких давлениях, им можно пренебречь.

равновесная термодинамическая температура продуктов сгорания i-го компонента при давлении р при автономном горении,

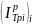– полная удельная энтальпия продуктов сгорания i-го компонента при давлении р и термодинамической температуре ,

– полная удельная энтальпия продуктов сгорания i-го компонента в камере при давлении р и температуре Т;

q_i – массовая доля продуктов сгорания в камере i-го компонента заряда;

N – число компонентов заряда;

q_n+1 – массовая доля начального газа (воздуха) в камере;

- будут обозначены исходные энтальпия, удельная энтальпия при давлении р и температуре Т, удельная газовая постоянная, удельный коволюм, удельная теплоемкость и отношение теплоемкостей воздуха (начального газа);

W, p, r, T, R, b, c_p, k – текущий свободный объем камеры, давление, плотность, температура, удельная энтальпия, удельная приведенная газовая постоянная, приведенный удельный коволюм, удельная теплоемкость и отношение теплоемкостей для всей смеси продуктов сгорания и начального газа в камере двигателя.

Уравнение состояния смеси записывается в виде

Принимая, что отсутствуют реакции между продуктами сгорания компонентов заряда и начального газа можно записать

, ,

Закон сохранения массы всей смеси продуктов сгорания в камере выражается уравнением

(9.3)

Где - секундно-массовый приход в камеру продуктов сгорания i-го компонента заряда; W – текущий свободный объем камеры; G – общий секундно-массовый расход через сопло

Множитель d определяет наличие или отсутствие истечения

определяется моментом (давлением) разрушения мембраны сопла.

Закон сохранения массы продуктов сгорания i-го компонента в камере задается уравнением

(9.6)

Дифференцируя левые части уравнений (9.3) и (9.6) их можно переписать

(9.7)

(9.8)

Увеличение свободного объема камеры происходит за счет сгорания частей заряда, расположенных в этой камере. В случае поступления каких-то компонентов из вне c массовой скоростью и плотностью , то это то же ведет к уменьшению свободного объема камеры. Таким образом, можно записать изменение объема в виде

Индекс определяет момент «подключения» соответствующего компонента i

определяется моментом воспламенения соответствующего топливного сегмента.

Секундно-массовый приход продуктов сгорания G_i от всех компонентов заряда, находящихся в камере и горящих, равен .

Приход от компонентов, которые горят в отдельных объемах, (например воспламенитель в своей коробке) при дозвуковой подаче в камеру можно представить

Где F площадь проходного сечения коробки

Давление в коробке p_jk можно определить

[1] Р.Е. Соркин Теория внутрикамерных процессов в ракетных системах на твердом топливе. Москва, Наука, 1983, с. 288