Значение коэффициента t при разной доверительной вероятности p (распределение Стьюдента)

Число наблюдений n	Значения коэффициента t при доверительной вероятности
	0,90	0,95	0,98	0,99	0,999
2	6,31	12,71	31,82	63,66	636,62
3	2,92	4,40	6,97	9,93	31,60
4	2,35	3,18	4,54	5,84	12,92
5	2,13	2,78	3,75	4,60	8,61
6	2,02	2,57	3,37	4,03	6,87
7	1,94	2,45	3,14	3,71	5,96
8	1,90	2,37	3,00	3,50	5,41
9	1,86	2,31	2,90	3,36	5,04
10	1,83	2,26	2,82	3,25	4,78
11	1,81	2,23	2,76	3,17	4,59
12	1,80	2,20	2,72	3,11	4,44
13	1,78	2,18	2,68	3,06	4,32
14	1,77	2,16	2,65	3,01	4,22
15	1,76	2,15	2,62	2,98	4,14
16	1,75	2,13	2,60	2,95	4,07
17	1,75	2,12	2,58	2,92	4,02
18	1,74	2,11	2,57	2,90	3,97
19	1,73	2,10	2,55	2,88	3,92
20	1,73	2,09	2,54	2,86	3,88
21	1,65	1,96	2,33	2,58	3,29

Практическая работа № 7

Задание 1

Тепловой поток Q(Вт), отводимый от теплообменного аппарата, может быть определён на основе косвенного измерения по формуле

Q=Gс(t_o-t₁) (*),

где G- расход рабочего тела (кг/с),

t_o,t₁—температура рабочего тела на входе и выходе теплообменного аппарата,

c-удельная теплоёмкость рабочего тела (Дж/кг)-является табличной характеристикой.

Величины G,t_o,t₁ -определяются с помощью прямых измерений расхода и температур при с.к.о. погрешностей измерения =0,001 кг/с, =0,1 °С. Вычислить - с.к.о. погрешности измерения Q при с== 4,19.10³ Дж/кг°С, G = 47 кг/с, t₁=12°С, t₂ = 14 °С.

Решение:

Исходим из того обстоятельства, что измеряемые параметры, входящие в формулу (*) статистически независимы. В этом случае дисперсия ² равна сумме дисперсий параметров, измеряемых прямыми методами, умноженных на весовые коэффициенты, равные квадратам частных производных от Q по этим параметрам, т.е.:

найдем частные производные:

Подставим численные значения измеренных величин:

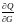=4,19×10³× (14-12)=8,38×10³

=47×4,19×10³=196,93×10³

= -47×4,19×10³= - 196,93×10³

Просуммировав квадраты полученных числовых значений частных производных, умноженных на дисперсии, получим:

=(8,38×10³)²×0,001²+2× (196,9×310³) ײ0,1²=590587274

Или » 24302 (Дж)

Ответ: - с.к.о. погрешности измерения Q равно 24302 Дж.

Варианты заданий

№ варианта по списку	кг/с	°С	t1°С	t2°С	G кг/с
Пример	0,001	0,1	12	14	47
1	0,0011	0,11	13	15	48
2	0,0012	0,12	14	16	49
3	0,0013	0,13	15	17	50
n	0,0011+n×0,0001	0,1+n×0,01	12+№	14+№	47+№

Задание 2

Температура t(°С) может быть оценена с помощью косвенного измерения на основе формулы зависимости величины термосопротивления (ТС) меди R, от температуры в виде

R_t=R_o×( ) (**),

где -температурный коэффициент сопротивления меди,

R_o—величина ТС при 0°С и формулы, связывающей напряжение Uизм, ток Iизм,

R_t и R_л- сопротивление подводящих проводников схемы для ТС:

(***).

Величины Uизм, Iизм, измеряемые вольтметром и амперметром, являются результатом прямых измерений с граничными погрешностями , . Вычислить -граничную погрешность измерения температуры t при Uизм= 7 В, I_изм= 0,67 А, R_л=0,5 Ом, =4,26 10^-3 (°С)^-1.

Решение:

Объединяя формулы (**) и (***), после преобразований получим:

Используем аналог полного дифференциала от функции:

(****)

Определим частные производные от t по U и I:

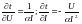
Находим численные значения частных производных и подставляем их в формулу (****):

= 350,36

= -3660,4

= 350,36 × 0,01 + 3660,4 × 0,01= 40⁰С

Ответ: - граничная погрешность измерения температуры t равна 40⁰С.

Варианты заданий

№ варианта по списку	Δu B	Δt A	Uизм В	Iизм А
Пример	0,01	0,01	7	0,67
1	0,011	0,011	7,5	0,7
2	0,012	0,012	8	0,73
3	0,013	0,013	8,5	0,76
n	0,01+n×0,001	0,01+n×0,001	7+n×0,5	0,67+n×0,03

Практическая работа №8