|
|
||||||||||||||||
|
Практическое работа № 1 Расчет шунта для амперметра
Ш 1. Электромагнитный амперметр имеет внутреннее сопротивление Rа , а диапазон измерений. Рассчитайте сопротивление шунта так, чтобы амперметр мог измерять заданный ток (рис. 1,2).
Рис. 1. Рис. 2.
Задачу
решим при помощи первого закона
Кирхгофа:
Кроме
того,
Определить абсолютное значение погрешности измерения тока, если относительная приведенная погрешность прибора равна 1%.
Расчет дополнительного сопротивления для вольтметра |
унтом
называется сопротивление, которое
присоединяется параллельно зажимам
амперметра (параллельно внутреннему
сопротивлению прибора), чтобы увеличить
диапазон измерений. Для увеличения
диапазона измерения какое должен
иметь сопротивление шунт? ( Rш=?).
Если потребитель нужно включить на более высокое напряжение, чем то, на которое он рассчитан, последовательно с ним включают добавочное сопротивление rд (рис. 1, 2). На добавочном сопротивлении создается падение напряженияUд, которое снижает напряжение на потребителе до требуемой величины Uп.
Напряжение источника равно сумме напряжений на потребителе и добавочном сопротивлении: U=Uп + Uд; U=Uп + I x rд. Ток максимального отклонения стрелки индикатора I = 0,001 А
Из этого равенства определить необходимое добавочное сопротивление rд =?
№ варианта по списку |
Uп-Напряжение, которое измеряет прибор |
U -Требуемый предел измерения |
1 |
20 |
30 |
2 |
30 |
40 |
№ п/п |
№ п/п x10+10 |
№ п/п x10+20 |
а) б)
Рис. 1. Добавочное сопротивление Рис. 2. Измерение напряжения
Определить абсолютное значение погрешности измерения напряжения Uп , если относительная приведенная погрешность прибора равна 1%.
Практическая работа № 2
Задание 1
Пример расчета измерений температуры
Результаты
измерений температуры toС
являются случайными величинами,
подчиняющимися нормальному закону
распределения с математическим ожиданием
mt
=
27,1°С и средним квадратичным отклонением
(с.к.о.)
=
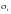0,9 (oС).
Вычислить вероятность выполнения неравенства
to1
t
to2,
где to1=26,1,
oC,
to2=27,85oC.
Решение:
Для решения задачи воспользуемся интегралом вероятностей (функцией Лапласа). Для этого сформируем независимую переменную следующего вида:
И находим соответствующие значения Ф(z1) и Ф(z2).
;
Далее воспользуемся следующим свойством интеграла вероятностей:
Ф(z) = - Ф(z); т.е.
P(t1
t
t2)
= Ф(z2)
- (-Ф(z1));Ф(-z1)
= 1-Ф(z1)
= Ф(z1)
+ Ф(z2)-1
= 0,729
+0,813-1 = 0,542
Ответ: P(t1 t t2) = 0,542
Варианты заданий
№ варианта по списку |
mt °С |
|
to1 °С |
to2 °С |
Пример |
27,1 |
0,9 |
26,1 |
27,85 |
1 |
27 |
0,89 |
26 |
27 |
2 |
26,9 |
0,88 |
25.9 |
26,9 |
n |
27-0,1n |
0,89-0,01 n |
26-0,1 n |
27-0,1 n |
°СПРИЛОЖЕНИЕ
Таблица 1
Значение
функции
(нормированная
функция Лапласа или интеграл вероятности)
Z |
0 |
I |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0,0 |
0,0000 |
0,0040 |
0,0080 |
0,0120 |
0,0160 |
0,0199 |
0,0239 |
0,0279 |
0,0319 |
0,0359 |
0,1 |
0,0398 |
0,0438 |
0,0478 |
0,0517 |
0,0557 |
0,0596 |
0,0636 |
0,0675 |
0,0714 |
0,0753 |
0,2 |
0,0793 |
0,0632 |
0,0871 |
0,0909 |
0,0948 |
0,0987 |
0,1026 |
0,1064 |
0,1103 |
0,II4I |
0,3 |
0,1179 |
0,1217 |
0,1255 |
0,1293 |
0,1331 |
0,1368 |
0,1406 |
0,1443 |
0,1480 |
0,1517 |
0,4 |
0,1555 |
0,1591 |
0,1628 |
0,1664 |
0,1700 |
0,1736 |
0,1772 |
0,1808 |
0,1844 |
0,1679 |
0,5 |
0,1915 |
0,1950 |
0,1985 |
0,2019 |
0,2045 |
0,2088 |
0,2123 |
0,2157 |
0,2I90 |
0,2224 |
0,6 |
0,2257 |
0,2291 |
0,2324 |
0,2357 |
0,2389 |
0,2422 |
0,2454 |
0,2486 |
0,2517 |
0,2549 |
0,7 |
0,2580 |
0,2611 |
0,2642 |
0,2673 |
0,2703 |
0,2734 |
0,2764 |
0,2794 |
0,2823 |
0,2852 |
0,8 |
0,2881 |
0,2910 |
0,2939 |
0,2967 |
0,2995 |
0,3023 |
0,3051 |
0,3078 |
0,3106 |
0,3133 |
0,9 |
0,3159 |
0,3186 |
0,3212 |
0,3238 |
0,3264 |
0,3289 |
0,3315 |
0,3340 |
0,3365 |
0,3389 |
1,0 |
0,3413 |
0,3438 |
0,3461 |
0,3485 |
0,3508 |
0,3531 |
0,3554 |
0,3577 |
0,3599 |
0,3621 |
1,1 |
0,3643 |
0,3665 |
0,3686 |
0,3708 |
0,3729 |
0,3749 |
0,3770 |
0,3790 |
0,3810 |
0,3830 |
1,2 |
0,3849 |
0,3869 |
0,3888 |
0,3907 |
0,3925 |
0,3944 |
0,3962 |
0,3980 |
0,3997 |
0,4015 |
1,3 |
0,4032 |
0,4049 |
0,4066 |
0,4082 |
0,4099 |
0,4115 |
0,4131 |
0,4147 |
0,4162 |
0,4177 |
1,4 |
0,4192 |
0,4207 |
0,4222 |
0,4236 |
0,4251 |
0,4256 |
0,4279 |
0,4292 |
0,4306 |
0,4319 |
1,5 |
0,4332 |
0,4345 |
0,4357 |
0,4370 |
0,4382 |
0,4394 |
0,4406 |
0,4418 |
0,4429 |
0,4441 |
1,6 |
0,4452 |
0,4453 |
0,4474 |
0,4484 |
0,4495 |
0,4505 |
0,4515 |
0,4525 |
0,4535 |
0,4545 |
1,7 |
0,4554 |
0,4564 |
0,4573 |
0,4582 |
0,4591 |
0,4599 |
0,4608 |
0,4616 |
0,4625 |
0,4633 |
1,8 |
0,4641 |
0,4649 |
0,4656 |
0,4664 |
0,4671 |
0,4678 |
0,4686 |
0,4693 |
0,4699 |
0,4706 |
1,9 |
0,4713 |
0,4719 |
0,4726 |
0,4732 |
0,4738 |
0,4744 |
0,4750 |
0,4756 |
0,4761 |
0,4767 |
2,0 |
0,4772 |
0,4778 |
0,4783 |
0,4788 |
0,4793 |
0,4798 |
0,4803 |
0,4808 |
0,4812 |
0,4817 |
2,1 |
0,4821 |
0,4826 |
0,4830 |
0,4834 |
0,4838 |
0,4842 |
0,4846 |
0,4850 |
0,4854 |
0,4857 |
2,2 |
0,4661 |
0,4865 |
0,4868 |
0,487l |
0,4875 |
0,4878 |
0,4881 |
0,4884 |
0,4887 |
0,4890 |
2,3 |
0,4893 |
0,4896 |
0,4898 |
0,4901 |
0,4904 |
0,4906 |
0,4909 |
0,4911 |
0,4913 |
0,4916 |
2,4 |
0,4918 |
0,4920 |
0,4922 |
0,4925 |
0,4927 |
0,4929 |
0,4931 |
0,4932 |
0,4934 |
0,4936 |
2,5 |
0,4938 |
0,4940 |
0,4941 |
0,4943 |
0,4945 |
0,4946 |
0,4948 |
0,4949 |
0,4951 |
0,4952 |
2,6 |
0,4953 |
0,4955 |
0,4956 |
0,4957 |
0,4959 |
0,4960 |
0,4951 |
0,4962 |
0,4963 |
0,4964 |
2,7 |
0,4965 |
0,4966 |
0,4967 |
0,4968 |
0,4969 |
0,4970 |
0,4971 |
0,4972 |
0,4973 |
0,4974 |
2,8 |
0,4974 |
0,4975 |
0,4976 |
0,4977 |
0,4977 |
0,4978 |
0,4979 |
0,4979 |
0,4980 |
0,4981 |
2,9 |
0,4981 |
0,4982 |
0,4982 |
0,4983 |
0,4984 |
0,4985 |
0,4985 |
0,4985 |
0,4986 |
0,4986 |
3,0 |
0,9865 |
0,9869 |
0,9874 |
0,9878 |
0,9882 |
0,9886 |
0,9889 |
0,9883 |
0,8996 |
0,9900 |
3,1 |
0,9903 |
0,9906 |
0,9906 |
0,9912 |
0,9916 |
0,9918 |
0,9921 |
0,9924 |
0,9926 |
0,9929 |
3,2 |
0,9931 |
0,9934 |
0,9936 |
0,9938 |
0,9940 |
0,9942 |
0,9944 |
0,9946 |
0,9948 |
0,9950 |
3 3 |
0,9952 |
0,9954 |
0,9955 |
0,9957 |
0,9958 |
0,9960 |
0,9961 |
0,9962 |
0,9964 |
0,9935 |
3,4 |
0,9966 |
0,9968 |
0,9969 |
0,9970 |
0,9971 |
0,9972 |
0,9973 |
0,9974 |
0,9975 |
0,9976 |
Примеры: I) Z = 0,61; Ф(z) = 0,2291;
2) Z = 3,25; Ф(z) = 0,49942.
Таблица 2
Плотности
вероятности нормального распределения
z |
0 |
I |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0,0 |
0,3989 |
0,3989 |
0,3989 |
0,3988 |
0,3986 |
0,3984 |
0,3982 |
0,3980 |
0,3977 |
0,3973 |
0,1 |
0,3970 |
0,3965 |
0,3961 |
0,3956 |
0,3951 |
0,3945 |
0,3939 |
0,3932 |
0,3925 |
0,3918 |
0,2 |
0,3910 |
0,3902 |
0,3894 |
0,3885 |
0,3676 |
0,3867 |
0,3857 |
0,3847 |
0,3836 |
0,3625 |
0,3 |
0,3814 |
0,3802 |
0,3790 |
0,3778 |
0,3765 |
0,3752 |
0,3739 |
0,3726 |
0,3712 |
0,3697 |
0,4 |
0,3683 |
0,3668 |
0,3653 |
0,3637 |
0,3621 |
0,3605 |
0,3589 |
0,3572 |
0,3555 |
0,3538 |
0,5 |
0,3521 |
0,3503 |
0,3485 |
0,3467 |
0,3448 |
0,3429 |
0,3410 |
0,3391 |
0,3372 |
0,3392 |
0,6 |
0,3332 |
0,3312 |
0,3292 |
0,3271 |
0,3251 |
0,3230 |
0,3209 |
0,3187 |
0,3166 |
0,3144 |
0,7 |
0,3123 |
0,3101 |
0,3079 |
0,3056 |
0,3034 |
0,ЗО11 |
0,2969 |
0,2966 |
0,2943 |
0,2920 |
0,8 |
0,2897 |
0,2974 |
0,2650 |
0,2627 |
0,2803 |
0,2780 |
0,2756 |
0,2732 |
0,2709 |
0,2685 |
0,9 |
0,2661 |
0,2637 |
0,2613 |
0,2589 |
0,2565 |
0,2541 |
0,2516 |
0,2492 |
0,2468 |
0,2444 |
1,0 |
0,2420 |
0,2396 |
0,2371 |
0,2347 |
0,2323 |
0,2299 |
0,2275 |
0,2251 |
0,2227 |
0,2203 |
1,1 |
0,2179 |
0,2155 |
0,2131 |
0,2107 |
0,2083 |
0,2059 |
0,2036 |
0,2012 |
0,1969 |
0,1965 |
1,2 |
0,1942 |
0,1919 |
0,1895 |
,01972 |
0,I849 |
0,1626 |
0,1804 |
0,1781 |
0,1758 |
0,1736 |
1,3 |
0,1714 |
0,1691 |
0,1669 |
0,1647 |
0,1626 |
0,1604 |
0,1582 |
0,1561 |
0,I539 |
0,1518 |
1,4 |
0,1497 |
0,1476 |
0,1456 |
0,1435 |
0,1415 |
0,1394 |
0,1374 |
0,1354 |
0,1334 |
0,1315 |
1,5 |
0,1295 |
0,1276 |
0,1257 |
0,1236 |
0,1219 |
0,1200 |
0,1182 |
0,1163 |
0,1145 |
0,1127 |
1,6 |
0,1109 |
0,1092 |
0,1074 |
0,1057 |
0,1040 |
0,1023 |
0,1006 |
0,0989 |
0,0973 |
0,0957 |
1,7 |
0,0940 |
0,0925 |
0,0909 |
0,0693 |
0,0878 |
0,0663 |
0,0848 |
0,0833 |
0,0818 |
0,0804 |
1,8 |
0,0790 |
0,0775 |
0,0761 |
0,0748 |
0,0734 |
0,0721 |
0,0707 |
0,0694 |
0,0631 |
0,0669 |
1,9 |
0,0656 |
0,0644 |
0,0632 |
0,0620 |
0,0603 |
0,0596 |
0,0584 |
0,0573 |
0,0562 |
0,O551 |
2,0 |
0,0540 |
0,0529 |
0,0519 |
0,0508 |
0,0496 |
0,0488 |
0,0478 |
0,0468 |
0,0459 |
0,0449 |
2.1 |
0,0440 |
0,0431 |
0,0422 |
0,0413 |
0,0404 |
0,0396 |
0,0387 |
0,0379 |
0,0371 |
0,0363 |
2,2 |
0,0355 |
0,0347 |
0,0339 |
0,0332 |
0,0325 |
0,0317 |
0,0310 |
0,0303 |
0,0297 |
0,0290 |
2,3 |
0,0283 |
0,0277 |
0,0270 |
0,0264 |
0,0256 |
0,0252 |
0,0246 |
0,0241 |
0,0235 |
0,0229 |
2,4 |
0,0224 |
0,0219 |
0,0213 |
0,0208 |
0,0203 |
0,0198 |
0,0194 |
0,0189 |
0,0184 |
0,0180 |
2,5 |
0,0175 |
0,0171 |
0,0167 |
0,0163 |
0,0158 |
0,0154 |
0,0151 |
0,0147 |
0,0143 |
0,0139 |
2,6 |
0,0136 |
0,0132 |
0,0125 |
0,0126 |
0,0122 |
0,0119 |
0,0116 |
0,0113 |
0,OIIO |
0,0107 |
2,7 |
0,0104 |
0,0101 |
0,0099 |
0,0096 |
0,0093 |
0,0091 |
0,0088 |
0,0086 |
0,0084 |
0,0081 |
2,8 |
0,0079 |
0,0077 |
0,0075 |
0,0073 |
0,0071 |
0,0069 |
0,0067 |
0,0065 |
0,0063 |
0,0061 |
2,9 |
0,0060 |
0,0058 |
0,0056 |
0,0055 |
0,0053 |
0,0051 |
0,0050 |
0,0046 |
0,0047 |
0,0046 |
3,0 |
0,0044 |
0,0043 |
0,0042 |
0,0040 |
0,0039 |
0,0038 |
0,0037 |
0,0036 |
0,0035 |
0,UU34 |
3,1 |
0,0033 |
0,0032 |
0,0031 |
0,0030 |
0,0029 |
0,0028 |
0,0027 |
0,0026 |
0,0025 |
0,0025 |
3,2 |
0,0024 |
0,0023 |
0,0022 |
0,0022 |
0,0021 |
0,0020 |
0,0020 |
0,0019 |
0,0018 |
0,0018 |
3,3 |
0,0017 |
0,0017 |
0,0016 |
0,0016 |
0,0015 |
0,0015 |
0,0014 |
0,0014 |
0,0013 |
0,0013 |
3,4 |
0,0012 |
0,0012 |
0,0012 |
0,ОО11 |
0,ОО11 |
0,0010 |
0,0010 |
0,0010 |
0,0009 |
0,0009 |
3,5 |
0,0009 |
0,0008 |
0,0008 |
0,0008 |
0,0008 |
0,0007 |
0,0007 |
0,0007 |
0,0007 |
0,0006 |
3,6 |
0,0006 |
0,0006 |
0,0006 |
0,0006 |
0,0005 |
0,0005 |
0,0005 |
0,0005 |
0,0005 |
0,0004 |
3,7 |
0,0004 |
0,0004 |
0,0004 |
0,0004 |
0,0004 |
0,0004 |
0,0003 |
0,0003 |
0,0003 |
0,0003 |
3,8 |
0,0003 |
0,0003 |
0,0003 |
0,0003 |
0,0003 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
3,9 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0002 |
0,0001 |
0,0001 |
Таблица 3
Вероятность Р выхода годных изделий в зависимости от Ψ и E (гауссовский закон распределения)
Ψ |
Е |
||||||||||||||
0 |
0,02 |
0,05 |
0,08 |
0,10 |
0,12 |
0,15 |
0,18 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
|
0,10 |
0,236 |
0,236 |
0,236 |
0,236 |
0,235 |
0,235 |
0,235 |
0,234 |
0,234 |
0,233 |
0,232 |
0,231 |
0,229 |
0,228 |
0,226 |
0,15 |
0,347 |
0,347 |
0,346 |
0,346 |
0,346 |
0 345 |
0,344 |
0,343 |
0,342 |
0,339 |
0,336 |
0,332 |
0,327 |
0,322 |
0,316 |
0,20 |
0,452 |
0,451 |
0,451 |
0,450 |
0,450 |
0,447 |
0,445 |
0,442 |
0,440 |
0,434 |
0,426 |
0,418 |
0,408 |
0,397 |
0,385 |
0,25 |
0,547 |
0,547 |
0,546 |
0,544 |
0,542 |
0,540 |
0,535 |
0,530 |
0,527 |
0,516 |
0,503 |
0,488 |
0,471 |
0,453 |
0,433 |
0,30 |
0,632 |
0,632 |
0,630 |
0 627 |
0,624 |
0,621 |
0,615 |
0,608 |
0,602 |
0,585 |
0,566 |
0,543 |
0,519 |
0,492 |
0 464 |
0,35 |
0,706 |
0,706 |
0,704 |
0 699 |
0,696 |
0,691 |
0,683 |
0,672 |
0,665 |
0,642 |
0,642 |
0,6I6 |
0,554 |
0,519 |
0,482 |
0,40 |
0,770 |
0,769 |
0,766 |
0,761 |
0,757 |
0,751 |
0,740 |
0,727 |
0,718 |
0,696 |
0,657 |
0,620 |
0,579 |
0,536 |
0,492 |
0,42 |
0,792 |
0,792 |
0,789 |
0,783 |
0,778 |
0,772 |
0,760 |
0,747 |
0,736 |
0,706 |
0,671 |
0,631 |
0,588 |
0,542 |
0,494 |
0,45 |
0,823 |
0,823 |
0 819 |
0,813 |
0,807 |
0,801 |
0,788 |
0,773 |
0,762 |
0,729 |
0,690 |
0,646 |
0,599 |
0 549 |
0,496 |
0,48 |
0,850 |
0,849 |
0,846 |
0,839 |
0,833 |
0,826 |
0,813 |
0,796 |
0,784 |
0,749 |
0,707 |
0,660 |
0,608 |
0,554 |
0,498 |
0,50 |
0,866 |
0,866 |
0,862 |
0,855 |
0,849 |
0,842 |
0,828 |
0,811 |
0,798 |
0,761 |
0,718 |
0,668 |
0,614 |
0,559 |
0,499 |
0,55 |
0,901 |
0,900 |
0,896 |
0,889 |
0,883 |
0,874 |
0,860 |
0,842 |
0,828 |
0,789 |
0,741 |
0,687 |
0,628 |
0,565 |
0,499 |
0,60 |
0,928 |
0,927 |
0,923 |
0,916 |
0,910 |
0,902 |
0,887 |
0,868 |
0,854 |
0,812 |
0,761 |
0,704 |
0,640 |
0,571 |
0,499 |
0,65 |
0,949 |
0,948 |
0,944 |
0,938 |
0,931 |
0,923 |
0,908 |
0,890 |
0,876 |
0,833 |
0,781 |
0,720 |
0,651 |
0,577 |
0,500 |
0,70 |
0,964 |
0,963 |
0,960 |
0,953 |
0,947 |
0,940 |
0,926 |
0,907 |
0,895 |
0,852 |
0,799 |
0,736 |
0,663 |
0,583 |
0,500 |
0,75 |
0,976 |
0,975 |
0,972 |
0,966 |
0,961 |
0,954 |
0,941 |
0,924 |
0,911 |
0,869 |
0,816 |
0,750 |
0,671 |
0,589 |
0,500 |
0,60 |
0,984 |
0,983 |
0,98I |
0,975 |
0,971 |
0,964 |
0,952 |
0,937 |
0,925 |
0,885 |
0,832 |
0,764 |
0,684 |
0,595 |
0,500 |
0,85 |
0,969 |
0,988 |
0,987 |
0,982 |
0,978 |
0,973 |
0,962 |
0,948 |
0,937 |
0,899 |
0,846 |
0,778 |
0,695 |
0,601 |
0,500 |
0,90 |
0,993 |
0,992 |
0,991 |
0,987 |
0,984 |
0,979 |
0,970 |
0,958 |
0,947 |
0,911 |
0,859 |
0,891 |
0,705 |
0,606 |
0,500 |
0,95 |
0,996 |
0,995 |
0 994 |
0,992 |
0,988 |
0,985 |
0,977 |
0,966 |
0,956 |
0,923 |
0,873 |
0,804 |
0,716 |
0,612 |
0,500 |
1,00 |
0,997 |
0,997 |
0,996 |
0,994 |
0,992 |
0,989 |
0,982 |
0,973 |
0,964 |
0,933 |
0,885 |
0,816 |
0,726 |
0,618 |
0,500 |
1,05 |
0,998 |
0,998 |
0,997 |
0 996 |
0,994 |
0,992 |
0,986 |
0,978 |
0,970 |
0,942 |
0,896 |
0,828 |
0,736 |
0,624 |
0,500 |
1,10 |
0,999 |
0,999 |
0,998 |
0,997 |
0,996 |
0,994 |
0,989 |
0,983 |
0,976 |
0,950 |
0,906 |
0,839 |
0,745 |
0,629 |
0,500 |
1,15 |
0,999 |
0,999 |
0,999 |
0 998 |
0,997 |
0,996 |
0,992 |
0,986 |
0,980 |
0,958 |
0,9I6 |
0,850 |
0,755 |
0,635 |
0,500 |
1,20 |
0,999 |
0,999 |
0,999 |
0,999 |
0,998 |
0,997 |
0,994 |
0,989 |
0,985 |
0,964 |
0,925 |
0,860 |
0,764 |
0,641 |
0,500 |
1,25 |
0,999 |
0,999 |
0.999 |
0,999 |
0,999 |
0,998 |
0,996 |
0,992 |
0,988 |
0,969 |
0,933 |
0,870 |
0,773 |
0,646 |
0,500 |
1,30 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,997 |
0,994 |
0,990 |
0,974 |
0,940 |
0,879 |
0,783 |
0,652 |
0,500 |
1,40 |
1 |
1 |
1 |
0,999 |
0,999 |
0,999 |
0,999 |
0,998 |
0 996 |
0,988 |
0,964 |
0,911 |
0,796 |
0,674 |
0,500 |
1,50 |
1 |
1 |
1 |
0,999 |
0,999 |
0,999 |
0,999 |
0,998 |
0,996 |
0,988 |
0,964 |
0,917 |
0,816 |
0,679 |
0,500 |
1,60 |
1 |
1 |
1 |
1 |
0,999 |
0,999 |
0,999 |
0,999 |
0,998 |
0,992 |
0,973 |
0,925 |
0,832 |
0,684 |
0,500 |
1,70 |
1 |
1 |
1 |
1 |
I |
0,999 |
0,999 |
0,999 |
0,999 |
0,995 |
0,979 |
0,939 |
0,846 |
0,695 |
0,500 |
I 80 |
1 |
1 |
1 |
1 |
I |
I |
0,999 |
0,999 |
0,999 |
0,996 |
0,985 |
0,947 |
0,860 |
0,705 |
0,500 |
Задание 2
Пример решения
Результаты
измерений температуры t (°С) являются
случайными
величинами
и подчинены нормальному закону
распределения с mt=
20,1oС,
t=0,8
°С. Определить интервал
t,
для
которого с вероятностью p
= 0,79 удовлетворяется неравенство
/t-mt/
t.
Решение:
Используя интеграл вероятностей, находим:
,
Отсюда
обращаясь к таблицам интеграла вероятностей, находим числовое значение аргумента в круглых скобках, т.е.
т.о.
Ответ: интервал t, для которого с вероятностью p = 0,79 удовлетворяется неравенство /t-mt/ t равен 1,432
Варианты заданий
№ варианта по списку |
|
|
p |
Пример |
20,1 |
0,8 |
0,79 |
1 |
20 |
0,79 |
0,78 |
2 |
19,9 |
0,78 |
0,77 |
3 |
19,8 |
0,77 |
0,76 |
n |
20-0,1n |
0,79-0,01 n |
0,78-0,1 n |
,
°С
,
◦C
Практическая работа №3
Задание 1
Измерениям величины у подчинены нормальному закону распределения с математическим ожиданием my и дисперсией y2. Вычислить вероятность выполнения неравенства |y-my| 0,9 y
Решение:
Сформируем случайную величину для функции интеграла вероятностей
По таблицам для интеграла вероятностей по значению
z = 0,1 находим соответствующее значение интеграла вероятностей Ф(z=0,1) = 0,54. Искомая вероятность P = 2Ф(0,1) – 1 = 0,08
Ответ:
Вероятность выполнения неравенства | y-my| 0,1 y равна 0,08.
Варианты заданий
№ варианта по списку |
| вероятность выполнения неравенства |
Пример |
|y-my| |
1 |
0,89 |
2 |
0,88 |
n |
0,89-0,01n |
0,9
y
Задание 2
Пример решения
Результаты
измерений давления р (МПа) являются
случайными величинами, подчинёнными
закону равномерного распределения и
находятся в пределах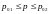
,
где рo1=
1,35 МПа, рo2=
2,6 МПа. Найти математическое ожидание
mp
и дисперсию
для измеренного давления.
Решение:
Формулы для вычисления математического ожидания и дисперсии имеют вид:
Подставив численные значения p1 и p2 получим:
Ответ: Для измеренного давления, математическое ожидание mp = 1,975 и дисперсию = 0,13
Варианты заданий
№ варианта по списку |
рo1 МПа |
рo2 МПа |
Пример |
1,35 |
2,6 |
1 |
1,34 |
2,59 |
2 |
1,33 |
2,58 |
3 |
1,32 |
2,57 |
n |
1,34-0,01n |
2,59-0,01 n |
Практическая работа № 4
Задание 1
Пример решения
Результаты
измерений давления р(Па) являются
случайными величинами и подчинены
закону равномерного распределения с
известными параметрами:
= 0,25 МПа. Вычислить вероятность выполнения
неравенства
po1
p
po2,
где рo1=
1,56 МПа, ро2= 1,69 МПа.
Решение:
Искомая вероятность определяется как отношение площади на графике плотности вероятностей, ограниченной прямыми 1/ (x2 – x1) и р1= 1,56, р2= 1,69 к площади, ограниченной предельными значениями / рo1 и рo2, которые находятся по известным отношениям
и
,
см. рис.
p, Мпа
f(p)
po1 p1 p2 po2
Ответ: вероятность выполнения неравенства po1 p po2 равна 0,08.
№ варианта по списку |
|
рo1 МПа |
po2 МПа |
Пример |
0,25 |
1,56 |
1,69 |
1 |
0,249 |
1,559 |
0,78 |
2 |
0,248 |
1,558 |
0,77 |
n |
0,249-0,1n |
1,559-0,01n |
0,78-0,1 n |
МПа
Задание 2
Термометр, измеряющий температуру t(°С) в рабочем диапазоне от tmin=0°С до tmax= 650°С, имеет класс точности С = 0,6. Определить max- граничную погрешность термометра.
Решение:
Значение приведенной погрешности в соответствии с определением класса точности определяется зависимостью:
Искомое значение граничной абсолютной погрешности определяется по формуле
оС
Ответ: граничная погрешность термометра равна 3,9оС.
Варианты заданий
№ варианта по списку |
Класс точности |
tmax °С |
Пример |
0,6 |
650 |
1 |
0,1 |
200 |
2 |
0,15 |
210 |
3 |
0,2 |
220 |
n |
0,1+0,05n |
200+10 n |
Практическая работа № 5
Задание 1 пример решения
Манометр, измеряющий давление в рабочем диапазоне от pmin=0,05 Мпа до pmax= 2,2 МПа, имеет граничную погрешность p max = 0,055 Мпа. Определить класс точности манометра.
Решение:
Приведенная погрешность манометра выражается следующим образом
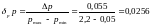
ближайшим
подходящим из стандартного ряда для
величины
*100
=2,56 является число 2,56, что дает основание
считать данный манометр прибором
классности 2,56.
Ответ: манометр является прибором класса точности 2,56.
Варианты заданий
№ варианта по списку |
pmin МПа |
pmax МПа |
|
Пример |
0,05 |
2,2 |
0,055 |
1 |
0,06 |
2,5 |
0,06 |
2 |
0,07 |
2,6 |
0,061 |
n |
0,06+0,01n |
2,5+0,1n |
0,06+0,001 n |
pmax
МПа
Задание 2 Таблица1
Значения ɑ
|
Интервал Δ ɑ
значений ɑ |
Количество попаданий вариант № 1 |
Количество попаданий вариант № 2 |
Количество попаданий вариант № 3 |
6 |
0 – 0,1 |
1 |
2 |
№ |
7 |
0,1 – 0,2 |
3 |
6 |
3Ч№ |
8 |
0,2 – 0,3 |
9 |
18 |
9Ч№ |
9 |
0,3 – 0,4 |
12 |
24 |
12Ч№ |
10 |
0,4 – 0,5 |
15 |
30 |
15Ч№ |
11 |
0,5 – 0,6 |
15 |
30 |
15Ч№ |
12 |
0,6 – 0,7 |
12 |
24 |
12Ч№ |
13 |
0,7 – 0,8 |
9 |
18 |
9Ч№ |
14 |
0,8 – 0,9 |
3 |
6 |
3Ч№ |
15 |
0,9 – 1,0 |
1 |
2 |
№ |
|
|
|
|
|
Построить гистограмму и полигон процесса измерения прибором случайной величины измеряемого параметра ɑ.
Выборка результатов измерения представлена втаблице1
Графическое отображение гистограммы и полигона плотности распределения случайных измерений параметра ɑ представлено на рис 1.
Рис.1 Графическая иллюстрация характера распределения статистического материала есть гистограмма и полигон
Гистограмма распределения строится обычно для интервального изменения значений параметра ɑ. Для этого на интервалах, отложенных по оси абсцисс, строят прямоугольники, высоты которых пропорциональны частотам η, т.е. отношению количества ni попаданий значений ɑ (частостям) в данный интервал Δ ɑ к общему количеству n измерений. На практике чаще пользуются полигоном, который представляет практическую кривую распределения. Для его построения вершины ординат, пропорциональные частотам интервалов, восстановленные перпендикулярно оси абсцисс в точках, соответствующих серединам данных интервалов, соединяют прямыми линиями. Для замыкания кривой крайние ординаты соединяются с близлежащей серединой интервала, в которой частота равна нулю.
По результатам таблицы 1:
1.Построить гистограмму и полигон.
2. Определить доверительную вероятность попадания случайного измерения ɑ в доверительный интервал 0,3 Δ ɑ 0,4
3. Найти значение математического ожидания my выборки