32.5. Довірчий інтервал для ймовірності появи події при малому обсязі вибірки
Нехай кількість незалежних випробувань невелике. В цьому випадку для знаходження границь довірчого інтервалу використовують точну формулу Бернуллі
,
Задамо довірчу ймовірність і знайдемо такі величини та , щоб виконувалось співвідношення
.
Приймемо без доведення, що величина є розв’язком рівняння
, (32.8)
а величина – розв’язком рівняння
. (32.9)
Зауважимо, що в формулах (32.8) та (32.9) є конкретним числом (а не випадковою величиною) випробувань серед незалежних випробувань, в яких відбулася подія .
Існують
спеціальні таблиці для знаходження
чисел
та
,
що задовольняють рівнянням (32.8) та (32.9)
по заданим величинам
,
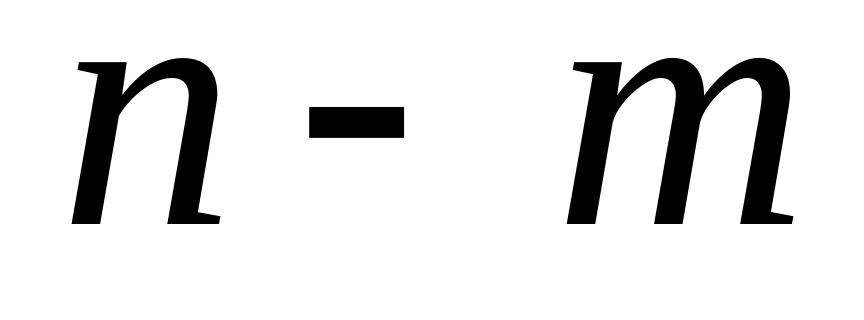та
.
32.6. Довірчий інтервал для параметру в законі Пуассона
Розглянемо
вибірку
із закону Пуассона з параметром
.
За точкову оцінку параметра
доречно взяти вибіркове середнє
,
оскільки математичне сподівання
.
При великому обсязі вибірки вибіркове
середнє розподілено за нормальним
законом
.
Таким чином, статистика
має наближено стандартний нормальний розподіл .
Користуючись таблицею значень функції Лапласа, для заданої довірчої ймовірності знайдемо таке число , при якому
. (32.10)
Розв’язуючи
цю нерівність відносно величини
,
отримаємо
,
де
.