27.3. Графічне зображення вибірки

Для графічного зображення варіаційних рядів найчастіше використовують полігон частот (полігон відносних частот), гістограму частот та кумулятивну криву. Графічне зображення рядів дозволяє отримати наглядне уявлення про закономірності варіювання спостережених значень випадкової величини .

Означення 27.7. Полігоном частот називається ламана з вершинами у точках , , а полігоном відносних частот – ламана з вершинами в точках , . Полігон частот (полігон відносних частот) використовують для зображення дискретного варіаційного ряду.

Гістограму частот використовують для зображення інтервального варіаційного ряду.

Означення 27.8. Гістограмою частот називається ступінчата фігура з прямокутників із основами, які дорівнюють , та висотами . Аналогічно визначають гістограму відносних частот, тільки висоти прямокутників беруть , . Площа відповідної ступінчатої фігури для неї дорівнює одиниці.

Площа ступінчатої фігури під графіком гістограми дорівнює об’єму вибірки . Площа відповідної ступінчатої фігури під графіком гістограми відносних частот дорівнює одиниці. Отже, гістограма відносних частот, якщо відомо, що випадкова величина неперервна, є аналогом графіку щільності розподілу цієї випадкової величини.

Означення 27.9. Кумулятивною кривою (кумулятою) називається крива накопичених частостей.

Для дискретного варіаційного ряду кумулята є ламана, яка з’єднує точки або , а для інтервального варіаційного ряду ламана починається з точки, абсциса якої дорівнює початку першого інтервалу, а ордината – накопленій частоті (або частості). Інші точки цієї ламаної відповідають кінцям інтервалів.

Приклад 27.6. Побудувати полігон і гістограму відносних частот (рис. 27.1 і рис. 27.2), користуючись даними табл. 27.3.

Розв’язання. Відповідні зображення вибірки приведені на рис. 27.1 і рис. 27.2.

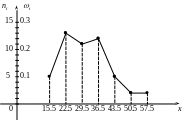
Рис. 27.1.

Рис. 27.2.

27.4. Емпірична функція розподілу

Як відомо, закон розподілу будь-якої випадкової величини можна задавати функцією розподілу . Якщо мати вибірку значень цієї випадкової величини, то можна побудувати деяке наближення функції розподілу.

Означення 27.10. Емпіричною функцією розподілу називається функція розподілу дискретної випадкової величини, що набуває значення варіант з ймовірністю , тобто:

(27.3)

де = , тобто накопичена частість.

Очевидно, що при і при . На проміжку є неспадною кусково-сталою функцією.

Аналогічно визначається емпірична функція розподілу для інтервального варіаційного ряду. Оскільки, ми маємо лише значення емпіричної функції на кінцях інтервалів, то для графічного її зображення доцільно до визначити , з’єднав точки графіка, які відповідають кінцям інтервалів, відрізками прямої. В результаті отримана ламана співпаде з кумулятою.

Приклад 27.7. Побудувати емпіричну функцію розподілу вибірки, що представлена інтервальним варіаційним рядом прикладу 27.5.

Розв’язання. Для побудови графіка емпіричної функції розподілу використаємо формулу (27.3) та значення табл. 27.3.

Рис.27.3.

Із теореми Бернуллі випливає, що емпірична функція розподілу при прямує за ймовірністю до функції розподілу . Крім того, візьмемо до уваги теорему Глівенко - Кантеллі, згідно якої, при із ймовірністю 1 рівномірно відносно х.

246