Тема 6. Математична статистика

ЛЕКЦІЯ 27

ВИБІРКА ТА ЇЇ ГРАФІЧНЕ ЗОБРАЖЕННЯ

Питання, що розглядаються в лекції

1. Генеральна сукупність і вибірка.

2. Первинна обробка статистичних даних.

3. Графічне зображення вибірки.

4. Емпірична функція розподілу.

Вступ

Математична статистика – це наука, що займається вивченням випадкових величин або випадкових подій за результатами дослідних даних. При цьому вважається, що до дослідів можна застосувати теоретико-ймовірнісні концепції. Математична статистика виникла в XYII сторіччі та розвивалася паралельно з теорією ймовірностей. Великий внесок у розвиток цієї науки внесли П.Л.Чебишев, А.А. Марков, А.М.Ляпунов та інші. Задачі математичної статистики можна формулювати з різною мірою загальності, але до найбільш важливих відносяться: оцінювання параметрів розподілів, побудова оцінок параметрів розподілів за дослідними даними, перевірка статистичних гіпотез.

27.1. Генеральна сукупність і вибірка

Розглянемо стохастичний експеримент, в якому спостерігається випадкова величина . Імовірнісною моделлю експерименту є трійка , де – множина всіх можливих значень випадкової величини випадкової величини, – -алгебра числової множини , – функція розподілу випадкової величини . Зробив незалежних повторень експерименту отримаємо послідовність значень випадкової величини , які позначимо ... , . Кожен член цієї послідовності належить множині випадкової величини .

Означення 27.1. Множина називається генеральною сукупністю, послідовність називається вибіркою, кількість елементів вибірки називається обсягом вибірки. Простір , в якому вибірка набуває значень називається вибірковим простором.

При побудові імовірнісної моделі експерименту вважають:

1) вибірка вважається репрезентативною, тобто для всіх елементів із генеральної сукупності існує одна й та ж ймовірність бути включеними у вибірку. Репрезентативність вибірки забезпечується випадковістю відбору, при цьому вважаємо, що генеральна сукупність не змінюється при вилученні якогось елемента вибірки. Це означає, що здійснюється вибір з поверненням. Вибірки, які є репрезентативними, з точки зору генеральної сукупності, можна вважати випадковими вибірками;

2) числова послідовність є реалізацією -вимірного випадкового вектора . Компонента , цього випадкового вектора є значенням випадкової величини при -му спостереженні. Будемо вважати, що компоненти є незалежними у сукупності випадковими величинами, оскільки послідовні вилучення з генеральної сукупності незалежні. Крім того вони всі мають одну й ту ж саму функцію розподілу, тобто . Отже, закон розподілу випадкового вектора повністю визначається формулою

.

Якщо вважати, що генеральна сукупність має неперервний закону розподілу імовірностей з щільністю розподілу , то щільність розподілу вибіркового вектору має вигляд

. (27.1)

Якщо ж генеральна сукупність має дискретний закон розподілу з рядом розподілу , , то розподіл випадкового вектора задається ймовірностями

. (27.2)

Означення 27.2. Функція , яка має вигляд (27.1) для неперервного розподілу генеральної сукупності та вигляд (27.2) у дискретному випадку називається функцією правдоподібності випадкової величини .

Приклад 27.1. Знайти функцію правдоподібності нормально розподіленої генеральної сукупності із параметрами та за реалізацією вибірки .

Розв’язання. За означенням 27.1 функції правдоподібності та формулою (27.1) маємо

.

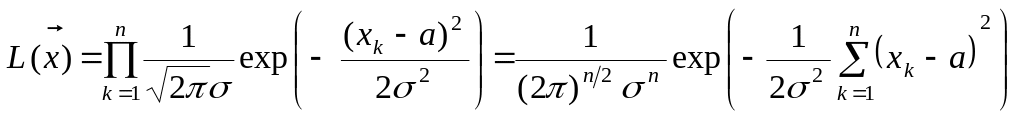Приклад 27.2. Знайти функцію правдоподібності рівномірно розподіленої генеральної сукупності на проміжку за реалізацією вибірки .

Розв’язання. Оскільки

то за означенням 27.1 функції правдоподібності та формулою (27.1) маємо

для всіх , . Отже, функція правдоподібності в цьому випадку не залежить від вибіркового вектора.

Приклад 27.3. Знайти функцію правдоподібності генеральної сукупності , розподіленої за законом Пуассона з параметром за реалізацією вибірки .

Розв’язання. За означенням 27.1 функції правдоподібності та формулою (27.2) маємо

.

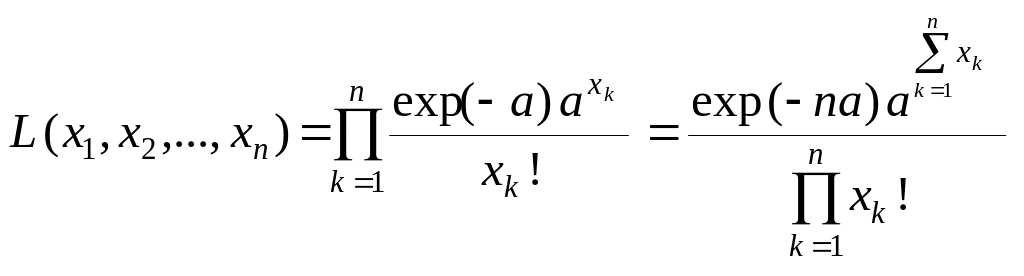Таким чином, в математичній статистиці розглядають випадкові вибірки обсягом із генеральної сукупності з функцією розподілу , тобто результати експериментів є незалежними у сукупності випадковими величинами з однією функцію розподілу.