Проблема взаимодействия подцелей.

Пример:

Мир роботов и кубиков.

X = {A, B, C, …} – множество кубоиков.

H = {1, 2, …} - множество рук.

CL(x) - кубик х свободен (на него можно ставить).

ON(x,y) - кубик х стоит на у.

ONT(x) - кубик х на столе.

HE(k)ё - к-тая рука робота свободна.

HL(x, k) - в к-той руке робота находится кубик.

Продукция имеет вид:

Левая часть = условие применимости продукции,

Правая часть = список дополнения (истинные предикаты) и список исключения (ложные предикаты).

P1(x, k) - взять кубик х со стола.

P1(x, k) = (ONT(x)&CL(x)&HE(k))

HL(x,k)& ONT(x)&CL(x)&HE(k)

P2(x, k) - поставить кубик х на стол рукой к.

P2(x, k) = (HL(x, k))

ONT(x)&CL(x)&HE(x)& HE(x, k)

P3(x, y, k) - поставить кубик х на кубик у к-той рукой.

P3(x, y, k) = (HL(x, y, k)&CL(y))

ONT(x, y)&CL(x)&HE(k)& HL(x, k)&CL(y)

P4(x, y, k) - снять кубик х с кубика у к-той рукой.

P4(x, y, k) = (HE(k)&ON(x, y)&CL(x))

CL(y)&HE(x, k)& HE(k)&CL(x)&ON(x, y)

Последовательная реализация целей. (однорукий робот).

A

С

C

А

B

B

SнSк

Sк = (ONT(B), ON(C, B), ON(A, C), CL(A), HE)

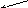
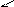
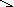
ONT(B) ON(C,B) ON(A, C) CL(A) HE

+ + +

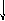P3(A, C)

P3(C, B)

P1(C)

CL(B)

HL(C)

CL(C)

HL(A)

P1(A)

P4(A, X)

+

P4(C, X)

CL(C)

HE

ONT(C)

ON(C,X)

CL(C)

HL(C)

CL(C)

HE

ONT(C)

ON(C,X)

CL(C)

HL(C)

+

+ + - + (X=A) + + + + - + (X=A) +

• ON(C, B): P4(C, A), P3(C, B)

ON(A, C): P1(A), P3(A, C)

Решение: P4(C, A), P3(C, B), P1(A), P3(A, C)

Параллельная реализация подцелей. (двурукий робот)

1. Независимые подцели. n одноруких роботов.

2. Зависимые подцели.

А

С

B

B

C

A

SнSк

ON(C, B), ON(A, C)

ON(C, B)

ON(A, C)

P4(C, A, 1, P3(C, B, 1)

P3(A, C)

HL(A, 2)

CL(C)

+

P1(A, 2)

P1(A,X,2)

HE(2)

ONT(A)

CL(A)

+ +

P2(C, 2)

P1(C,A,2)

P4(X,A,2)

HL(2)

ON(X,A)

CL(X)

+ + (X=C) + (X=C)

P4(C, A, 2) t1 P2(C, 2) t3 P1(A, 2) t4 P3(A, C, 2)

Рука 2 t

P4(C, A, 1) t1 P3(C, B, 1) t2

Рука 1 t

Согласование подцелей.

1. Супервизор. (Следит за процессом и строит реальный план.)

P1(A, 2) t3 P3(A, C, 2) t4

Рука 2t

P4(C, A, 1) t1 P3(C, B, 1) t2

Рука 1t

Итоговое решение:

P4(C, A, 1), P3(C, B, 1) || P1(A, 2), P3(A, C, 2)

Последовательное выполнение: t = t4 + t3 + t1 + t2

Параллельное выполнение: t = t4 + max(t3, t1) + t2

2. Частично упорядоченные подцели.

P4(C, A, 1)

P3(C, B, 1)

P1(A, 2)

P3(A, C, 2)

ON(C, B), ON(A, C)

P3(A, C, 2)

ON(C, B)&CL(C)&HL(2)

ON(1, B)&CL(1)

HL(A, 2)

P1(A, 2)

P3(C, B, 1)

HE(2)&CL(C)&ONT(A)

HL(1, 1)&CL(B)

HL(C, 1)&CL(B)&HE(2)&CL(A)&ONT(A)

P4(C, A, 1)

HE(1)&CL(C)&ON(C, X)

Таблица решений:

ТР	P1	P2	…	Pn
ONT(X)	1	(0)
HE	1	(0)
ON(X, Y)	(0)	(0)
CL(X)	1	(0)
HL(X)		1
ONT(X)	0	1
HE	0	1
ON(X, Y)
CL(X)		1
HL(X)	1	(0)