2. Критерии сравнимы.

1. Метод выделения главного критерия

Пусть имеется главный критерий .Тогда решаем задачу

В этом случае может оказаться, что решения не существует. Тогда нужно

ослабить требования -

2. Метод последовательных уступок.

1 шаг

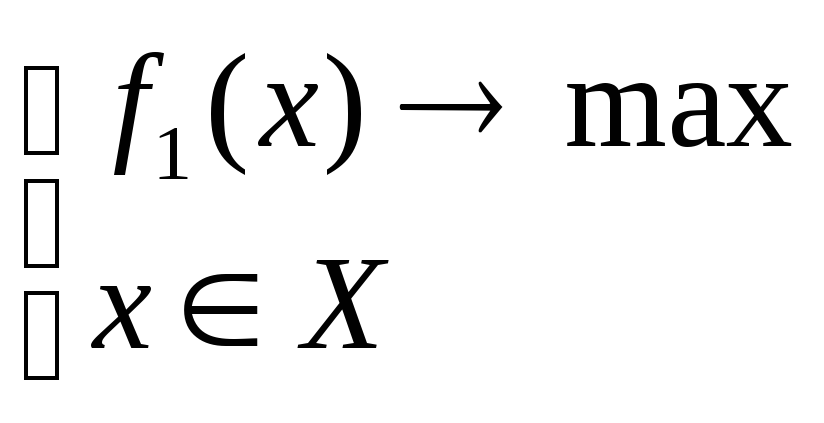- получим решение

2 шаг

………………………

n шаг

Если решение существует, то возможны 2 случая:

a). Решение устраивает ЛПР

b). Решение не устраивает ЛПР:

- решение единственное

- решение не единственное

Проблема сокращения поискового пространства

1). Сочетание точных и грубых методов.

Грубые методы - сокращают область поиска решения

Точные методы - ищут оптимальное решение.

2). Использование эвристических функций.

3). Человеко-машинные процедуры поиска оптимального решения.

1). ЛПР задает начальное значение опорного плана и весовых коэффициентов

- скорость изменения решения по i-му критерию.

2). Коректир.

Поиск решения в пространстве состояний на основе эвристической функции

Задача эвристического поиска

, где

S – множество состояний;

- множество допустимых состояний;

- множество начальных состояний;

- множество конечных состояний;

- множество преобразований.

Задача: нахождение последовательности преобразований :

Система поиска

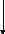
Недетерминированный выбор

Оценка альтернатив и выбор альтернативы

Реализация

+

U-ветвление. Вводится предикат P, определенный на множестве ,который имеет значение истина, если это ветвление может быть применено.

U- ветвление корректно 

Способы сокращения поискового пространства

1). Укрупнение пространства поиска. Переход от элементарных состояний к

макросостояниям.

Проблема поиска решается в укрупненном пространстве.

2). Использрвание эвристик.

3). Изменение представления задачи.

Пример

Вопрос: сколько ходов нужно сделать, чтобы поменять коней местами.

1	2	3
4	5	6
7	8	9

Ответ: 16 ходов (4 – если разрешить им передвигаться || )

Поиск решения на основе эвристической функции.

Допустимый алгоритм – это тот алгоритм, который гарантирует отыскание решения.

Оптимальный алгоритм – это допустимый алгоритм, который находит решение за минимальное число шагов.

f(s) = f₁(s) + f₂(s) -> min

f₁(s) – оценка пройденного пути.

f₂(s) – оценка оставшегося пути.

_ _ _

f(s) = f₁(s) + f₂(s) -> min

_ _

f₂(s) f₂(s)

Теорема.

_ _

f₂ ^А1(s) f₂ ^А2(s)

Чтобы алгоритм, построенный на основе эвристической функций f был допустим, необходимо и достаточно, что .

Алгоритм А1 более информирован, чем А2 