7.4. Дифференцирование сложных функций

Пусть для функции n - переменных аргументы являются также функциями переменных :

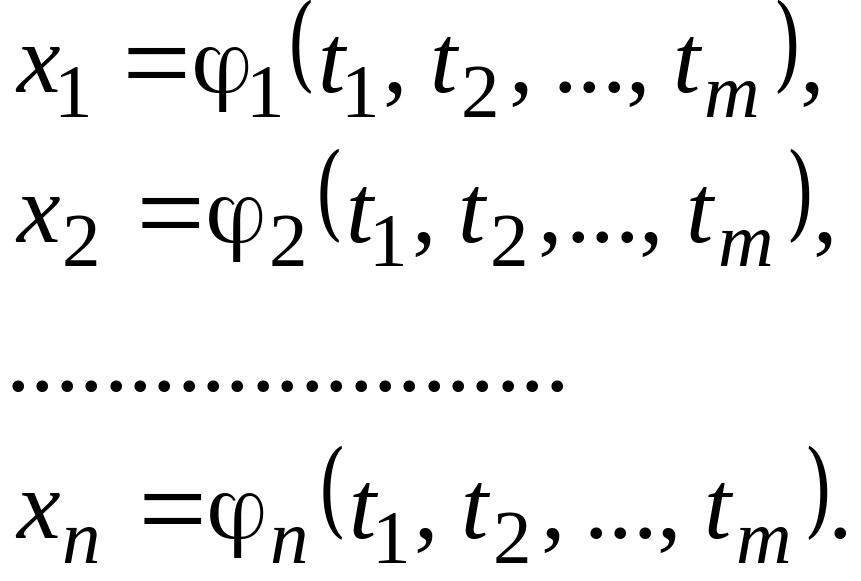(12)

Справедлива следующая теорема о дифференцировании сложной функции.

Теорема 8. Если функции дифференцируемы в точке , а функция дифференцируема в соответствующей точке , где , . Тогда сложная функция дифференцируема в точке , причем частные производные определяются по формулам

где частные производные вычисляются в точке , а вычисляются в точке .

 Докажем эту теорему для функции двух переменных. Пусть , а .

Пусть и произвольные приращения аргументов и в точке . Им соответствуют приращения функций и в точке . Приращениям и соответствует приращение функции в точке . Так как дифференцируема в точке , то ее приращение может быть записано в виде

, (13)

где и вычисляются в точке , при и . В силу дифференцируемости функций и в точке , получаем

(14)

где вычисляется в точке ; .

Подставим (14) в (13) и перегруппируем слагаемые

.

Заметим, что при , так как и стремятся к нулю при . Это следует из того, что бесконечно малые при и . Но функции и дифференцируемы, а, следовательно, и непрерывны в точке . Поэтому если и , то . Тогда и при .

Так как частные производные вычисляются в точке , то получаем

.

Обозначим

(15)

Тогда

,

а это и означает, что дифференцируема по переменным и , причем

и . 

Следствие. Если , причем , , т.е. , то производная по переменной t вычисляется по формуле

.

Если , то

.

Последнее выражение называется формулой полной производной для функции многих переменных.

Примеры. 1) Найти полную производную функции , где , .

Решение.

= .

2) Найти полную производную функции , если , .

Решение.

.

Используя правила дифференцирования сложной функции, получим одно важное свойство дифференциала функции многих переменных.

Если независимые переменные функции , то дифференциал по определению равен:

. (16)

Пусть теперь аргументы есть дифференцируемые функции в некоторой точке функции по переменным , а функция дифференцируема по переменным , . Тогда можно рассматривать как сложную функцию переменных , . Она по предыдущей теореме дифференцируема и имеет место соотношение

, (17)

где определяется по формулам (12). Подставим (12) в (17) и, собирая коэффициенты при , получим

.

Поскольку коэффициент при производной равен дифференциалу функции , то для дифференциала сложной функции получили снова формулу (16).

Таким образом, формула первого дифференциала не зависит от того, являются ли ее аргументы функциями, или они независимыми. Это свойство называют инвариантностью формы первого дифференциала.