Раздел 2 Линейные автоматические системы управления

Передаточные функции замкнутых систем.

x

W(P)

(t) y(t) -блок-схема одноконтурной системы с обратной связью

β(P)

W(Р)- передаточная функция прямой связи

r(t) β(Р) – передаточная функция обратной связи.

Выходной согнал Х(t) складывается с сигналом обратной связи r(t).

Их сумма воздействует на прямую цепь и вызывает на выходе

Wс(Р)=У(Р)/Х(Р) = W(Р)/[1-β(Р)W(Р)]

Передаточная функция замкнутой системы.

Структурная схема отражает математическое преобразование сигналов.

Целью преобразования структурной схемы является получение уравнения системы, связывающее выходную и входную величины.

Структурная схема упрощается путем замены соединения звеньев эквивалентными звеньями, передаточные функции которых находятся по определённым формулам.

В практике встречаются структурные схемы, содержащие перекрёстные связи. Эти схемы с помощью правил переноса могут быть приведены в комбинации соединений.

Основные правила переноса:

1.Перенос сумматора через звено:

а) по направлению передачи воздействия

б) против направления передачи воздействия.

2. Перенос узла разветвления через звено( по направлению и против)

3. Перенос узла разветвления через сумматор ( по направлению и против направления)

4

Wu

. Рядом расположенные узлы разветвления ( сумматоры) можно менять местами между собой или объединять в один. U

Wnc

Wu

U1 y

Woc

Yoc

Передаточная функция одноконтурной замкнутой системы, равна дроби, в числителе которой записывается передаточная функция прямого пути между входом и выходом, а в знаменателе- увеличенная на 1 передаточная функция разомкнутой системы.

W= Wп*Wи*Wос

1. Основная передаточная функция –W= Wп*Wи/1+WпWиWос

2. Передаточная функция по возмущению Wub=Wu/1+W

3. Передаточная функция по задающему воздействиюWа= 1/1+W

4. Передаточная функция по возмущению относительно рассогласования

Wue=-Wu*Woc/1+W

W1(P)

I II

Х

W3(P)

W4(P)

вх

W2(P)

W6(P)

W5(P)

III

Первое и второе звено объединены в блок I с параллельно-согласованным соединением.

5 и 6 – в блок III с последовательным соединением

В блок II выделено 4 звено, охваченное собственной обратной связью (+)

Передаточные функции блоков.

WI (P)=W1+W2 ; WII (P)= W4(P)/ 1- W4(P)*1 ; WII(P)= W5 (P)*W6(P)

В свою очередь 1 блок и третье звено и второй блок соединены последовательно, а 3 блок включен в цепь (-) обратной связи.

Wсау(Р)=[W1(Р)+W2(Р)]*W3(Р)*W4(Р)/1-W4(Р)/

1+[W1(Р)+W2(Р)]W3(Р)*W4(Р)/1-W4(Р)*W5(Р)*W6(Р);

Устойчивость систем автоматического управления.

Устойчивость системы- свойство возвращаться к состоянию установившегося равновесия после устранения возмущения, нарушившего равновесие.

Устойчивость является необходимым условием работоспособности систем.

С истема неустойчива, если после снятия возмущения выходная величина неограниченно удаляется от первоначально установившегося режима ( удаление может быть монотонным или в виде расходящихся колебаний).

у У уст(t)

Если график переходного процесса сходящийся, то система устойчива, а если расходящийся, то неустойчива.

0 tУстойчивость не бывает частичной. Она либо есть,- либо её нет.

При проектировании и эксплуатации систем управления одним из основных требований является требование устойчивости системы. Устойчивость не зависит от величины возмущения. Если система устойчива при малых возмущениях, то она устойчива и при больших.

Для суждения об устойчивости системы достаточно исследовать и определить устойчивость в малом, т.е. найти устойчивость, описываемую дифференциальным уравнением.

Нелинейные системы, описываемые нелинейными дифференциальными уравнениями, могут быть устойчивыми при малых возмущениях и не устойчивыми при больших.

- чтобы система была устойчивой, то петлевое усиление должно находиться в пределах -∞<k=kд*kβ<1

- условием статической устойчивости линейных систем является отсутствие у знаменателя передаточной функции системы корней с положительной действительной частью.

- для устойчивости необходимо, чтобы знаки всех коэффициентов знаменателя её передаточной функции были одинаковы (только для звеньев 1и2 порядков).

Чтобы разомкнутая система оказалась неустойчивой - достаточно одного неустойчивого звена.

Критерии устойчивости

На практике для определения устойчивости используют критерии устойчивости, т.е. правила, с помощью которых можно определить устойчивость системы, не прибегая к решению дифференциальных уравнений.

Алгебраический (по Лапунову) (Рауса_ Гурвица)- позволяет судить об устойчивости замкнутой системы по коэффициентам её характеристического уравнения, которым является знаменатель передаточной функции, т.е. требуют выполнения алгебраических операций над коэффициентом уравнения.

Система будет неустойчивой, если имеется хотя бы один положительный вещественный корень или хотя бы один комплексный корень с «+»,значением вещественной части. (отсутствует «0» и «-» коэффициент). Для систем невысокого порядка применяется.

Частотный метод- основан на построении тех или иных частотных характеристик. Общей базой для критериев служит принцип аргумента.

Этот принцип позволяет по изменению аргумента комплексной функции частоты определить распределение корней уравнения относительно мнимой оси.

Практическое применение – построение годографа вектора A(jω) при 0≤ ω ≤∞ и определение изменения угла поворота обеспечивает наглядность инженерных расчетов.

Метод облегчает процесс исследования устойчивости одновременно с исследованием качества процесса.

Оценивать расположение годографа относительно точки (-1;0)

Критерий устойчивости:

1. Если система устойчива, то годограф не должен охватывать точки с координатами (-1;0).

2. Если не устойчива и имеет Kкорней справа от мнимой оси, то W(jω) приW -∞ до+∞ должна охватывать точку (-1;0) K раз.

При отрицательном знаке y W(j ω) устойчивость определяется точкой (+1;0)

J J J

-устойчивые

( -1;0) ω =∞ ω =0 Re (-1;0) Re Re

точка(-1;0)называется критической.

Этот метод называется так же критерий устойчивости Найквиста или амплитудно-фазовый критерий.

Метод графически нагляден и позволяет оценить запасы устойчивости; легко оценить влияние параметров отдельных звеньев на устойчивость системы; оценить характер переходного процесса.

Критерий устойчивости Михайлова.

Этот критерий относится к частотным. Критерий основан на связи характера переходного процесса системы с амплитудой и фазой вынужденных колебаний, устанавливающихся в системе при синусоидальном воздействии.

Анализ сводится к построению по знаменателю передаточной функции комплексной частоты функции, по виду которой можно судить об устойчивости системы.

Задавая различные значения ω и откладывая Rе (ω) по горизонтале ,а Jm(ω) по вертикале , можно построить кривую, называемую годографом характеристического вектора или кривой Михайлова.

Чтобы составить представление о свойствах кривой Михайлова,определим точки пересечения её с осями, возможные «max» и «min», предельные значения при ω ≥0.

Критерий Михайлова – для устойчивости необходимо, чтобы вектор при изменении частоты от 0 до∞ повернулся в положительном направлении ( нач. с + вещественной оси) на число квадрантов, равное порядку исходного уравнения ( не проходит через начало координат).

Если последовательность прохождения квадрантов нарушена, то система не устойчива,

Критерий Михайлова целесообразен при исследовании сложных многоконтурных систем уравнения.

Jm САУ -устойчива

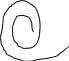
Re

n=8

Запас устойчивости по амплитуде и фазе.

Запас устойчивости - это величины, которые количественно характеризуют удаление устойчивой системы от границы её устойчивости.

1. По амплитуде ΔL, есть число децибел на которые нужно увеличить коэффициент усиления по частоте, соответствующей фазовому сдвигуφ=-π, чтобы система потеряла устойчивость.

На ЛАЧХ ΔL- отрезок между осью абсцисс и ординат при частоте, соответствующей фазовому сдвигу –π

Запас устойчивости по модулю вектора - величина, показывающая во сколько раз необходимо изменить передаточный коэффициент системы при неизменных остальных параметрах, чтобы устойчивая система оказалась на границе устойчивости.

2. По фазе – величина, показывающая на сколько нужно уменьшить (увеличить) фазу, не изменяя амплитуды, чтобы ранее устойчивая система оказалась на границе устойчивости.

Запас можно определить по АФХ, если с центром в начале координат провести окружность единичного радиуса и определить её точку пересечения с АФХ.

Н а практике ɣ= 10÷30˚; Δφ≥(30÷60.

L ,φ J

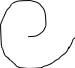-L(w)

0 wnw -1 k>1 R

Wc ΔL

-π/2_ _ _ _ _ _ _ _ _ _ ɣ w φ(w)<0

- π _ _ _ _ _ ɣ_ _ _ _ _ wc

-3/2π _ _ _ _ _ _ _ _ _ _ _ - φ(w)

При построении ЛАЧХ помнить, что каждое звено дает сдвиг по фазе.

Область устойчивости.

Областью устойчивости называется замкнутая или не замкнутая область в пространстве варьируемых параметров, каждой точке которой соответствует устойчивое состояние системы.

Система называется структурно-устойчивой, если её можно сделать устойчивой без изменения структуры при некоторых положительных вещественных значениях её параметров.

Изменение структуры – это добавление или изъятие некоторых звеньев.

Стабилизацией называется придание системе устойчивости.

Два вида стабилизации:

а) параметрическая (за счет изменения параметров);

б) за счет корректирующих устройств.

Анализ устойчивости.

1. Система состоит из “n” последовательно включенных апериодических и колебательных звеньев, то уменьшением передаточного коэффициента можно придвинуть начало годографа Михайлова при ω =0 к началу координат настолько, чтобы оно попало внутрь первого витка годографа, при этом система будет устойчива.

2. Система с интегрирующими звеньями, то АФХ приближается к точке (1;0), что вызывает ухудшение устойчивости, но можно подобрать малый передаточный коэффициент для улучшения устойчивости.

3. Система с запаздывающим звеном будет устойчивой, если время запаздывания τ такова, что ω τ меньше 0, то годограф вектора Wτ(j ω) не охватит точку (-1;0); если τ ω =0, то годограф пройдут через τ(-1;0) и система находится на границе устойчивости. Если ω τ>0, то система будет неустойчивой.

Способы повышения устойчивости :

а) введение в систему дифференциального звена

б) охват звеньев обратными связями.

Заключение :

1. Устойчивость является важнейшим качественным свойством и определяет работоспособность системы.

2. Устойчивость определяется её собственными свойствами и не зависит от внешних факторов. Для анализа используются критерии устойчивости (алгебраический, частотные Михайлова. Найквиста, Вышнеградского, Гурвица).

3. При проектировании необходимо проверять запас устойчивости.

Качество систем автоматического управления.

Для работоспособности системы недостаточно выполнения одного лишь требования устойчивости. Устойчивая система должна иметь высокие показатели качества:

1. Малую установившуюся ошибку регулирования т.е. высокую точность.

2. Малую длительность переходных процессов, т.е. высокое быстродействие.

3. Малую колебательность переходных процессов, т.е. высокую плавность их протекания.

Качество регулирования определяется по ошибке регулирования, т.е. именно ошибка, как функция времени, определяет все три перечисленных показателя качества

Ошибка регулирования- это разность между заданным и действительным значениями регулируемой величины.

Качество САР следует оценивать отдельно по задающему и возмущающему воздействиям. При этом показатели качества должны отвечать заданным требованиям.

Качество процесса регулирования определяют прямыми и косвенными методами.

Типовые воздействия и виды установившихся ошибок.

1. Постоянное (ступенчатое) Ао= const - соответствующая ему установившаяся ошибка называется статической; δ уст= δст.

2. Линейно-изменяющееся воздействие Ао=А1*t- ошибка скоростная; δ уст= δск.

3. С постоянным ускорением – ошибка по ускорению;δ уст= δуск.

4. Полиноминальные ( квадратичные)- динамические δ уст= δдин.

5. Гармоническое Amsin(wt+φ)- динамические

Для определения показателей качества нужно изучить поведение системы в переходном процессе.Возмущающее воздействие должно наиболее полно характеризовать свойства системы. Наиболее часто выбирают единичное возмущение при нулевых начальных условиях.

Прямые показатели качества:

Их удобно использовать, когда имеется график переходного процесса, который может быть получен экспериментально в реальной системе регулирования или путем моделирования на ЭВМ.

1. Статическая ошибка-это разность между установившемся значением регулируемой величины и её заданным значением.

σ 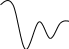(t) σ(t) σ(t)

t t t

без перерегулирования с перерегулированием большая колебательная

Большая колебательность может вывести из строя механическое регулирующее устройство. Ошибка зависит от сухого трения, зазоров и т.д.

2. Динамическая ошибка - наибольшее отклонение регулируемой величины от её установившегося значения.

3. Время регулирования, за которое разность между текущим значением регулируемой величины и её заданным значением становится меньше 5% от заданного значения.

4. Перерегулирование (измеряется в %) равно отношению амплитуды первого «max» отклонения регулируемой величины к установившемуся (заданному) значению

( σ max –σ зад)*100/σ зад

Качество считается удовлетворительным, если не превышает 30…40%, хорошим – превышает 20%.

5. Степень колебательности. Колебательность- число периодов переходного процесса за время регулирования. Если – 1 и 2 периода – то слабоколебательный, если больше 3х, то система требует коррекции.

6. Степень затухания (измеряется в %) – служит количественной оценкой интенсивности затухания колебательных процессов. Определяется как отношение разности первой и третьей амплитуды к первой

Ψ=(σ1-σ3)*100/σ1; удовлетворительно - 75%, допускается – 60%

7. Косвенные оценки - степень удаленности корней уравнения от мнимой оси, частотные(достаточно точные) и интегральные.

Прямой метод основан на решении дифференциальных уравнений, описывающих процессы регулирования. Способ точен и надежен, но громоздок и сложен.

Косвенные методы – приближенны, но более просты и удобны.

Типовые переходные процессы регулирования.

1. Апериодический с минимальным временем регулирования( кривая 1),отсутствие перерегулирования и минимальным регулирующим воздействием.

2. С 20 % -ным перерегулированием ( кривая 2) и минимальным временем первого полупериода колебаний, рекомендуется, когда допустима известная величина перерегулирования.

3. С минимальной квадратичной площадью регулирования ( кривая 3); характеризуется наибольшим перерегулированием (≈ 40 и 45% ) и временем регулирования; наибольшим регулирующим воздействием

- 1

- 2

-3 t

Т1

Т2

Т3

1. Процесс характеризуется минимальным временем регулирования, но имеем максимальную динамическую ошибку.

2. Меньшая динамическая ошибка, но больше время регулирования.

3. “min” динамическая ошибка и “max” время регулирования

Выбор оптимального процесса регулирования определяется видом управляемого тех. Процесса.

Оценка качества регулирования

По корням уравнения.

Передаточная функция описана дифференциальным уравнением, которое через преобразование Лапласа переводится в алгебраическое уравнение. Это уравнение можно представить в виде совокупности корней уравнения.

Показателями качества устойчивости системы является степень удаленности корней характерного уравнения, лежащих в левой комплексной полуплоскости от мнимой оси.

Jmjw Расстояние ближайшего корня от мнимой

оси характеризует запас устойчивости

η и называется степенью устойчивости

P 4-1 P2-1_ _ _ _ _ системы.

w Эта степень устойчивости определяется

действительной частью корня, ближай-

1. Re шего к мнимой оси.

P2-2 Второй показатель определяется наиболее

P4-2 удаленной мнимой частью корня от действительной оси.

Наибольший угол, образованный отрицательной действительной осью и лучом, соединяющих начало координат и значение мнимой составляющей корня, характеризует колебательность системы.

Степень колебательности( или коэффициент затухания колебаний) определяется углом, величину которого можно определить из выражения tgφ= Jm(ω)/Re(ω). Чем ближе корень располагается к мнимой оси, тем медленнее протекают переходные процессы.

Время регулирования Трег= 3Т

Для обеспечения быстроты затухания процесса нужно, чтобы все корни уравнения располагались внутри заштрихованной области.

Интегральные оценки качества.

Каждый из рассмотренных показателей качества характеризует лишь одно какое- либо свойство системы.

В основу интегральных методов положено три выражения:

Трег Трег Трег

J 1= (1/Трег) ∫ E(t)dt; J2 =(1/Трег) ∫Е²(t)dt; J3 = (1/Трег)∫ {E²(t)+ T²[dE(t)/dt]². Где

E(t) функция ошибки регулирования; Трег- время регулирования; Т- постоянная времени экспоненты, по которой желательно изменение переходного процесса.

Качество системы регулирования устанавливается по «min» интегральной оценки.

Различают линейные и квадратичные интегральные оценки.

Первый интеграл является линейной оценкой, а второй и третий - квадратичными.

Первый - определяет алгебраическую сумму площадей ограниченных кривой переходного процесса. Применим для оценки неколебательного монотонного процесса.

Качество колебательного переходного процесса лучше оценить вторым интегралом.

Д ля оценки переходных процессов с разными частотами служит третий интеграл.

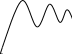
Х Х Х огибающие колебат. процесса

_ _ _ _ _ _ _ _ τ

Хо -J=∫xdt 0 - оптимальнаяt

экспонента

t t 0 t

определение площадей ограниченных оптимальный показатель

кривой переходного процесса экспоненты

Частотный метод оценки качества.

Математической основой метода является преобразование Фурье, которое позволяет получить некоторые действительные функции, называемые обобщенными частотными характеристиками.

Основное отличие между прямым и частотным методами.

Прямой - является аналитическим, требующим вычислений корней уравнений,

а частотный – графоаналитическим, не требующим вычислений корней. Исходными данными для него могут служить те же самые частотные характеристики, которые применяются при анализе устойчивости.

Частотный метод основывается на рассмотрении действительной, а не амплитудной и фазовой частотной характеристик.

Чем выше пик частотной характеристики, тем больше колебательность. Чем больше показатель колебательности, (т.е. максимум АЧХ) итем больше колебательность.

Частотный метод допускает совместное исследование качества и устойчивости систем и обладает достаточной точностью.

Интересен метод аппроксимации вещественных частотных характеристик (трапецеидальные характеристики).

Суть метода трапеций.

Используя передаточные функции объекта регулятора, записывают передаточную функцию замкнутой системы:

Заменив в формуле Лапласа Р на j ω, получают аналитическое выражение вектора АФХ. Далее по аналитическому выражению, изменяя ω от 0 до ∞, строят её график, который разбивают на несколько трапеций. Затем суммируют графики для всех трапеций. Получают график процесса регулирования.

По графику определяют показателя качества. (статическую ошибку, динамическую ошибку, время регулирования и др).

Корректирующие устройства.

Основное назначение корректирующих устройств - изменение динамических свойств системы для достижения желаемых характеристик.

Корректирующее устройство влияет на динамические свойства системы, изменяя фазовую характеристику.

Физическая основа коррекции состоит в следующем: динамические свойства меняют так, чтобы приблизить их к желаемым.

САР, состоящая только из функционально необходимых элементов, обычно не обладает требуемыми показателями качества управления. Для обеспечения заданных свойств вводят специальные корректирующие устройства.

Корректирующие устройства могут включаться либо последовательно, с основными элементами, либо параллельно или смешано.

Последовательная коррекция. Дополнительное устройство включается последовательно с элементом системы, в основном после измерительного датчика или предварительного усилителя.

В качестве последовательной коррекции используют:

Дифференцирующее (форсирующее) звено, сигнал на выходе которого содержит составляющие пропорциональные входному сигналу и производной от него.

В качестве дифференцирующих устройств могут применяться: идеальное дифференцирующее звено, инерционное дифф.звено; интегрирующее звено; интегродифф. звено.

Дифф. звенья применяются с целью обеспечения устойчивости и заданных запасов устойчивости, улучшения качества переходного процесса.

Интегр. звенья повышают точность в установленном режиме.

Параллельная коррекция.

При параллельной коррекции устройство включается параллельно или встречно- параллельно одному или нескольким основным элементам системы.

Возможна коррекция 2х видов:- прямая связь;- обратная связь.

В этом случае 2 корректирующее устройство образует местную (локальную) обратную связь. Обратная связь является эффектным средством получения требуемых динамических характеристик. На практике чаше всего используют (-) обратную связь.

В качестве 2 корр. устройств используются: усилительное звено; инерционная жесткая обратная связь; дифференц. звено; инерционная гибкая обратная связь; инерционная корректирующая обратная связь.

Дискретные системы.

Частота с которой компьютерная программа рассчитывает управляющее воздействие ( частота дискретизации или квантование времени в системе) столь велика, что ни исполнительный механизм, ни объект управления «не замечает», что изменения управляющего воздействия поступают непрерывно, а через некие малые дискретные интервалы времени. Если шаг квантования сигналов мал, то САУ практически не отличается от обычной линейной САУ.

Системы, где используется квантование времени, называются дискретными или импульсивными.

Дискретные системы бывают замкнутыми и разомкнутыми. Дискретные системы нашли применение в цифровых устройствах. Дискретизация происходит в момент, когда сигнал у(t) от объекта управления преобразуется в код.

Квантование только времени - импульсные системы.

К вантование по времени и по уровню - дискретная (цифровая) система.

X(t) Y(t)

t t

Для исследования переходных процессов и устойчивости можно применять методы, аналогичные косвенным методам исследования непрерывных систем.

Нелинейные системы.

Нелинейной называют систему, которая содержит, по крайней мере, один нелинейный элемент.

Входящие в состав САР нелинейности разделяются на существенные и несущественные, статические и динамические, однозначные и неоднозначные.

Особенности нелинейных систем.

1. Возможность существования автоколебаний

2. Для нелинейных систем неприменим принцип суперпозиции, т.е. результат суммы воздействий на САР не равен сумме результатов каждого из них в отдельности.

3. Понятие «устойчивая (не устойчивая)» нелинейная САР смысла не имеет.

4. При малых ступенчатых воздействиях переходной процесс может быть монотонным, а при больших - колебательным.

5. Не применим принцип коммутативности, что означает недопустимость перемены мест 2х последовательно соединенных элементов ( исключая звено запаздывания).

Преобразование структурных схем.

Преобразование структурных схем нелинейной системы осложняется недопустимостью суперпозиции и коммутативности.

Применяются 2 правила :

1. – перенос узла разветвления через нелинейное звено по направлению и против подачи воздействия.

2. – замена встречно - согласованного соединения эквивалентным встречно- параллельным.

Устойчивость нелинейных систем.

Д вижение выходного сигнала описывается дифференциальным уравнением nго порядка. Исследование поведения системы можно существенно упростить и сделать нагляднее, анализируя движения «n» переменных

х2 х10 х1 х2

х 10 х10 t t

- фазовые траектории интегральные кривые движения фазовых координат.

при различии нач. условиях

ПлоскостьХ1;Х2 называется фазовой плоскостью.

ф азовая плоскость , заполненная траекториями, называется фазовым портретом.

Х2 х2х2 х3 nмерное пространство

х1 х1 х1 х2

не устойч. узел не устойч. фокус седло х3

Если «n» больше «2», то рассматривают «n» - мерное пространство

Фазовые портреты удобны для оценки качественной картины движения.

Качественная картина движения целиком определяется топологической структурой фазового пространства.

Компьютеры позволяют строить реальные фазовые портреты.

Одним из характерных режимов работы нелинейной системы является автоколебательный режим, когда при отсутствии входного сигнала в системе возникают незатухающие периодические процессы.

Под линеаризацией понимают приближенную замену нелинейной функции линейной.

Если параметры автоколебаний отличаются от требуемых, то выполняют коррекцию.

Релейные (импульсные) системы автоматического управления.

Импульсное и позиционное регулирование относятся к дискретным системам управления.

Дискретные системы - у которых дискретный (прерывистый) сигнал.

Различают дискретность по уровню и по времени.

Преобразование непрерывного сигнала в дискретный называется квантованием. Примером являются релейные системы.

В дискретных системах цепь подвергается принужденному периодическому размыканию

Системы с квантованием сигнала по времени называются импульсными.

Релейное ( позиционное) регулирование – когда регулирующий орган может занимать определённое число положений ( вкл-выкл; откр-закр; больше-меньше)

Случайные воздействия.

Случайные воздействия – значения которых в момент времени неизвестны (случайные события, случайные процессы).

Статические характеристики: закон распределения; плотность вероятности; математическое ожидание; дисперсия; среднеквадратичное отклонение.

Оптимальные системы.

Оптимальной называют систему, которая обеспечивает наилучшие показатели качества. Системы, в которых заданный критерий качества обеспечивается автоматически, посредством изменения параметров или структуры, являются самонастраивающимися или адаптивными.

Экстремальные регуляторы - автоматические отыскание оптимального значения некоторого параметра.

Техническое обеспечение систем автоматического управления.

СЧПУ управляют перемещением рабочих органов станков, их скоростью при формообразовании деталей, установочными перемещениями, а также последовательностью режимов обработки и вспомогательными функциями.

Для этого используют управляющие программы. Программы содержат 2 вида информации: геометрическую и технологическую.

Геометрическая– данные о форме, размерах элементов детали и инструмента, а также об их взаимном положении в пространстве.

Технологическая - указания о последовательности ввода в работу инструментов, изменении режимов резания, смены инструментов, подачи, СОЖ и т.д.

Для преобразования сигналов при вводе и выводе из ЭВМ используют АЦП и ЦАП.

40