1. В виде произведения

jφ(ω)

W(jω)=k (ω)e , где k(ω) отношение амплитуды выходного сигнала к амплитуде входного сигнала на частоте ω.

φ(ω)- разность фаз выходного и входного сигнала на частоте ω.

Функцию к(ω) называют амплитудно- частотной характеристикой АЧХ ( является модулем); а φ(ω) – фазо- частотной характеристикой ФЧХ (является аргументом).

А(ω)=√R²(ω)+ I²(ω) – АЧХ; φ(ω) = arctgI(ω)/ R(ω). мн I(ω) - - - - - -- -

R (ω)- вещественная частотная характеристика k(ω)

I (ω) – мнимая частотная характеристика 0 φ(ω) R(ω)(веществ)

Для фиксированной частоты ω1 комплексный коэффициент передачиW( jω) может быть представлен графически в виде вектора длиной R(ω), наклонного к горизонтальной оси под углом φ(ω1)

к ак и каждое комплексное число (а +j 6) 1,2,3…..- действит.числа W( jω)

действит. мнимое ²√-1- мнимое

может быть представлено в виде суммы вещественной (действительной) и мнимой части.

W( jω)= R( ω)+ I(ω) ; R( ω)- проекция вектора W( jω) на веществ. ось

I(ω) - проекция вектора W( jω) на мнимую ось

Амплитудно- фазовые частотные функции получают заменой передаточных функций

(Р) на ( jω)

При изменении частоты ω от -∞ до+∞ конец вектораW( jω) опишет некоторую траекторию (годограф), которая называется амплитудно фазовой частотной характеристикой звена (системы) АФХ.

2. В векторной форме на комплексной плоскости

ω =∞ 0 R[W( jω)] (положительное направление фазовых

φ(ω) ω=0 R углов- против часовой стрелки)

W(jω) ω- растет [W( jω)] =k(ω)

I [W( jω)] ------------------- модуль вектора, а угол наклона -φ(ω)

сдвиг фазы выходного сигнала по отношению к входному.

е= 2,71 основание натурального логарифма

j =√-1;j²=-1 ;j³=-1√-1; jᵞ= +1

Логарифмические характеристики

АЧХ строят в двойном логарифмическом масштабе по оси абсцисс (ось х) линейно откладывают десятичный логарифм частотыω,а по оси ординат (ось у) – АЧХ, выраженную в децибелах [дб]

k(ω)[дб]= 20log10k(ω)= 20lgk(ω).

Построенную таким образом АЧХ называют ЛАЧХ (логарифмическая). При построении ЛАЧХ, по оси абсцисс удобнее откладывать логарифм безмерной величины - произведение частоты на одну из постоянных времени. ФЧХ, соответствующую ЛАЧХ, строят в полулогарифмическом масштабе, используя такую же ось абсцисс, что и для ЛАЧХ.

k (ω)(дб) φ(ω)

ωтπ/4 ωт

π/2

3/4π

π

Термины, применяемые для построения и анализе ЛАЧХ и ФЧХ, взяты из акустики. Если частоты отличаются ω2/ω1 = 2, то говорят на октаву, если ω2/ω1 =10, то – на декаду.

Изображая изменения амплитуды и частоты в логарифмическом масштабе, можно аппроксимировать (приближение) многие АЧХ прямыми или отрезками прямых.

Аппроксимация ЛАЧХ представляется прямой с наклоном 20n децибел на декаду (дб/дек), иногда (дб/откаву); 20n[ дб/дек]= 6n[ дб/дек]

Звенья первого порядка имеют наклон прямых, аппроксимирующих ЛАЧХ±20 дб/дек

Звенья второго порядка-±40 дб/дек

Звенья нулевого порядка - нулевой наклон.

Типовые элементарные звенья

Для линейных систем непрерывного действия можно назвать шесть типов элементарных звеньев; различающихся по динамическим свойствам: пропорциональное, интегрирующее, апериодическое, колебательное, дифференцирующее, запаздывающее.

1. П ропорциональное ( усилительное, безинерционное) (простое) выходная величина в каждый момент времени пропорциональна входной. Связь определяется алгебраическим уравнением: х вых= квх, где к- коэффициент усиления или передаточный.

х вх х вых х вых(t) Передает сигнал без искажения

1. ᶄ и сдвига во времени, но изменённым

t t в К раз .

Передаточная функция W(P)= х вых(Р)/х вх (Р) = К I

W(jω) с

к К

АФХ не зависит от изменения частоты ω, то годограф превращается в точку С на расстоянии к от начала координат.

Пример: манометрическая пружина, рычаг, короткий трубопровод, редуктор, электронный усилитель.

2. Интегрирующее (астатическое) (первого порядка) (нейтральное) у него скорость изменения выходной величины пропорциональна входной, а сама выходная величина пропорциональна интегралу входной.

Дифференциальное уравнение Тdхвых/ dt = хвх или Т интег=dy /dt=кx; у=к∫хdt

Операторная форма Тр х вых(Р)= хвх(Р)

Передаточная функция W(P) = х вых(Р) / х вх (Р) = 1 / ТР или = к/р

Это звено характеризуется параметрами Т и к или только ка – отношением скорости изменения выходной величины к входной.

И з передаточной функции легко получить аналитическое выражение вектора АФХ при замене оператора(Р) на выражение jω

х вх х вых х вых(t) кривая разгона

1 t0 t t0 t

I

ω =∞ R - АФХ АФХ представляет собой прямую, совпадающую с

ω2 отрицательной мнимой осью. При изменении частоты от 0 до +∞

ω3 конец вектора движется по отрицательной мнимой оси от -∞ до 0.

ω0

h (t) ᶄ(ω) -ЛАЧХ Звено обладает свойством

самовыравнивания

0 t 0 1 ωT

переходная функция L(ω)

h(t)= кt*1/(t) -20дб/дек

весовая- w(t) = к*1(t)

W (t) h(t)- переходная

к W(t) - весовая

1. t

3. Апериодическое звено (инерционное, статическое) – 1 порядка звено, в котором при скачкообразном изменении входной величины выходная величина стремится апериодически ( по закону экспоненты) к новому установившемуся значению.

Исходное дифференциальное уравнение назначается оригиналом, а преобразованное и записанное в операторной форме - его изображением.

Дифференциальное уравнение ТdХвых+ Х вых= к Х вых

dt

В операторной форме (ТР +1) х вых (Р) =к Хвх(Р) (исходное уравнение становится алгебраическим)

I

Х вх Х вых кривая разгона

Хвых(t)

ᶄ

х вх=

t0t t0 t ω

Передаточная функция W(P)= к/TP+1; P=j ω →W(j ω)= к/ T(j)+1 АФХ

действительная часть R[W(j ω)]= 1/(1+²T ω ²) ;мнимая I[w(j ω)]=-T ω /(1+T² ω ²)

А 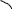ФХ имеет вид окружности, описываемой концом вектора W(jw) на комплексной плоскости при изменении wот- ∞ до+∞. При w>0 АФХ представляет полуокружность.

I ² ЛАЧХ φ(w)ФЧХ

w =∞ к АФХ h(t) переходная h() дб 3дб φ

w=0 1

-t/T функция -π/4

w1 -1-e -20 дб/дек

w2 0 t -π/2

1

Пример: сосуд с самовыравниванием, теплообменник, термопара, контуры RC;RL; электрогенератор; операционный усилитель, двигатель.

4. Колебательное звено.

Колебательным называют звено, в котором при скачкообразном изменении величины на входе выходная величина стремится к новому установившемуся значению, совершая относительно него колебания, с амплитудой, затухающей по закону экспоненты (пунктир. линии).

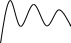х вх х вых ---I----

х вх

t0 t t0 t

Связь между входными и выходными величинами определяется дифференциальным уравнением Т1d²Хвых/dt²+ Т2dХвх/dt + Хвх=ᶄ Х вх

Операторная форма Т1Р² Х вых (Р) + Т2Р Х вых (Р) + Х вых (Р) =ᶄ Х вх (Р)

Колебательное звено имеет 3 параметра: Т0 и Т – постоянные времени, к- коэффициент усиления.

Передаточная функция W(P) = Х вых (Р)/ Х вх (Р)= к/ Т1Р²+Т2Р +1 , заменив Р→j ω

W(j ω) = к/ T1(j ω)²+T2( j ω)+1

I к Если Т2<4Т1 – то система как колебательное звено

R Если Т2≥4Т1 – то как апериодическое 2-го порядка

w 1 W(jw) Т2≥4Т1

w 3 w2 -АФХ

t

Пример: механическая система; система из двух сообщающих сосудов, мембранный сервомотор, контур RLC колёсная пара вагона.

5. Дифференцирующие звенья

Названья звеньев связано с тем, что выходной сигнал у(t) прямо пропорционален производной входного сигнала х(t) по времени

y(t)= dx(t)/dt

Различают идеальные и реальные дифференциальные звенья.

Идеальное – y=kdХвх/dt; в операторной форме Х вых (Р) = к(Р)* Х вх (Р)

Передаточная функция W(P) =Х вых (Р)/Х вх (Р) = кP

Аналитическое выражение W(j ω)= k(j ω) = 0+ jk ω; A (w) =k* ω ; φ(w)=π/2 const

Переходная функция h(t) =kd1(t)/dt= kδ(t)

I 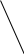m w→∞ k(w) -20дб/дек

Re 0 1 wT

годограф ЛАЧХ

П ример : электро цепь из RC C

Хвх=U1 R Х вых=U2

Реальное дифференциальное звено

Дифференциальное уравнениеТ0dХ вых/dt+ Х вых =к *dХвх/dt;

о ператорная форма То Р Х вых (Р)+ Х вых(Р)=к Р Х вх (Р

I m Хвх Х вых - Типовая кривая разгона

1

w1 tᶄ/То

w2

W=o R/To Re То

Типовая кривая разгона показывает, что после подачи на вход возмущения в виде единичного скачка выходной сигнал мгновенно увеличивается на величину к/To, а затем по экспоненте приближается к «о». По кривой разгона легко определить коэффициенты То и к передаточной функции (с помощью касательной) ( смотреть апериодическое звено)

Находят То, затем умножив ординате к/То на То, получают к.

ЛАЧХLg(ω) =20 lgk ω = 20lgk+20lg ω

L Пример: емкость, индуктивность, тахогенератор,

20lgk +20 дб/дек операционный усилитель, контурRL, контур RC.

lgw

6. Запаздывающее звено

З 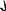вено, в котором выходная величина идеально повторяет входную, но с отставанием на постоянный отрезок времени, т.е. когда сигнал без искажения передается с задержкой во времени τ Im φ(ω)

Х вх Х вых Re 1

Rew=0 0

to t τ 1 w=1 -1

to -ФЧХ

W(j ω)=exp(-j ω t)

АЧХ k(ω) =(cos² ω t+sin² ω t)½=1

ФЧХ φ (ω)=- ω t

АФХ – окружность единичного радиуса

Пример: ленточный транспортер, транспортируемое рабочее место.

Особые звенья. Неминимально- фазовые звенья.

Связь между АЧХ и ФЧХ.

Из характеристик различных звеньев и их комбинаций видно, что существует тесная связь между АЧХ и ФЧХ.

Установив связь, можно строить ФЧХ по данной АЧХ→ и вычисление фазового сдвига становится ненужным.

Под минимальной фазой понимается минимальное фазовое запаздывание или минимальный фазовый сдвиг при заданном наклоне ЛАЧХ.

Неминимально- фазовые элементы вносят добавочное запаздывание по фазе и увеличивают возможность неустойчивости.

Фазовый сдвиг на данной частоте ωo в основном определяется наклоном АЧХ на этой частоте

φ(ω = ω o)= (π/40)d{k (ω)[дб]}/d ω [рад] ; скорость изменения АЧХ - d{k(ω)[дб]}/

d ω =±20n(дб/дек); сдвиг по фазе ±nπ/2 (радиан).

Определение неминимально-фазовых элементов.

Если элемент устойчив, т.е. знаменатель его передаточной функции не имеет корней с положительной действительной частью, то он обладает неминимально-фазовыми свойствами, если числитель его передаточной функции имеет такие корни.

Неминимально-фазовыми характеристиками обладают многие электрические цепи и многие элементы.

Например: термометр (расширительное стекло, уровень ртути падает, - только когда нагревается ртуть, он начинает расти).

Передаточные функции соединения звеньев и систем.

Виды соединений звеньев.

Любую сложную схему можно разбить на отдельные блоки с одним из трёх типовых соединений: последовательным, параллельно- согласованным или параллельно- встречным

1. Последовательное соединение звеньев.

Х

W1(P)

W2(P)

W3(P)

вх Х1 Х2 X3 Х вых

т.к. передаточная функция есть отношение, преобразованных по Лапласу, выходного сигнала звена к входному, т.к.W(P) = Х вых (Р)/ Х вх (Р); то Х вых (Р) =W(P) Х вх (Р).

Выходной сигнал каждого из звеньев в последовательной цепи можно выразить через его передаточную функцию:

Х1(Р) =W1(P)Хвх(Р); Х2(Р) = W2 (Р) Х1(Р); Хвых (Р) =Х3(Р)=W3(Р) Х2(Р)

При последовательном соединении АЧХ перемножаются, а ФЧХ- алгебраически суммируются.

W(j ω)=W1(j ω)*W2(j ω) =k1(ω)k2(ω)ej[φ(ω)+ψ(ω)]

Последовательно подставляя:

Х3 вых (Р) = W3(Р)* W2(Р) *W1(Р) * Хвх(Р) т.е. W(Р) = Хвых (Р)/ Хвх(Р)=

=W1(Р)*W2(Р)*W3(Р);

чтобы получить выходной сигнал цепи, нужно произведение передаточных функций её звеньев умножить на входной сигнал. Если использовать дифференциальное уравнение, то нужно решать каждое отдельно и получим только частное для заданных условий.

Последовательным называется соединение звеньев, при котором выходная величина предшествующего звена является входной величиной для последующего.

2. Параллельно- согласованное соединение звеньев.

Параллельным называется соединение, при котором входная величина у всех общая, а выходная – суммируется.

W1(P)

\

Х1вх Х1вых

Х

W2(P)

вх Х2вх Х2вых Х вых

W3(P)

Х3вх Х3вых

Входной сигнал обладает достаточной мощностью т.е. не уменьшается при разделении, а выходной сигнал равен сумме выходных сигналов всех звеньев.

Х вх= Х1вх=Х2вх=Х3вх

Х вых= Х1вых+Х2вых+Х3вых

Х1вых(Р)=W1 Х1вх(Р)

Х2вых(Р)=W2 Х2вх(Р)

Х3вых(Р)=W3 Х3вх(Р)

W(P)= Х вых(Р)/ Х вх(Р)=W1(Р)+W2(Р)+W3(Р)

При параллельном соединении вычисляют передаточную функцию суммы W(P)

W(P)=У(Р)/Х(Р)=W1(P)+W2(P), подставив Р=j ω → вычисляют АЧХ и ФЧХ

Передаточная функция удобна при проектировании САУ