10 Произвольная система сил. Условия и уравнения равновесия.

Произвольная плоская система сил – это система сил, линии действия которых расположены в плоскости независимо.       Любая плоская произвольная система сил, действующих на абсолютно твердое тело, при приведении к произвольно избранному центру О, может быть заменена одной силой, равняющейся главному вектору системы и приложенной в центре приведения О, и одной парой с моментом, равняющемуся главному моменту системы относительно центра О.    Уравнения равновесия – это условия равновесия, в которые входят известные активные силы и неизвестные реакции связей, т.е. аналитические условия равновесия данной системы сил.     Задача называется статически определимой, если число неизвестных реакций связей равняется числу независимых уравнений равновесия.     Если для данной конструкции число всех реакций (неизвестных) будет больше количества уравнений, в которые входят реакции, то конструкция будет статически неопределимой.      В зависимости от взаимного движения тел трение между твердыми телами бывает трех видов:

•  трение скольжения.

•  трение качения;

•  трение вращения.

• Произвольная система сил , приложенных к твердому телу, может быть заменена одной из четырех простейших систем: а) одной силой; б) системой, не содержащей сил ( нулем); в) двумя силами, образующими пару сил, и г) тремя силами, из которых две образуют пару, а третья перпендикулярна плоскости этой пары. [1]

• Произвольная система сил  в пространстве, для равновесия которой требуется выполнение установленных в § 39 шести уравнений, является общим случаем расположения сил, приложенных к телу. Выведенные нами ранее уравнения равновесия для частных случаев расположения сил можно было бы получить из данных шести уравнений, подобно тому как это было сделано выше для пространственной системы параллельных сил. [2]

• Произвольная система сил  на плоскости уравновешивается тогда и только тогда, когда выполняются два условия: 1) многоугольник сил замкнут и 2) многоугольник Вариньона замкнут. [

11 Способы задания движения точки

Прежде чем заняться исследованием движения точки, определением характеристик этого движения, надо научиться определять положение точки в пространстве в нужный момент времени.

Для этого существует несколько способов задания движения.

1. Естественный способ

Рис. 8.1

Ч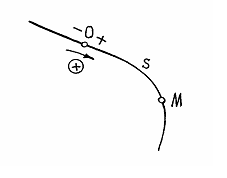 тобы определить движение точки ес­тест­вен­ным способом, должны быть заранее за­даны (рис.8.1): траектория движения точки (линия, по кото­рой точка движется); начало отсчёта (точка , от кото­рой по траектории отсчитыва­ется расстояние s до движущейся точки М); на­правление, в ко­тором от­кладываются поло­жительные зна­чения характери­стик движе­ния (указыва­ется стрелкой либо зна­ками + и −); закон движения s = s(t).

 

Пример 8.1. Точка движется по прямой линии, по закону   (рис. 8.2).

В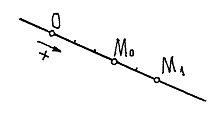 начале движения, при ,   Положение точки  назы­вается  начальным положением.   При  

Рис. 8.2

Конечно, за  точка прошла расстоя­ние M₀M₁=2 см. Так что s – это не путь, пройденный точ­кой, а расстояние от начала отсчёта до точки.

2. Координатный способ

Этим способом положение точки в какой-либо системе координат определяется её координатами  (рис. 8.3).  При движении точки эти  координаты изменяются. Поэтому, чтобы определить положение точки в нужный момент времени, должны быть заданы координаты как функции времени :                            

.

Эти функции называются уравнениями движения точки.

Уравнения движения позволяют определить не только положение точки в любой момент времени, но и все характеристики движения, в том числе и траекторию движения.

Чтобы получить уравнение траектории, надо из уравнений движения исключить параметр .

 Пример 8.2. Движение точки задано уравнениями (x, y – в см, t – сек):

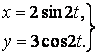
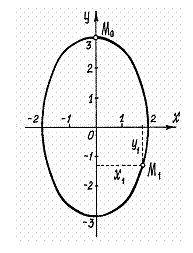
Чтобы исключить время, параметр t, найдём из первого уравнения  из второго  Затем возведём их в квадрат и сложим. Так как  получим  Это уравнение  эллипса  с полуосями  и  (рис. 8.4).

Н ачальное  положение  точки   (при )    определяется  координатами          Через   точка  будет  в положении    с координатами  

Примечание

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости с заданием движения цилиндрическими и сферическими координатами можно ознакомиться по учебникам.

3. Векторный способ

Положение точки можно определить заданием вектора , проведённого из неподвижной точки , предполагая, что точка  находится на конце этого вектора (рис. 8.3). Этот вектор называется радиусом-вектором точки M. Конечно, чтобы определить положение точки в любой момент времени, радиус-вектор должен быть задан как функция времени  

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор  на составляющие по осям координат:

  где  – проекции вектора на оси; – единичные векторы, направленные по осям, орты осей. Так как начало  вектора находится в начале координат, то проекции вектора будут равны координатам точки  M.  Поэтому

                                             (8.1)

  Траектория движения точки  – это линия, которую описывает ко- нец изменяющегося радиуса-вектора. Эта линия называется  годографом        вектора .