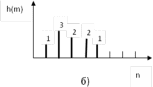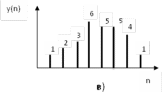- •Мазмұны
- •Комплексті X(z) функциясы (1) дәрежелік қатары үйлесетін барлық z үшін қолданылады.
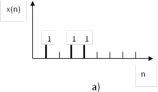
- •1 Сурет – Цифрлық фильтр: а) кіріс сигнал; б) импульстік сипаттама;
- •2 Сурет - Рекурсивті емес сүзгінің сұлбасы
- •Есеп № 2
- •3 Сурет - Тура түрдегі рекурсивті сүзгінің құрылымдық сұлбасы
- •4 Сурет - Канондық түрдегі рекурсивті сүзгінің құрылымдық сұлбасы
- •5 Сурет – Транспонирленген түрдегі рекурсивті цифрлы сүзгінің жалпы түрдегі құрылымдық сұлбасы
- •Қорытынды
- •Қолданылған әдебиеттер тізімі
Мазмұны
Кіріспе..................................................................................................................... |
3 |
Есеп №1.................................................................................................................. |
4 |
Есеп №2.................................................................................................................. |
9 |
Қорытынды............................................................................................................. |
13 |
Қолданған әдебиеттер тізімі................................................................................. |
14 |
Кіріспе
Аналогты жүйелердің сызықты анализі мен синтезі уақыттық облыстан жиіліктік облысқа көшкен кезде біршама ыңғайланады. Лаплас түрлендіруі бірінші ретті рационалды анализі үшін ыңғайлы іргетастық түсінік беріліс функциясын енгізуге мүмкіндік берді. Сондай-ақ кіріс-шығыс қатынасын жай алгебралық теңдеулермен жазуға болатын болды. Сол сияқты дискретті жүйелерді сызықтық анализі мен синтезі уақыттық облыстан Z-облысына көшкенде біршама ыңғайланады. Атап айтқанда Z-түрлендіруі бөлшекті рационалдық түрге берілу функциясын беруге мүмкіндік беріп, кіріс-шығыс қатынасын әртүрлілік теңдеулермен емес, жай алгебралық теңдеулермен жазуға болатын болды.
Z-түрлендіруі x(nТ)-дискретті тізбегін, оның Z бейнесі Х(Z)-пен бір мәнділікпен байланыстырады және ол мына қатардың абсолютті жинақтау облысында ғана орындалады. Оны Z-бейнесінің жинақталу облысы деп атайды.
Аналогты сигналдарға Лаплас түрлендіруін қолданғанымыз сияқты, дискретті x(n) - сигандың тізбектерін, оның белгілі болған Z-бейнесі Х(Z)-арқылы табу үшін кері Z-түрлендіруін қолдануға болады.
Z-түрлендіруінің 5 қасиеті бар, олар: сызықтылық қасиеті, кідіріс қасиеті, белгілі дәрежелі шамаға көбейту қасиеті, n-ға көбейту қасиеті, үйірткі қасиеті.
Есеп №1
а) Келтірілген {x(n)}={1,0,1,1,0,0…}; {h(m)}={1,3,2,2,1} цифрлық функцияның z-түрлендіруін алу қажет ;
б)
Келтірілген Х(Z)= функцияның қайта z-түрлендіруін алу
қажет.
функцияның қайта z-түрлендіруін алу
қажет.
№1 Есептің шешуі:
Тура Z-түрлендіру
x(n) функциясының – нақты немесе комплексті санаулар тізбегінің тура Z-түрлендіруі деп келесі өрнекті айтады:
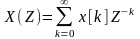 (1)
(1)
Біздің
жағдай үшін: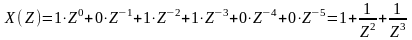
Комплексті X(z) функциясы (1) дәрежелік қатары үйлесетін барлық z үшін қолданылады.
X(n) спектрлік коэффициенттері, яғни {z(n)} тізбегінің, {n=0,1,…,N-1}, ДФТ – сі осы тізбектің Z – түрлендіруінің бірлік шеңберде орналасқан бір қалыпты орналасқан N нүктелеріндегі мәндеріне тең.
1.2 Жүйенің берілген импульстік сипаттамасы арқылы {y(n)} дискретті үйіртіні анықтау. Жүйелік функцияны табу:
Дискретті тізбектің шығысындағы сигнал тізбектің кірісіндегі тізбекпен дискретті үйірткінің формуласы арқылы байланысты, сондықтан дискретті шығыс тізбегінің n-ші санауы келесі формула көмегімен есептелінеді:
|
(2)
|
Кесте - Дискретті үйірткі {y(n)}
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
0 |
2 |
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
2 |
2 |
0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
0 |
3 |
2 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
3 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||
y(0)=1·1=1; y(1)=1·2+0·1=2; y(2)=1·2+0·2+1·1=3
y(3)=1·3+0·2+1·2+1·1=6; y(4)=1·1+0·3+1·2+1·2+0·1=5; y(5)= 0·1+1·3+1·2+0·2+0·1=5
y(6)=1·1+1·3+0·2+0·2=4; y(7)=1·1+0·3+0·2=1; y(8)= 0·1+0·3=0
y(9)= 0·1=0
{y(n)}={1,2,3,6,5,5,4,1,0,0}
Соңғы өрнектен тізбектің һ(т) импульстік сипаттамасының Z-түрлендіруі дискретті тізбектің H(z) беріліс сипаттамасы болып табылатынын көруге болады.