
- •Contents
- •Введение
- •«Горячие точки» ии (д.А. Поспелов, г.С. Осипов)
- •Основные этапы развития ис (эс)
- •Классификация эс как приложений
- •Методы обработки плохоопределенной информации в ис (эс)
- •Теоретико-вероятностные методы оперирования с неопределенностью
- •Байесовские сети доверия (Bayesianbeliefnetworks)
- •Метод субъективных коэффициентов уверенности (субъективных вероятностей)
- •Теория свидетельств Демпстера-Шефера
- •Правило объединения свидетельств
- •Вероятностная логика
- •Поиск решения в условиях неопределенности с использованием деревьев решения (др)
- •Методы обработки неопределенности вGuru
- •Использование нечетких переменных
- •Обработка неопределенности лингвистического характера
- •Конструирование эс (соз)
- •Структура современных инструментальных средств для разработки эс
- •Классификация инструментальных средств конструирования эс
- •Тенденции развития инструментальных средств конструирования эс
- •Приобретение знаний
- •Средства приобретения знаний
- •Методы психосемантики
Метод субъективных коэффициентов уверенности (субъективных вероятностей)
MYCIN
Mд(H,E)
=



Доверие (гипотеза, мера)
Mн(H,E)
=
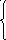

Недоверие
K(H,E) = Мд(Н,Е) – Мн(Н,Е)
Мн 1,
Мд
1,
Мд 0
0
-1

P(R)=0.5P(R|Z)=0.75
Мд
=
 = 0.5
= 0.5
Мн=
 = 0
= 0
K(R,Z) = 0.5 – 0 = 0.5
Можно ввести Kверхпорог(H,E) = 0.2
Kнижпорог(H,E) – не зависит от ситуации
Сложное свидетельство – есть ряд свидетельств, которые используются для гипотезы.
Если Е1и Е2независимы, то:

Мд(H,E1&E2) =


Мн(H,E1&E2) =

Сложная гипотеза – свидетельство в поддержку всех гипотез
Мд(H1&H2,E) =min{ Мд (H1,E), Мд (H2,E)}
Мн(H1&H2,E) =max{ Мн (H1,E), Мн (H2,E)}
Мд(H1&H2,E) =max{ Мд (H1,E), Мд (H2,E)}
Мн(H1&H2,E) =min{ Мн (H1,E), Мн (H2,E)}
Мд(Ht&Hq,Ei&Ej) =min{ Мд (Ht,Ei&Ej), Мд (Hq,Ei&Ej)}


по (1)
Мн(Ht&Hq,Ei&Ej) =max{ Мн (Ht,Ei&Ej), Мн (Hq,Ei&Ej)}


по (2)
Если сами свидетельства правдоподобны, то надо перейти на метод шкалирования.

-а 0 +а
Мд(H,E) = Мд (H,E) max{
К(E,А); 0}
max{
К(E,А); 0}
Мн(H,E) = Мн (H,E) max{
К(E,А); 0}
max{
К(E,А); 0}
Теория свидетельств Демпстера-Шефера
Схема Байеса основывается на:
Р(Н)+Р(⌐Н)=1 – свойство дополнительности
Свойство индифферентности
Точечная оценка
Аксиоматика ТВ по Колмогорову:
0
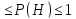
P(true)=1, P(false)=0
P(HvQ) = P(H)+P(Q)-P(H&Q) => P(Hv⌐H)=1
Базовые посылки ТС:
Использование субъективных свидетельств
Различение ситуаций неопределенности и незнания
Использование правила объединения свидетельств
1967г
[Р+(Н), Р+(Н)] – вероятностный интервал доверия
Шефер ввел понятия меры (функции) доверия гипотезы Н (Bel(H)) и меры правдоподобияPl(H)=1 -Bel(⌐H). Вероятностный интервал доверия – [Bel(H),Pl(H)]
 –множество
всех возможных подмножеств из {H}
гипотез.
–множество
всех возможных подмножеств из {H}
гипотез.
Задается
базовое распределение вероятностей
(мера m(Нi))
на множестве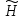 :
:

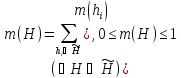
Функция (мера) доверия к гипотезе Н:
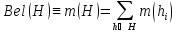
Мера недоверия (правдоподобия) к гипотезе Н:

Пример
Вы миллионер и думаете, покупать ли фирму.
1) пригласили эксперта А
Р(Ав)=0,9 Р(Ан)=0,1
h – покупать акции
Bel(h)=0,9 Pl(h)=1- Bel(⌐h)=1
Вероятностный интервал доверия – [0.9; 1]
2)пригласили эксперта Б
Р(Бв)=0,8 Р(Бн)=0,2
Эксперт Б говорит h.
Нужно посчитать:
Р(Ав&Бв)
= Р(Ав) Р(Бв)
= 0,9
Р(Бв)
= 0,9 0,8
= 0,72
0,8
= 0,72
Р(Ан&Бн)
= Р(Ан) Р(Бн)
= 0,1
Р(Бн)
= 0,1 0,2
= 0,02
0,2
= 0,02
Р(Ав vБв) = 1 - Р(Ав&Бв) = 1 – 0,02 = 0,98
Bel(h)=0,98 Pl(h)=1- Bel(⌐h)=1
Вероятностный интервал доверия – [0.98; 1]
А → h, Б → ⌐h
Р(Ав&Бн)
= Р(Ав) Р(Бн)
= 0,9
Р(Бн)
= 0,9 0,2
= 0,18
0,2
= 0,18
Р(Ан&Бв)
= Р(Ан) Р(Бв)
= 0,1
Р(Бв)
= 0,1 0,8
= 0,08
0,8
= 0,08
Р(Ан&Бн)
= Р(Ан) Р(Бн)
= 0,1
Р(Бн)
= 0,1 0,2
= 0,02
0,2
= 0,02
Р(Ав vБв) = 1 - Р(Ав&Бв) = 0,18 + 0,08 + 0,02 = 0,28

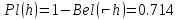

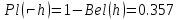
Вероятностный интервал доверия h– [0.643; 0.714]
Вероятностный интервал доверия ⌐h– [0.286; 0.357]
Р(Aв)=0,9Р(Бв)=0,9
А → h, Б → h
Вероятностный интервал доверия h– [0.99; 1]
А → h, Б → ⌐h
Вероятностный интервал доверия h– [0.47; 0.53]
Вероятностный интервал доверия ⌐h– [0.47; 0.53]
Правило объединения свидетельств
 –образует
всевозможные подмножества взаимоисключающих
гипотез.
–образует
всевозможные подмножества взаимоисключающих
гипотез.
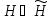

mn(H) – мера доверия к гипотезе Н, аn– число источников свидетеств.
 (*)
(*)
Пример
4 гипотезы: пациент – h1 – в шоке,h2 – грипп,h3 – мигрень,h4 – минингит
Свидетельство 1: у пациента лихорадка
m1({h1,h2,h4})=0.6
m1( )=0.4
)=0.4
Свидетельство 2: у пациента рвота
m2({h1,h2,h3})=0.7
m2( )=0.3
)=0.3
|
m1 |
m2 |
m3 |
|
m1({h1,h2,h4})=0.6 |
m2({h1,h2,h3})=0.7 |
m3({h1,h2})=0.42 |
|
m1( |
m2({h1,h2,h3})=0.7 |
m3({h1,h2,h3})=0.28 |
|
m1({h1,h2,h4})=0.6 |
m2( |
m3({h1,h2,h4})=0.18 |
|
m1( |
m2( |
m3( |
Вывод:
Высокая мера доверия
 свидетельствует о конфликте свидетельств
на множестве
свидетельствует о конфликте свидетельств
на множествеПри наличии большого множества гипотез и сложности свидетельств метод хотя и может привести к большим и сложным вычислениям, но их все же меньше, чем для Байесовской схемы.
Подход Демпстера-Шефера, основанный на свидетельствах, во многих приложениях позволяет более адекватно учитывать неопределенность, чем строгий Байесовский подход.

 )=0.4
)=0.4 )=0.3
)=0.3 )=0.4
)=0.4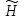 )=0.3
)=0.3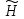 )=0.12
)=0.12