3. Переходные процессы в контуре с последовательным соединением резистивного, индуктивного и емкостного элементов

3.1 Дифференциальное и характеристическое уравнения

Пусть электрическая цепь рисунка 3.1 включена на постоянное напряжение . В момент напряжение . В момент ключ переводят из положения 1 в положение 2, при этом образуется

н акоротко замкнутый контур rLC, в котором до коммутации конденсатор был заряжен до напряжения . После коммутации в этом замкнутом контуре rLC протекает свободный процесс, который в соответствии со вторым законом Кирхгофа, описывается однородным уравнением

.

Так как , то

. (3.1)

Этому дифференциальному уравнению второго порядка соответствует характеристическое уравнение , или

(3.2)

и два корня . (3.3)

Введем обозначения:

- коэффициент затухания;

- резонансная частота.

Тогда уравнение (3.2) примет вид и его корни

. (3.4)

3.2 Апериодический разряд конденсатора

Свободный процесс, наблюдаемый в замкнутом rLC – контуре после коммутации, представляет собой апериодическую разрядку конденсатора, когда докоммутационное напряжение на конденсаторе постепенно спадает до нуля. С энергетической точки это означает, что при разрядке конденсатора, откладываемая им энергия идет на нагревание резистивного элемента и малая часть переходит в энергию магнитного поля индуктивного элемента и далее энергия, которая запасалась в магнитном поле индуктивности, переходит в тепло.

Апериодический процесс разрядки конденсатора имеет место, если корни характеристического уравнения вещественны, различные и всегда должны быть отрицательны, то есть если в уравнении (3.3) будет следующее неравенство

или .

Сопротивление называется критическим, так как оно является наименьшим сопротивлением rLC – контура, когда еще имеет место апериодический процесс разрядки конденсатора.

Таким образом, если корни характеристического уравнения и будут вещественными и различными ( ), то общее решение однородного дифференциального уравнения (3.1) имеет вид

, (3.5)

где и – постоянные интегрирования;

и – показатели затухания, которые должны быть отрицательными, так как свободный процесс должен быть затухающим во времени.

Электрический ток в накоротко замкнутом rLC – контуре будет свободным

. (3.6)

Подставляя начальные условия (при и ) в (3.5) и (3.6) получаем

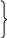
(3.7)

Имеем два уравнения с неизвестными и . Считая , раскрываем главный определитель и записываем неизвестные

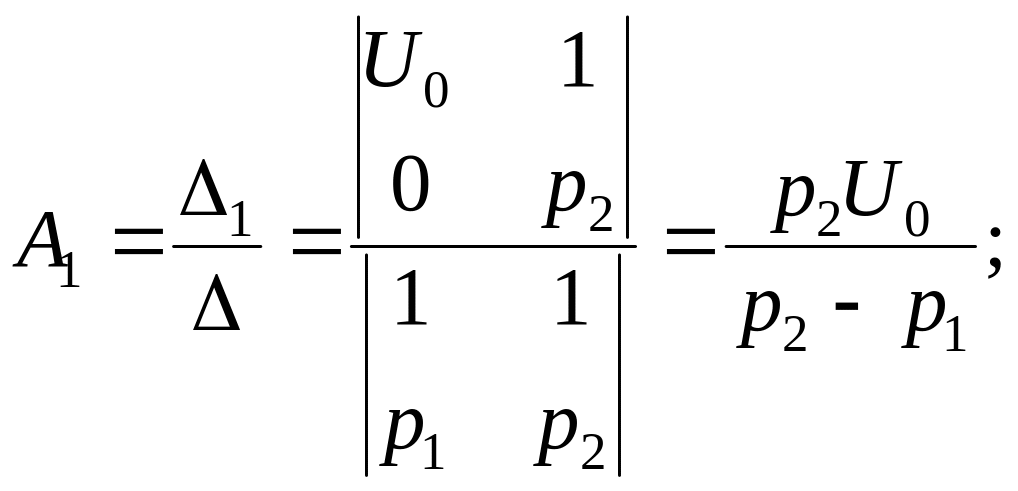
(3.8)

П одставляя эти значения в уравнения (3.5) и (3.6), окончательно получим

(3.9)

Так как производные корней и характеристического уравнения согласно теоремы Виета равно свободному члену , то для тока получим

(3.10)

Напряжение на индуктивном элементе определяется по формуле

(3.11)

Кривые изменения напряжения на емкости и на индуктивности показаны на рисунке 3.2. Кривая тока (рис. 3.2,б) находится в отрицательной области, так как происходит апериодическая разрядка конденсатора. Так как ток , то максимум кривой тока и точка перегиба кривой напряжения имеют место в один и тот же момент времени (рис. 3.2,а,б), а кривая в этот м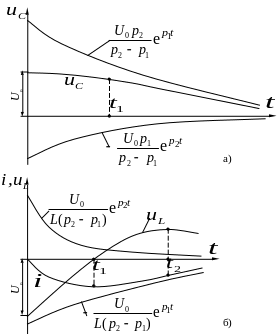 омент времени меняет знак, что следует из соотношения .

Рис. 3.2

Напряжение на индуктивности возникает скачком, в начальный момент ( ) , затем уменьшается по абсолютному значению, проходит через нуль при равенстве экспонент и, став положительным, возрастает до максимального значения (при ), после которого уменьшается и стремится к нулю.

Увеличение индуктивности приводит к уменьшению абсолютных значений корней характеристического уравнения и к замедлению возрастания тока и спада напряжения на емкостном

элементе .