2.3 Переходной процесс в катушке индуктивности при подключении ее к источнику синусоидального напряжения

Докоммутационный режим (цепь разомкнута рис. 2.3,а). Послекоммутационный режим ,

где и .

Входное сопротивление цепи . Характеристическое уравнение , откуда корень .

Выражение свободной составляющей тока . Постоянная интегрирования определяется для времени из уравнения

,

где по закону коммутации

;

;

.

Тогда выражение преобразуется к виду

Откуда .

0

а)

Рис.2.3

u

u

u

К

R

L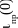

б)

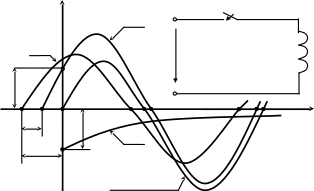
Характер изменения тока переходного процесса при подключении реальной катушки индуктивности к источнику синусоидального напряжения будет описываться уравнением

(2.8)

Этому уравнению соответствует график изменения тока переходного процесса, представленного на рисунке 2.3,б (приведены зависимости , , и .

Из уравнения (2.8) видно, что при переходной ток равен нулю, а начальное значение свободного тока равно и противоположно по направлению принужденному току . Максимальное начальное значение свободного тока будет в тот момент, когда , так как в этот момент (рис.2.4).

u

u

Рис. 2.4

Из графика рисунка 2.4 видно, что переходной ток – цепи при ее включении нарастает от нуля и в некоторые промежутки времени может превосходить максимальное значение установившегося тока, то есть может возникнуть сверхток. Однако, наибольшее значение переходного тока не превышает двойной амплитуды установившегося тока.

Следует иметь в виду, что сверхтоки, возникающие при коммутации в электрических цепях, весьма опасны из-за повышающихся динамических усилий между токонесущими элементами и вызывают перенапряжения на участках цепи, что может привести к выходу из строя аппаратуры.

2.4 Переходной процесс в конденсаторе при подключении его к источнику постоянного напряжения через резистор

При включении – цепи на постоянное напряжение (рис. 2.5,а) конденсатор будет заряжаться до принужденного напряжения . Докоммутационный режим характеризуется тем, что , и .

П

u_Спр

u_С

u_С=u_Cпр+u_Ссв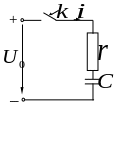

ослекоммутационный режим .

u_Ссв

t

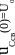
б)

а)

Рис. 2.5

Входное сопротивление цепи , характеристическое уравнение будет , откуда .

Постоянная интегрирования определяется из уравнения для то

тока при

Применяя второй закон Кирхгофа для послекоммутационной схемы (ключ k замкнут) при имеем .

Воспользовавшись вторым законом коммутации

.

Поэтому ; ;

Отсюда постоянная интегрирования .

Окончательное выражение тока переходного процесса будет

(2.9)

где - постоянная времени цепи.

Характер изменения напряжения на зажимах конденсатора определяется из уравнения второго закона Кирхгофа .

Откуда

; (2.10)

где ; .

Уравнениям переходных значений тока (2.9) и напряжения (2.10) соответствуют графики, изображенные на рисунке2.5,б.