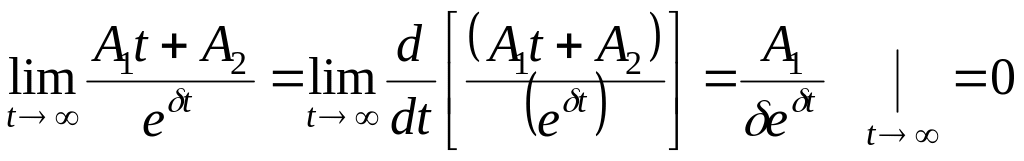1. Составление характеристического уравнение

Анализ переходных процессов в разветвленных электрических цепях классическим методом сводится к составлению системы независимых интегрально – дифференциальных уравнений по законам Кирхгофа для мгновенных значений напряжений и токов отдельных ветвей и решению этой системы относительно одного из искомых токов или напряжений.

В результате получается линейное неоднородное интегрально – дифференциальное уравнение с постоянными коэффициентами, решение которого находится в виде суммы принужденной и свободной составляющих.

Составление характеристического

уравнения методом алгебраизации

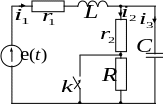
Пусть в цепи, представленной на рисунке 1.1, переходной процесс вызван скачкообразным изменением одного из параметров цепи. Составить характеристическое уравнение электрической цепи.

Электрическое состояние цепи в послекоммутационной схеме описывается системой уравнений

;

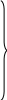(1.15)

;

.

Рис. 1.1

Решение системы линейных неоднородных дифференциальных уравнений (1.15) производится в два этапа. На первом этапе находятся значения напряжений и токов принужденного режима, а на втором этапе определяются значения составляющих свободного режима.

Индексы токов в уравнениях дополняются индексом св , а э.д.с. или напряжения источников питания приравниваются к нулю. Система уравнений для свободных составляющих имеют вид

;

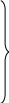; (1.16)

.

Воспользовавшись выражениями (1.7), система (1.16) алгебраизируется и приводится к виду для составления определителя

;

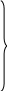
; (1.17)

.

Определитель получившейся системы (1.17) алгебраических уравнений запишется как

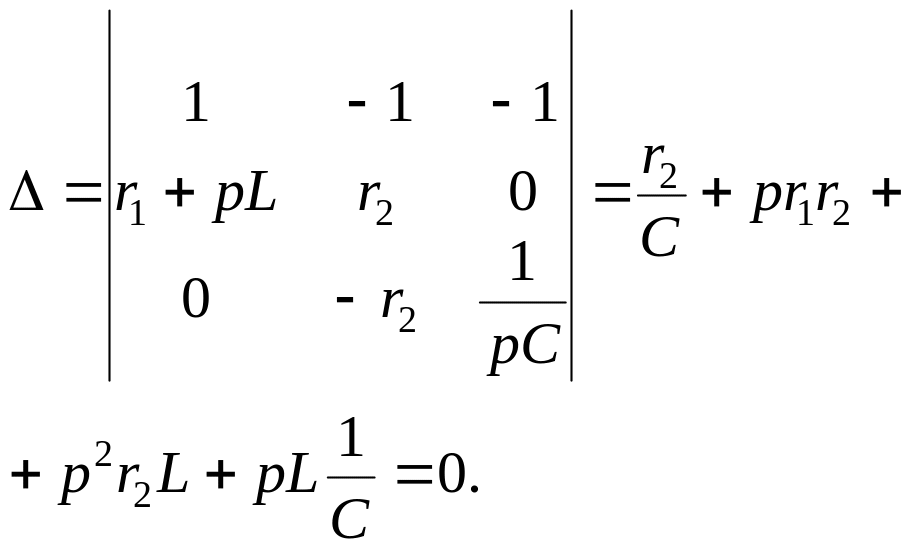
Уравнение является характеристическим, умножив последнее на С будем иметь

;

и

(1.18)

ли

.

Решая уравнение (1.18), найдем показатель затухания (корни характеристического уравнения).

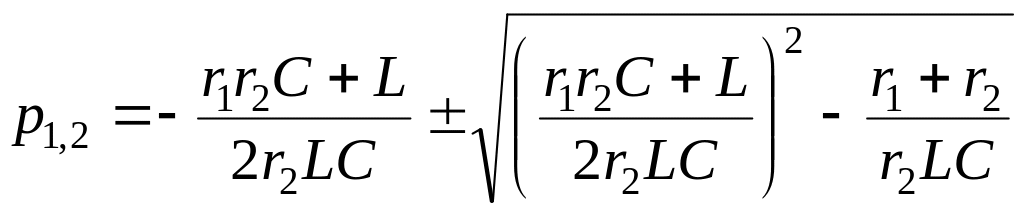. (1.19)

Составление характеристического уравнения с использованием комплекса входного сопротивления

Выражение характеристического уравнения составляется значительно проще с использованием комплекса входного сопротивления относительно зажимов любой из ветвей электрической цепи.

Для электрической цепи, изображенной на рисунке 1.1, выражение входного сопротивления относительно зажимов запишется как

.

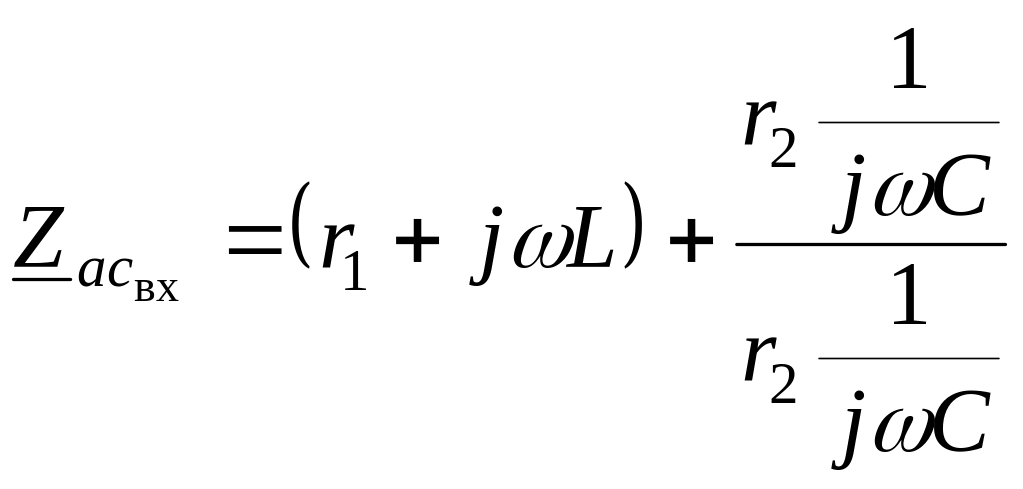Заменив на и приравняв , получим характеристическое уравнение

.

После элементарных алгебраических преобразований характеристическое уравнение примет вид аналогично уравнению (1.18).

.

2. Характер протекания свободного режима

Как было уже показано выше, составляющие искомого параметра свободного режима следует искать в виде

.

Число слагаемых функций равно числу корней , а следовательно степени характеристического уравнения.

Корни характеристического уравнения зависят только от схемы послекоммутационной цепи и ее параметров. Они определяют характер и длительность свободного режима.

Пусть характеристическое уравнение цепи будет первой степени, тогда корень такого уравнения будет действительным и отрицательным, то есть . Составляющая свободного режима для любого искомого параметра (тока, напряжения)

.

Это уравнение показывает, что с течением времени свободная составляющая затухает по показательному закону. Теоретически стремится к нулю при времени , стремящемуся к бесконечности. Практически свободный режим заканчивается очень быстро, за доли секунды.

Для оценки длительности протекания свободного режима, а следовательно, и переходного процесса вводится величина, называем

называемая постоянной времени цепи и равная .

Из последнего выражения легко убедиться, что за промежуток времени, отсчитанный с момента коммутации и равный постоянной времени, цепи , свободная составляющая по абсолютному значению уменьшается в раз по отношению к своему начальному значению. За промежуток времени свободная составляющая затухает в раз, за время - в раз и так далее.

Таким образом, за каждый новый промежуток времени, равный , абсолютное значение свободной составляющей уменьшается в раз. Данные о затухании во времени свободной составляющей относительно ее начального значения приведены в таблице 1

Таблица 1

Время с момента коммутации	0	0,2	0,4	0,6	0,8	1,0	1,5	2	3	4	5
	А	0,819А	0,67А	0,549А	0,45А	0,368А	0,223А	0,135А	0,05А	0,018А	0,007А

Из таблицы 1 видно, что переходный процесс в цепи заканчивается за промежуток времени равный .

Постоянную времени можно получить опытным путем из осциллограммы кривой свободной составляющей. Для этого к кривой (рис. 1.2) в любой её точке проводят касательную.

Длина подкасательной CD в принятом масштабе времени численно равна постоянной времени цепи. Действительно,

если учесть, что , производная , то действительно .

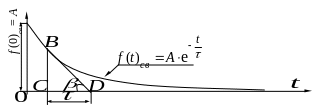
Рис. 1.2

Теперь рассмотрим характер протекания свободного режима в цепи, для которой характеристическое уравнение имеет вторую степень.

Корни характеристического уравнения второй степени (1.19) можно записать как

, (1.20)

где C и D - положительные постоянные, зависящие от соотношения параметров пассивных элементов цепи и схемы их соединения.

В зависимости от значений постоянных C и D возможны характерные случаи:

1. Если , то получается два действительных рррррррр

неравных и отрицательных корня

, ,

.

Для рассматриваемого случая выражения свободных составляющих токов и напряжений

. (1.21)

Составляющая свободного режима состоит из алгебраической суммы двух затухающих по экспоненциальному закону функций времени. Длительность и характер свободного режима зависит от значений постоянных времени цепи для каждой экспоненциальной функции в отдельности

, .

Т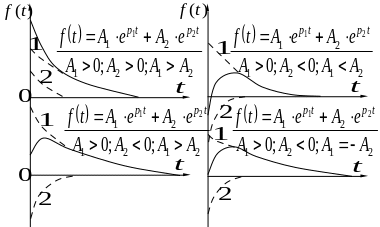 ак как и , то функция будет затухать быстрее функции .

Рис. 1.3

Характер изменения составляющих свободного режима при различных по величине и знаку постоянных интегрирования и показаны на рисунке 1.3. На графиках свободная составляющая представлена сплошной кривой, полученной путем суммирования ординат кривых первой и второй и носит апериодический характер.

2. Если имеет место условие, когда , то в этом случае корни характеристического уравнения получаются комплексные и сопряженные с отрицательной действительной частью.

Выражения для корней имеют вид

;

(1.22)

Обозначив и , получим

; ;

Выражение составляющих свободного режима будет иметь вид

(1.24)

Из этого выражения видно, что составляющая свободного режима состоит из двух гармонических колебаний с частотой .

Амплитуды и затухают во времени по экспоненциальному закону.

В ыражение гармонического колебания (1.24) можно представить проекцией синусоиды и косинусоиды на ось ординат вращающихся двух векторов и с угловой частотой (рис. 1.4).

И звестно, что сумма проекций двух векторов на ось ординат равна проекции суммы этих векторов и амплитуда общего гармонического колебания будет

, а начальная фаза .

Окончательное выражение свободных составляющих запишется в виде общего гармонического колебания

. (1.25)

График функции показан на рисунке 1.5.

Таким образом, свободный режим и переходной процесс имеет колебательный характер.

Длительность этого процесса определяется постоянной времени . Следует иметь в виду, что колебательный характер протекания свободного режима возможен только при наличии в послекоммутационной цепи индуктивности и емкости.

3.Если имеем , то при этом условии существуют два одинаковых корня .

Рис. 1.5

Выражение для составляющих свободного режима получим из выражения (1.24).

Для этого найдем предел сближения корней и к их общему значению. При сближении корней стремится к нулю, а к единице. Раскроем неопределенность вида , в которую обращается первое слагаемое уравнения (1.24).

При - стремящимся к нулю, . После сокращения получим выражение для составляющей свободного режима

. (1.26)

Свободная составляющая (1.26) при стремится к нулю. В этом легко убедиться, если по правилу Лопиталя раскрыть неопределенность