9 Методические указания к выполнению курсовой работы
К представленным на проверку курсовым работам (КР) предъявляются следующие требования:
Курсовая работа выполняется в виде пояснительной записки (ПЗ) объёмом 20-30 стр., на одной стороне листа писчей бумаги формата А4 (297
210
мм) с рамкой по ГОСТ 2.301 с основной
надписью по форме 2-для первых листов
глав и по форме 2а-для последующих листов
по ГОСТ 2.104.Структура ПЗ: титульный лист с номером варианта, реферат, содержание ПЗ, введение, основная часть, выводы и предложения, список используемой литературы, приложения.
Рисунки, графики, электрические схемы, в том числе и заданные условием задачи, должны быть выполнены аккуратно и в удобочитаемом масштабе.
Иллюстрации следует располагать так, чтобы их было удобно рассматривать и обозначаются словом «Рис.» с нумерацией в пределах раздела и подрисуночной надписью.
Оформление таблиц ПЗ осуществлять в соответствие [9].
Требования к оформлению списка использованной литературы выполнять по ГОСТ 7.1-84.
Основные примеры библиографических описаний приведены [8].
Работа над курсовой работой помогает студентам проверить степень усвоения ими раздела курса ТОЭ, вырабатывает у них навык четко и кратко излагать свои мысли. Для успешного достижения этой цели необходимо руководствоваться следующими правилами:
начиная выполнять курсовую работу по анализу переходных процессов в линейных электрических цепях указать, какие расчетные методы и законы предполагается использовать, привести математическую запись этих законов и методов с их пояснением;
используемые буквенные или цифровые обозначения в курсовой работе подлежат пояснению значения каждого обозначения;
в ходе выполнения КР не следует изменять однажды принятые направления токов и наименования узлов, сопротивлений, а также обозначения, заданные условием;
расчет каждой определяемой величины следует выполнять сначала в общем виде, а затем в полученную формулу подставить числовые значения и привести окончательный результат с указанием единиц измерения. Промежуточные и конечные результаты расчетов должны быть ясно выделены из общего текста;
при построении кривых следует выбирать такой масштаб, чтобы кривая переходного процесса имела наглядность. Градуировку осей выполнять в масштабе, начиная с нуля. Весь график в целом и отдельные кривые на нём должны иметь названия.
ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ
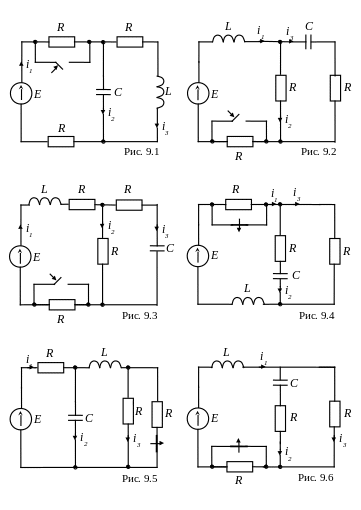
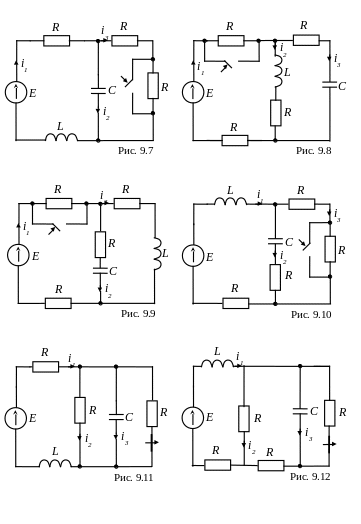
В электрической цепи (рис.9.1-9.24) происходит коммутация. В цепи действует постоянная э.д.с, параметры цепи и э.д.с. для задач приведены в таблицах 9.1 и 9.2. Требуется определить закон изменения тока во времени в ветвях цепи или напряжение на каком-либо элементе при переходном процессе в цепи второго порядка.
Задачи следует
решать двумя методами: классическим и
операторным. На основании полученного
аналитического выражения требуется
построить графики изменения искомой
величины в функции времени в интервале
от
до
,
где
- меньший по модулю корень характеристического
уравнения.
Номер варианта |
Номер рисун-ка |
E, B |
Таблица 9.1 |
|||
R, Ом |
L, Гн |
С, мкф |
Определить |
|||
1 |
9.1 |
100 |
100 |
1,3 |
20 |
i1,i2,i3 |
2 |
9.2 |
250 |
100 |
0,9 |
10 |
i1,i2,i3 |
3 |
9.3 |
160 |
40 |
1 |
40 |
i1,i2,i3 |
4 |
9.4 |
80 |
50 |
1,2 |
30 |
UL |
5 |
9.5 |
60 |
50 |
1,3 |
80 |
UC |
6 |
9.6 |
150 |
60 |
0,8 |
20 |
UR |
7 |
9.7 |
90 |
70 |
0,6 |
20 |
i1,i2,i3 |
8 |
9.8 |
120 |
70 |
0,5 |
10 |
i1,i2,i3 |
9 |
9.9 |
180 |
80 |
0,2 |
90 |
i1,i2,i3 |
10 |
9.10 |
50 |
90 |
1 |
150 |
UL |
11 |
9.11 |
90 |
60 |
0,9 |
40 |
UC |
12 |
9.12 |
240 |
100 |
0,4 |
60 |
UR |
13 |
9.13 |
130 |
50 |
1,25 |
80 |
i1,i2,i3 |
14 |
9.14 |
140 |
110 |
0,5 |
70 |
i1,i2,i3 |
15 |
9.15 |
80 |
60 |
1,3 |
50 |
i1,i2,i3 |
16 |
9.16 |
50 |
70 |
1,25 |
40 |
UL |
17 |
9.17 |
140 |
90 |
0,9 |
20 |
UC |
18 |
9.18 |
160 |
110 |
0,9 |
10 |
UR |
19 |
9.19 |
180 |
50 |
0,07 |
55 |
i1,i2,i3 |
20 |
9.20 |
70 |
70 |
0,6 |
20 |
i1,i2,i3 |
21 |
9.21 |
50 |
120 |
0,6 |
80 |
i1,i2,i3 |
22 |
9.22 |
140 |
60 |
0,06 |
60 |
UL |
23 |
9.23 |
200 |
130 |
0,7 |
90 |
UC |
24 |
9.24 |
100 |
140 |
0,8 |
90 |
UR |
25 |
9.1 |
120 |
40 |
0,07 |
40 |
UR |
26 |
9.2 |
70 |
30 |
0,3 |
30 |
i1,i2,i3 |
27 |
9.3 |
230 |
150 |
0,9 |
110 |
i1,i2,i3 |
28 |
9.4 |
140 |
160 |
1,1 |
140 |
i1,i2,i3 |
29 |
9.5 |
160 |
120 |
0,09 |
75 |
UL |
30 |
9.6 |
250 |
80 |
1,2 |
200 |
UC |
31 |
9.7 |
150 |
100 |
0,08 |
80 |
UR |
32 |
9.8 |
130 |
90 |
1,3 |
190 |
i1,i2,i3 |
33 |
9.9 |
180 |
110 |
1,5 |
170 |
i1,i2,i3 |
34 |
9.10 |
240 |
100 |
1,4 |
180 |
i1,i2,i3 |
35 |
9.11 |
60 |
80 |
0,06 |
90 |
UL |
36 |
9.12 |
120 |
120 |
1,6 |
160 |
UC |
37 |
9.13 |
250 |
40 |
1,4 |
15 |
UR |
38 |
9.14 |
160 |
140 |
1,8 |
140 |
i1,i2,i3 |
39 |
9.15 |
140 |
30 |
0,5 |
50 |
i1,i2,i3 |
40 |
9.16 |
50 |
40 |
0,6 |
40 |
i1,i2,i3 |
41 |
9.17 |
80 |
140 |
0,15 |
130 |
UL |
42 |
9.18 |
120 |
120 |
0,1 |
120 |
UC |
43 |
9.19 |
240 |
160 |
0,25 |
100 |
UR |
44 |
9.20 |
160 |
150 |
0,5 |
180 |
i1,i2,i3 |
45 |
9.21 |
200 |
130 |
1,7 |
150 |
i1,i2,i3 |
46 |
9.22 |
180 |
160 |
0,3 |
160 |
i1,i2,i3 |
47 |
9.23 |
140 |
150 |
1 |
60 |
UL |
48 |
9.24 |
250 |
160 |
1,1 |
50 |
UC |
49 |
9.25 |
60 |
10 |
2 мГн |
5 |
i L(t);uL; uC |
50 |
9.26 |
120 |
4 |
L1=2мГн;L2=8мГн |
- |
i L1(t);uL1; uL2 |
Номер варианта |
Номер рисун-ка |
E, B |
Таблица 9.2 |
|||
R, Ом |
L, Гн |
С, мкф |
Определить |
|||
1 |
9.1 |
100 |
20 |
0,1 |
60 |
UR |
2 |
9.2 |
250 |
15 |
0,03 |
90 |
UC |
3 |
9.3 |
160 |
60 |
0,1 |
9 |
UL |
4 |
9.4 |
80 |
30 |
0,2 |
60 |
i1,i2,i3 |
5 |
9.5 |
60 |
26 |
0,09 |
50 |
i1,i2,i3 |
6 |
9.6 |
150 |
40 |
0,09 |
40 |
i1,i2,i3 |
7 |
9.7 |
90 |
30 |
0,06 |
60 |
UR |
8 |
9.8 |
120 |
20 |
0,1 |
30 |
UC |
9 |
9.9 |
180 |
50 |
0,2 |
40 |
UL |
10 |
9.10 |
50 |
30 |
0,1 |
80 |
i1,i2,i3 |
11 |
9.11 |
90 |
100 |
0,2 |
20 |
i1,i2,i3 |
12 |
9.12 |
240 |
60 |
0,07 |
10 |
i1,i2,i3 |
13 |
9.13 |
130 |
40 |
0,05 |
30 |
UR |
14 |
9.14 |
140 |
80 |
0,1 |
6 |
UC |
15 |
9.15 |
80 |
50 |
0,1 |
9 |
UL |
16 |
9.16 |
50 |
120 |
0,2 |
15 |
i1,i2,i3 |
17 |
9.17 |
140 |
80 |
0,15 |
30 |
i1,i2,i3 |
18 |
9.18 |
160 |
60 |
0,08 |
40 |
i1,i2,i3 |
19 |
9.19 |
180 |
30 |
0,15 |
60 |
i1,i2,i3 |
20 |
9.20 |
70 |
70 |
0,07 |
30 |
UR |
21 |
9.21 |
50 |
40 |
0,1 |
8 |
UC |
22 |
9.22 |
140 |
90 |
0,2 |
9 |
UL |
23 |
9.23 |
200 |
120 |
0,1 |
5 |
i1,i2,i3 |
24 |
9.24 |
100 |
40 |
0,08 |
7 |
i1,i2,i3 |
25 |
9.1 |
120 |
60 |
0,15 |
40 |
i1,i2,i3 |
26 |
9.2 |
70 |
30 |
0,05 |
30 |
UR |
27 |
9.3 |
230 |
20 |
0,1 |
60 |
UC |
28 |
9.4 |
140 |
40 |
0,09 |
30 |
UL |
29 |
9.5 |
160 |
60 |
0,2 |
30 |
i1,i2,i3 |
30 |
9.6 |
250 |
55 |
0,08 |
15 |
i1,i2,i3 |
31 |
9.7 |
150 |
100 |
0,1 |
8 |
i1,i2,i3 |
32 |
9.8 |
130 |
70 |
0,7 |
50 |
UR |
33 |
9.9 |
180 |
90 |
0,8 |
80 |
UC |
34 |
9.10 |
240 |
35 |
0,5 |
60 |
UL |
35 |
9.11 |
60 |
45 |
0,2 |
50 |
i1,i2,i3 |
36 |
9.12 |
120 |
90 |
0,7 |
80 |
i1,i2,i3 |
37 |
9.13 |
250 |
80 |
0,09 |
30 |
i1,i2,i3 |
38 |
9.14 |
160 |
40 |
0,1 |
15 |
UR |
39 |
9.15 |
140 |
60 |
0,08 |
25 |
UC |
40 |
9.16 |
50 |
75 |
0,09 |
20 |
UL |
41 |
9.17 |
80 |
30 |
0,07 |
40 |
i1,i2,i3 |
42 |
9.18 |
120 |
55 |
0,09 |
50 |
i1,i2,i3 |
43 |
9.19 |
240 |
20 |
0,06 |
60 |
i1,i2,i3 |
44 |
9.20 |
160 |
50 |
0,08 |
40 |
UR |
45 |
9.21 |
200 |
60 |
0,1 |
9 |
UC |
46 |
9.22 |
180 |
80 |
0,15 |
30 |
UL |
47 |
9.23 |
140 |
25 |
0,08 |
15 |
i1,i2,i3 |
48 |
9.24 |
250 |
45 |
0,3 |
50 |
i1,i2,i3 |
49 |
9.25 |
60 |
10 |
20 |
5 |
i L(t);uL; uC |
50 |
9.26 |
120 |
4 |
L1=2мГн;L2=20 |
- |
i L1(t);uL1; uL2 |
