
- •1 Анализ переходных процессов в линейных электрических цепях по мгновенным значениям
- •Возникновение и законы теории анализа переходных процессов
- •Классический метод анализа переходных процессов
- •Составление характеристического уравнение
- •Характер протекания свободного режима
- •2. Анализ переходных процессов в электрофизических элементах простейших электрических цепей
- •2.1 Переходной процесс в катушке индуктивности при подключении ее к источнику постоянного напряжения
- •2.2 Переходной процесс при коротком замыкании катушки индуктивности
- •2.3 Переходной процесс в катушке индуктивности при подключении ее к источнику синусоидального напряжения
- •2.4 Переходной процесс в конденсаторе при подключении его к источнику постоянного напряжения через резистор
- •2.5 Короткое замыкание rC–цепи (разрядка конденсатора)
- •2.6 Переходной процесс в конденсаторе при подключении его к источнику синусоидального напряжения через резистор
- •3. Переходные процессы в контуре с последовательным соединением резистивного, индуктивного и емкостного элементов
- •3.1 Дифференциальное и характеристическое уравнения
- •3.2 Апериодический разряд конденсатора
- •3.3 Предельный случай апериодического разряда конденсатора
- •3.4 Периодический затухающий процесс
- •3.5 Анализ переходного процесса в ветви, содержащей резистор, катушку индуктивности и конденсатор, при подключении ее к источнику постоянного напряжения
- •3.6 Анализ переходного процесса в ветви, содержащей резистор, катушку индуктивности и конденсатор, при подключении ее к источнику синусоидального напряжения
- •3.7 Включение rLc – цепи со слабым затуханием на гармоническое напряжение
- •4. Примеры анализа переходного процесса классическим методом пример 4.1
- •Решение
- •Пример 4.2
- •Решение
- •5 Анализ переходных процессов в электрических цепях с источниками напряжения произвольной формы изменения
- •5.1 Единичные и импульсные воздействия
- •Решение
- •5.2 Интеграл дюамеля
- •Решение
- •Операторный метод анализа переходных процессов
- •6.1 Основные понятия операторного метода и изображение основных электротехнических функций
- •6.2 Эквивалентные операторные схемы замещения электрофизических элементов
- •6.3 Законы ома и кирхгофа в операторной форме
- •6.4 Переход от изображения к оригиналу
- •7 Примеры анализа переходного процесса операторным методом
- •Решение
- •8 Примеры практического анализа переходных процессов
- •Решение
- •Решение
- •9 Методические указания к выполнению курсовой работы
- •Список рекомендуемой литературы
- •Содержание
Операторный метод анализа переходных процессов
Классический
метод анализа переходных процессов
имеет существенный недостаток, связанный
с громоздкостью определения постоянных
интегрирования интегрально –
дифференциальных уравнений,
составленных по второму закону Кирхгофа.
Поскольку решение интегрально –
дифференциального уравнения сводится
к решению алгебраического
характеристического уравнения, то
целесообразно систему исходных уравнений
электрической цепи записывать в виде
изображения в алгебраической форме. В
этом и заключается суть операторного
метода анализа переходных процессов,
позволяющего исключить трудоемкий
процесс определения постоянных
интегрирования. Путем введения некоторого
комплексного оператора
,
позволяющего дифференцирование и
интегрирование некоторой функции
времени
![]() свести к простым алгебраическим операциям
над изображением
свести к простым алгебраическим операциям
над изображением
![]() этой же функции. Переход от оригинала
функций времени к изображениям
производится с помощью преобразователя
Лапласа, математическое выражение
которого записывается в виде равенства
этой же функции. Переход от оригинала
функций времени к изображениям
производится с помощью преобразователя
Лапласа, математическое выражение
которого записывается в виде равенства
![]() , (6.1)
, (6.1)
где - функция времени – оригинал;
- функция переменной – изображения;
![]() - комплексная переменная.
- комплексная переменная.
С окращенно
равенство (6.1) записывается в виде
взаимного соответствия
окращенно
равенство (6.1) записывается в виде
взаимного соответствия
 ,
,
где математический знак соответствия.
Преобразование
Лапласа справедливо для сходящихся
интегралов, то есть когда модуль функции
![]() увеличивается с ростом
медленнее, чем функция
увеличивается с ростом
медленнее, чем функция
![]() .
Практически все электротехнические
функции удовлетворяют это условие.
.
Практически все электротехнические
функции удовлетворяют это условие.
6.1 Основные понятия операторного метода и изображение основных электротехнических функций
Как было отмечено выше, между оригиналом и изображением нет равенства, а есть только взаимное соответствие и из курса математики известны основные свойства прямого преобразования Лапласа.
Каждому оригиналу соответствует вполне определенное изображение, и наоборот (единственность).
И
 зображение
суммы функций равно сумме изображений
каждой из функций в отдельности
(линейность):
зображение
суммы функций равно сумме изображений
каждой из функций в отдельности
(линейность):
3 .
При умножении оригинала на число
изображение умножается на то же число
(пропорциональность):
.
При умножении оригинала на число
изображение умножается на то же число
(пропорциональность):
Из теорем операторного
исчисления для решения задач наиболее
часто используется теорема
запаздывания: функции – оригиналу,
сдвинутой вправо вдоль оси времени на
,
соответствует
ее изображение, умноженное на
![]() :
:

![]()
Изображения функций находят, вычисляя интеграл (6.1).
Так, если функция
![]() ,
где
- постоянная,
то ее изображение будет
,
где
- постоянная,
то ее изображение будет
![]() (6.2)
(6.2)
При
![]() предел функции
предел функции
![]() равен нулю; при
равен нулю; при
![]()
Чтобы получить
изображение постоянной, надо разделить
ее на
![]() (5.2).
(5.2).
Изображение
экспоненциальной функции вида
![]() .
.
Если
![]() ,
то
,
то
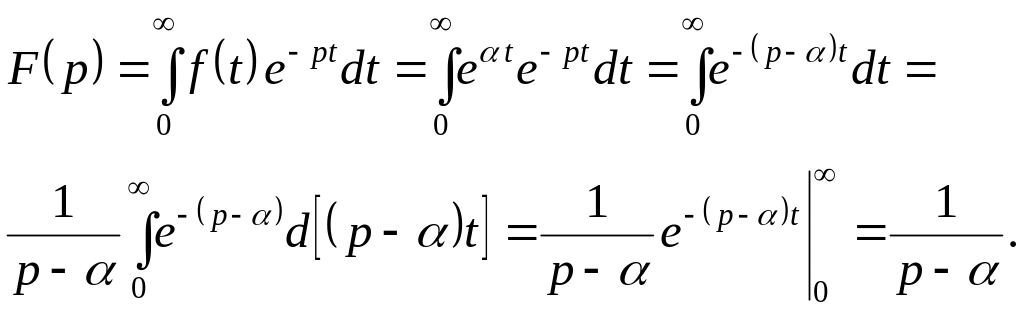
И так
так
![]() (6.3)
(6.3)
П оложив
оложив
![]() ,
получим
,
получим
![]() (6.4)
(6.4)
Изображение синусоидальной функции (без вывода)

![]() (6.5)
(6.5)
П ри
,
ри
, ![]() (6.6)
(6.6)
Изображение комплекса (без вывода)

![]() (6.7)
(6.7)
Изображение производной и интеграла (без вывода)

![]() , (6.8)
, (6.8)
где
![]() - значение оригинала при
(начальное условие)
- значение оригинала при
(начальное условие)

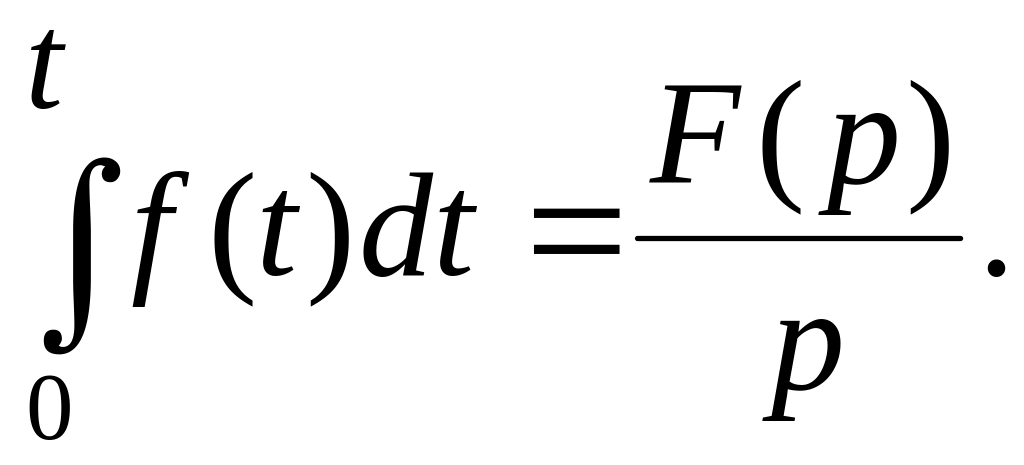 (6.9)
(6.9)
Аналогичным образом находят изображение и других функций. Пары оригинал – изображение сводят в таблицы (смотри справочник по высшей математике; раздел: операционное исчисление).
