Решение

В момент цепь включается на постоянное напряжение. Для этого случая было получено (см. формулы (2.9) и (2.10)):

;

Эти уравнения справедливы в интервале . Находим: , мА. Постоянная времени мс.

При мс имеем:

В; мА.

Строим графики функций и в интервале времени от 0 до 2 мс. В момент напряжение исчезает. С этого времени начинается свободный переходной процесс

;

.

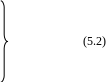
При . Подставив в уравнение , получим

В, мА.

При имеем:

В, мА.

Графики и представлены на рисунке 5.5.

5.2 Интеграл дюамеля

При использование интеграла Дюамеля необходимо предварительно рассчитать классическим способом реакцию цепи на единичное или импульсное воздействие, которые называются переходной или импульсной характеристиками цепи.

Применяя интеграл Дюамеля необходимо помнить, что интегрирование производится по текущему времени реакции, в то время, как воздействие рассматривается в текущем времени .

Суть метода заключается в замене реальной изменения напряжения ступенчатой с интервалами (рис. 5.6).

Т ок переходного про­цесса рассматривается как сумма токов, возникаю­щих под действием серии скач­ко­образ­ных из­менений напря­жений , следующих через промежутки времени в интервале от до .

Действительно, представив скачок напряжения как и приняв для выражения тока переходного процесса запишется

, (5.3)

где - переходная проводимость численно равная току при В.

В момент времени возникает скачок напряжения , вызывающий переходной процесс с током

,

где - время, соответствующее моменту скачкообразного изменения напряжения.

Тогда ток переходного процесса представляется как сумма токов, вызванных отдельными скачками напряжения, запишется следующим образом

.

При уменьшении интервалов x до бесконечно малых значений ступенчатая кривая изменения напряжения максимально приблизится к кривой , и выражение переходного тока примет вид

, (5.4)

где

Анализ переходного процесса при помощи интеграла Дюамеля выполняется в следующей последовательности:

1. определяется переходная проводимость для анализируемой цепи как ток переходного процесса при подключении ее к источнику постоянного напряжения, равного 1В;

2. определяется 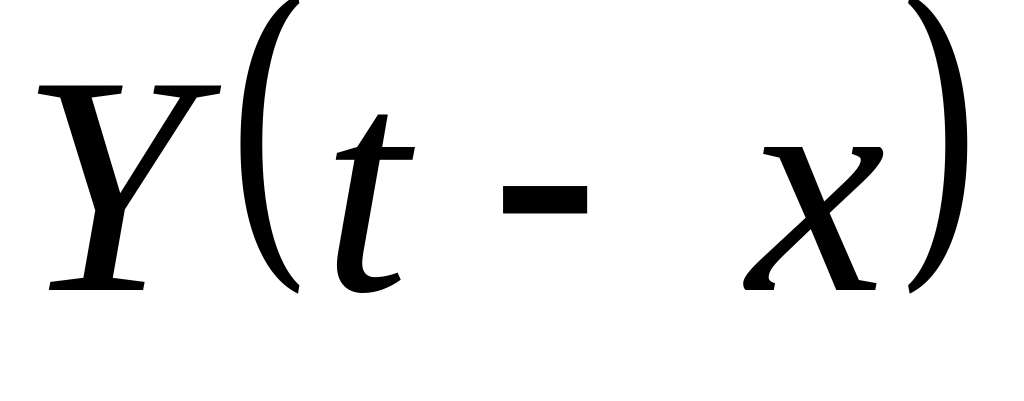путем замены в 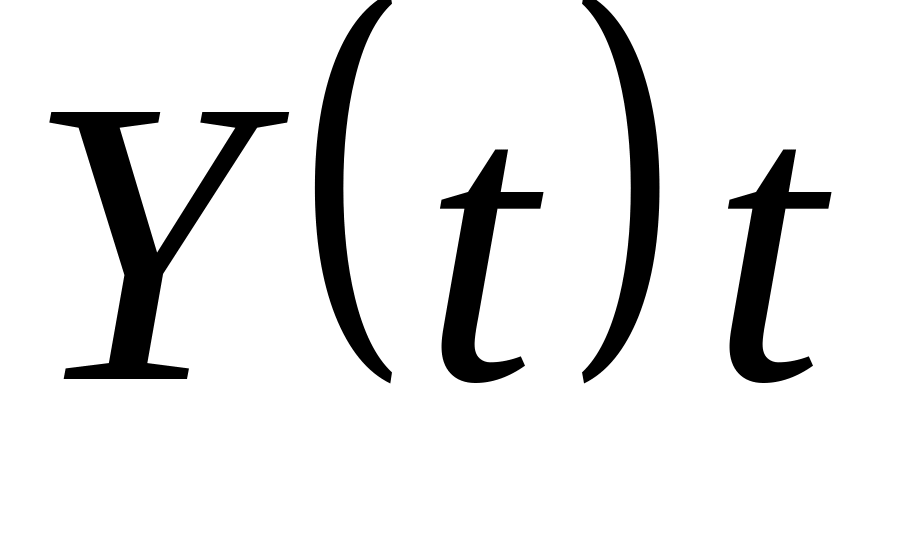на ;

3. вычисляется первая производная ;

4. полученные значения подставляются в формулу (5.4) и получается выражение тока переходного процесса.

ПРИМЕР 5.2

Определить характер изменения тока переходного процесса при подключении емкости к источнику электрической энергии с импульсным изменением напряжения через резистор R (рис. 5.7).

П араметры цепи: В; Ом; мкФ, Гц.

Решение

Находим переходную проводимость. Для чего рассчитывается ток переходного процесса в цепи при ее подключении к источнику напряжения , .

Так как в установившемся режиме ток через конденсатор не проходит , то .

Определение выражения свободного тока осуществляется с использованием выражения .

В данном случае , входное комплексное сопротивление цепи и характеристическое уравнение . Откуда показатель затухания с^-1.

Постоянная интегрирования находится из уравнения полного тока цепи при – ;

где ; .

Для нахождения воспользуемся вторым законом коммутации к уравнению второго закона Кирхгофа при начальных нулевых условиях ;

Поскольку (конденсатор до включения в цепь был разряжен), то А.

Следовательно , откуда .

Свободная составляющая .

Электрический ток А.

Следовательно, переходная проводимость находится по формуле

при В.

При – .

Находим

.

Определяем по формуле