2.2.3. Переключательная функция двух переменных

Переключательные функции двух переменных у=fк(х1,х0), где к=0,1,…,15, приведены в табл.3.3. Как видно, функции f0=0 и f15=1 не зависят от аргументов (являются константами 0 и 1); поэтому они интереса не представляют.

Таблица 3.3.

	х		у=fк(х1,х0) (к=0,1,…,15)
	x1	x0	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0123	0 0 1 1	0 1 0 1	0 0 0 0	1 0 0 0	0 1 0 0	1 1 0 0	0 0 1 0	1 0 1 0	0 1 1 0	1 1 1 0	0 0 0 1	1 0 0 1	0 1 0 1	1 1 0 1	0 0 1 1	1 0 1 1	0 1 1 1	1 1 1 1

Функции f10=x0; f12=x1 зависят только от одной переменной (они называются вырожденными функциями) и тоже не представляют интереса. Остальные десять функций являются невырожденными и каждая из них имеет свое название и обозначение.

Функция f8(x1,х0) называется конъюнкцией, функцией И, она выражает логическое произведение переменных х1 и х0 и определяется следующей таблицей истинности:

Х1	Х0	f8
0 0 1 1	0 1 0 1	0 1 0 1

Как видно из таблицы истинности, конъюнкция двух переменных равна 1 только тогда, когда обе переменные равны 1, и равна 0, если хотя бы одна из переменных равна 0. Для ее обозначения используют символ « », иногда логическое умножение обозначается точкой:

,

читается так: «f8 равно х1 и х0».

Данная функция сохраняет свой смысл и при числе переменных n2: . Устройство, реализующее конъюнкцию, называется логическим элементом И, графическое обозначение которого приведено на рис. 2.1,б.

Функция f14(х1,х0) называется дизъюнкцией, функцией ИЛИ, она выражает логическое сложение переменных х1 и х0 и определяется следующей таблицей истинности:

Х1	Х0	F14
0 0 1 1	0 1 0 1	0 1 1 1

Как видно, данная функция равна 1, если хотя бы одна из переменных равна 1, и равна 0, если все переменные равны 0.

Для обозначения дизъюнкции применяются символы « » или «+»:

F14(x1,х0)=х1 х0=х1+х0,

читается так: «f14 равно х1 или х0».

Дизъюнкция сохраняет смысл и при большем числе переменных: . Устройство, реализующее дизъюнкцию, называется ЛЭ ИЛИ и обозначается как на рис. 2.1,в.

Функция f1(x1,х0) называется функцией Пирса выражает операцию отрицания дизъюнкции (ИЛИ-НЕ).

(Записать таблицу истинности самостоятельно). Запись логического сложения с отрицанием имеет следующий вид:

.

Функция имеет смысл и при числе переменных . Устройство, реализующее данную функцию, называется ЛЭ ИЛИ-НЕ и обозначается, как показано на рис. 2.1,г.

Функция f7(x1,х0) называется отрицанием конъюнкции (И-НЕ) или функцией Шеффера и записывается следующим образом:

.

Эта функция сохраняет смысл и при числе переменных . Устройство, реализующее данную функцию, называется ЛЭ ИЛИ-НЕ и обозначается, как показано на рис. 2.1., д.

Функция f9(x1,х0) принимает значение 1 только при равенстве обоих аргументов, поэтому она называется функцией равнозначности или функцией эквивалентности и обозначается символом ~:

f9(x1,х0)=х1~х0.

Р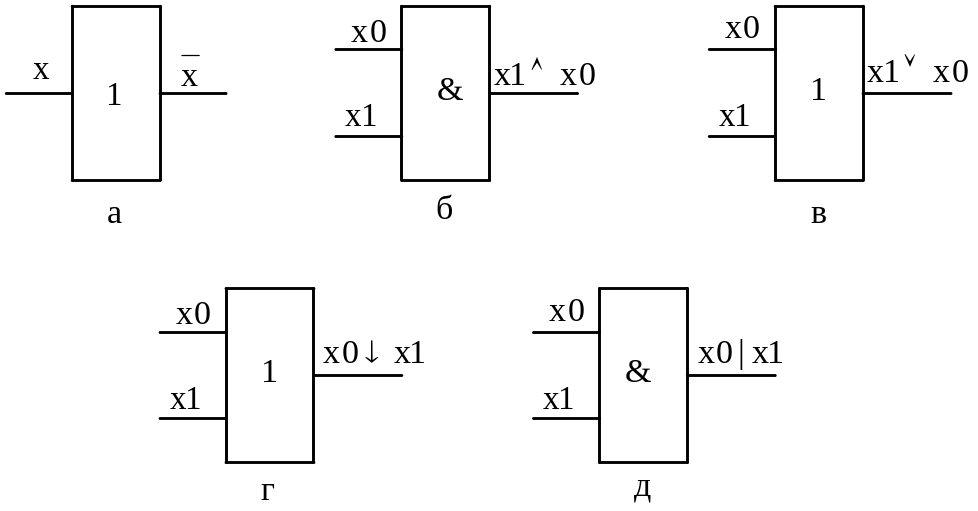 ис. 2.1.

Функция f6(x1,х0), наоборот, равна 1 только тогда, когда значения аргументов не совпадают; поэтому она называется функцией неравнозначности. Эта функция выражает сумму по модулю два; сложение по модулю 2 обозначается символом :

f6(x1,х0)=x1 x0.

Функция f2(x1,х0) называется запретом по х1. Подстановкой можно проверить, что данная функция выражается через отрицание и конъюнкцию формулой:

.

Эта функция равна х0 при х1=0 и равна 0 при х1=1.

Функция f_n(х1,х0) называется запретом по х0 (или обратным запретом) и выражается формулой

.

Эта функция при х=0 совпадает с х1, а при х0=1 равна 0.

Эта функция при х=0 совпадает с х1, а при х0=1 равна 0.

Функции f11(х1,х0) и f13(x1.х0) называются соответственно импликациями от х1 к х0 и от х0 к х1. Они выражаются через отрицание и дизъюнкцию посредством формул:

и .

Условные графические обозначения ЛЭ, реализующих функции

f9(x1,х0), f6(x1,х0), f2(x1,х0), f4(x1,х0), f11(x1,х0) и f13(x1,х0) показаны на рис. 2.3, а-е.

Рис. 2.3.

Лекция №3