ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГРАЖДАНСКОЙ АВИАЦИИ

ИРКУТСКИЙ ФИЛИАЛ

Кафедра авиационного радиоэлектронного оборудования

М. Ю. Сосновский

СХЕМОТЕХНИКА ЦИФРОВАЯ Ч.2

Курс лекций

УСТАНОВОЧНАЯ ЛЕКЦИЯ

1. Цели и задачи дисциплины

1.1. Цели изучения дисциплины

Дисциплина «Схемотехника, часть 2: Основы цифровой схемотехники» является специальной базовой дисциплиной, подготавливающей студентов к изучению других специальных и профилирующих дисциплин специальности. 160905, и имеет целью изучения принципов и методов анализа и синтеза устройств формирования, преобразования, хранения и индикации цифровых сообщений и сигналов.

1.2. Задачи изучения дисциплины

1.2.1.Иметь представление: об основных свойствах цифровых сообщений и сигналов, различных методов формирования, преобразования, хранения и индикации этих сигналов, особенностях материального отображения цифровых сигналов, технологии производства цифровых ИМС различного типа, методах и принципах выбора оптимальных решений цифровой схемотехники, временных и энергетических свойствах ИМС и узлов на них.

1.2.2.Знать: основные способы аналитического и материального представления цифровых сообщений и сигналов, сущность математических и логических действий над цифровыми сигналами и их моделями, основы теории логических функций и алгебры логики, номенклатуру, основные свойства, методы синтеза и анализа цифровых узлов комбинационного и последовательного типа, свойства и способы применения арифметико-логических устройств и устройств запоминания информации, методы анализа и синтеза устройств синхронизации, тактирования и управления цифровыми ИМС и узлами, основные принципы синтеза цифровых узлов на промышленных ИМС.

1.2.3.Уметь: осуществлять аналитическое и материальное представление цифровых сообщений и сигналов, проводить математические и логические действия над цифровыми сигналами, проводить расчет логических функций, использовать законы алгебры логики в этих расчетах, номенклатуру, технико-эксплуатационные свойства и особенности промышленных ИМС комбинационного и последовательного типа, применять арифметико-логические устройства и устройства запоминания информации, проводить анализ, синтез и электрический расчет устройств синхронизации, тактирования и управления цифровыми ИМС и узлами, читать и синтезировать структурно-логические и принципиальные схемы на основе и с применением промышленных ИМС различных технологий.

1.2.4.Иметь опыт: анализа и синтеза цифровых сигналов, синтеза цифровых устройств с использованием теории логических функций и алгебры логики, выбора и применения цифровых ИМС промышленного производства, чтения и синтеза структурно-логических и принципиальных схем на основе ИМС, расчета, анализа и синтеза устройств синхронизации, тактирования и управления цифровыми ИМС и узлами на них.

Рекомендуемая литература:

1. Основная литература

1.Бабаев В.Г. Основы цифровой схемотехники. Часть 1. МГТУ ГА, 1995.

2.Бабаев В.Г. Основы цифровой схемотехники. Часть 2. МГТУ ГА, 1996.

3.Бабаев В.Г. Основы цифровой схемотехники. Часть 3. МГТУ ГА, 1997.

4.Бабаев В.Г., Зыков В.П., Глушнев В.Г. Схемотехника импульсных и цифровых устройств. М: Воздушный транспорт, 1998.

2. Учебно-методическая литература

5.Васильева Л.С. Методические указания по применению ИМС ТТЛ-типа. МГТУ ГА, 1995.

6.Бабаев В.Г. Основы цифровой схемотехники. Часть 4. МГТУ ГА, 1998.

7. Бабаев В.Г. Пособие к выполнению лабораторных работ по дисциплине ОЦСТ. Часть 1. МГТУ ГА, 1999.

8. Сосновский М.Ю. Пособие к выполнению лабораторных работ по дисциплине ОЦСТ. Часть 2. МГТУ ГА, 2000.

9.Бабаев В.Г. Пособие к выполнению курсовой работы по дисциплине «Схемотехника», часть 2. МГТУ ГА, 2003.

10.Бабаев В.Г. Схемотехника. Пособие по изучению дисциплины, часть 2. Для студентов 4 курса спец. 201300 заочного обучения. МГТУ ГА. 2003.

Лекция №1

1. ОБЩИЕ СВЕДЕНИЯ О ЦИФРОВЫХ СИГНАЛАХ (КОДАХ)

Понятие цифрового сигнала

ЦИФРОВЫМ СИГНАЛОМ называется цифровое сообщение, преобразованное в стандартную электромагнитную форму.

ИНФОРМАЦИЯ, представленная сочетанием символов (букв, цифр) или фонемой устной речи, называется СООБЩЕНИЕ. В свое очередь, сообщение, составленное только из цифровых символов, является ЦИФРОВЫМ СООБЩЕНИЕМ. Следовательно, цифровое сообщение представляется сочетанием только цифр, а комбинации цифр, в свою очередь, представляют собой любые иные символы или понятия – буквы, слове и фразы, действия над данными (сложение, деление, возведете числа в какую-либо степень и т.д.) из которых составляется сообщение.

С помощью цифровых символов и сообщений возможна передача любой информации – книг, рисунков графиков, музыки и изображения и т.д.

Ясно, что все это должно быть произведено с использованием каких-либо стандартов кодирования сообщения и символов, передающих информацию.

Для работы с цифровым сообщением в электронных цифровых устройствах эти сообщения необходимо сначала преобразовать в бинарную форму, используя только два символа «0» и «1», а затем в цифровой сигнал (в дальнейшем будем подразумевать «1» = I – логическое состояние, а не число).

Преобразование цифрового сообщения в цифровой сигнал называется КОДИРОВАНИЕМ СООБЩЕНИЙ. Поэтому цифровые сигналы называются иначе цифровыми кодами чисел.

Для получения сигнала из цифрового сообщения используются соглашения положительной, отрицательной или импульсной логики.

U(t)

t

U¹

U⁰

Рис. 1.1. Соглашение положительной логики

Соглашение положительной логики применяется на практике в большинстве интегральных микросхем (ИМС) транзисторно-транзисторной логики (ТТЛ - типа).

Напряжения более 2,4 В отображают логическую " 1 ", а напряжения менее 0,4 В отображают логический " 0 ". На рис. 1.2. показан цифровой сигнал, отображающий число 26₁₆ = 0100110.

Рис. 1.2. Цифровой сигнал числа 26₁₆

Цифровые сигналы можно условно разделить на две группы:

1) стандартные (типовые) сигналы: они отображают стандартные символы (буквы, цифры, арифметические или логические операции, знаки препинания и т.д.) и образуется с помощью стандартных цифровых кодов;

2) цифровые сигналы, отображающие количественную характеристику какого-либо процеcca: расстояние от самолета до аэропорта, высоту полета ЛА и т.д. Другими словами цифровые сигналы – текущие данные о каком-либо процессе в определенный момент времени.

Как правило, такие данные получают от различных датчиков, параметрами которых могут быть: время, длина, частота, фаза и т.д.

Для учета и дальнейшей обработки таких сигналов их необходимо преобразовать в цифровой код при помощи аналого-цифрового преобразователя (АЦП).

На вход АЦП подаётся аналоговый электрический сигнал, например, от бортового радиовысотомера (РВ). При поступлении на синхровход АЦП тактового импульса, на выходе АЦП формируется цифровой код, соответствующий напряжению сигнала (в данном случае – высота полета самолета в каждый момент времени).

Позиционные числа

Позиционным называется число, у которого весовой коэффициент любого разряда определяется его позицией (номером разряда).

Вес для целых чисел определяется:

H_i = q^i-1,

где q – основная система счисления;

i – номер разряда числа (имеется ввиду наименьший значащий разряд (МЗР); i =1, а старший (СЗР) – номер i =n).

Для десятичных чисел q = 10; вес первого разряда H₁ = 10⁰, H₂ = 10¹, H_n = 10^n-1.

Для двоичных чисел q = 2; вес первого разряда H₁ = 2⁰, H₂ = 2¹, H_n = 2^n-1 и т.д.

Общая формула позиционного числа:

А = ,

где n – число разрядов целой части; i = 1, 2,…n;

a_i – цифры разрядов целой части;

m – число разрядов дробной части; j = 1, 2,…m;

a_j - цифры разрядов дробной части.

Сокращенная запись числа А:

A = a_n ·a_n-1·a_n-2… a₂·a₁,·a_m·a_m-1·a_m-2…a₂·a₁.

Арифметические операции над двоичным числом

Сложение двух двоичных чисел

При сложении двоичных чисел используется правило двоичной арифметики 0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 0 плюс 1 переноса в соседний разряд , 1 + 1 + 1 = 1 плюс 1 переноса в соседний разряд.

Пример: 111111 1 - переносы

А = 110110,011

+ В = 101101,110

А + В = 1100100,001.

Следует помнить, складывая два n- разрядных числа, получаем сумму, которая может иметь на один разряд больше.

Сложение двоичных чисел, как видно из примера, фактически сводится к сложению числа единиц, имеющихся в каждом разряде слагаемых c учетом единиц переноса.

Сложение более двух двоичных чисел

При сложении трех, четырех и т.д. двоичных чисел в разрядах слагаемых может образоваться с учетом переносов 4–7 единиц. Сложение такого числа единиц подчиняется общему правилу: число единиц необходимо записать в двоичном виде, при этом младший разряд полученного двоичного числа записывается в том разряде суммы, где образовано складываемое число единиц, остальные разряды двоичного числа определяют расположение единиц переносов. Сложение четырех единиц дает: I + I + I + I = I00₂ = 4, в разряд суммы записываем ноль и образуем единицу переноса через разряд и т.д.

Умножение двоичных чисел

Умножение двоичных чисел производится по тому же правилу, что и умножение десятичных чисел. Учитывая, что в разрядах множителя записываются только цифры 0 или I, легко сформулировать правило умножения двоичных чисел:

1) Записываем множимое и множитель так, чтобы их разряды с одинаковым " весом " находились один под другим:

А = 10101,01 – множимое

х В = 10011,10 – множитель

………..

2) Определяем число единиц в множителе и их местоположение.

3) Множимое переписываем справа – налево (его запятая игнорируется), нанимая с местоположения единицы множителя, и делаем это столько раз, сколько единиц в множителе.

4) Складываем арифметически полученные двоичные числа, их количество равно числу единиц множителя.

5) Местоположение запятой в произведении определяется суммой разрядов после запятой множимого и множителя.

Пример : 1101,01 = А

х 0101,01 = В

1101 01

+ 110101

+ 110101

А х В = 1000101,10 01

переносы: 11111 1

Вычитание двоичных чисел

Вычитание легко представить как алгебраическое сложение:

А – В = А + (–В)

Следовательно, для осуществления алгебраического сложения необходимо ввести знаковые разряды: положительные числа имеют знаковый разряд " 0 ", отрицательные числа – знаковый разряд " 1 ". Кроме того, отрицательные числа представляются в обратном коде, для этого все разряды числа, кроме знакового, инвертируются: 0 заменяют на 1 и наоборот.

Пример: А = 10111,011

В прямом коде –A = 110111,011

В обратном коде – А = 101000,100

Деление двоичных чисел

Деление двоичных чисел производится по тому же правилу, что и деление десятичных чисел. Как известно, при делении десятичных чисел делается вычитание из одного десятичного числа другого с использованием правила «заема» единиц в соседних, более старших разрядах.

Пример: 99 : 11 = 9 1100011 : 1011 = 1001

– 1011

0001011

– 1011

0000

Преобразование целых чисел

Для преобразования целой части числа разделим левую и правую части полинома на основание q:

А_ц/q = a_n q^n-2 + a_n-1 q^n-3 +…a₂ q⁰ + a₁/q.

Выполняя последовательно операцию деления на q, получим новое целое число и остаток от деления с цифрой разряда a_n-1.

#₁ 100:8 = 12:8 =1; Ответ: 100 = 144₈.

4. 4

#₂ 89:2 = 44:2 = 22:2 = 11:2 = 5:2 = 2:2 = 1:2; Ответ: 89:2 = 1011001

1 0 0 1 1 0 1

Для получения восьмеричного числа из двоичного числа нужно разбить его разряды на «триады»:

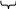А = 010 011 101 011 = 2353₈.

2 3 5 3

Для получения двоично-восьмеричного кода нужно каждую цифру восьмеричного числа заменить трёхразрядным двоичным числом:

2353₈ = 2·8² + 3·8¹ + 5·8⁰ = 128 +24 + 1.

В шестнадцатеричных числах основание q = 16; алфавит включает числа 0÷9 и буквы A÷F (10÷15).

Получение шестнадцатеричных чисел из двоичных

A = 1101 1001 1110, 0001 0101 = D9E, 15₁₆.

D 9 E 1 5

Целую часть числа разбиваем на тетрады (четырех - разрядные числа), от запятой справа – налево, а дробную часть – тетрады, от запятой слева – направо. Полученные тетрады заменяем цифрами.

Шестнадцатеричные числа есть компактная запись двоичных чисел

Бинарно-десятичные коды десятичных чисел

Бинарный код числа – код, использующий только два символа: 0 и 1.

Существуют следующие бинарные коды:

1. натуральный двоичный код (НДК) или иначе двоичные числа;

2. бинарные коды 8-ричных и 16-ричных чисел;

3. двоично-десятичный код (ДДК) чисел;

4) специальные бинарно-десятичные коды чисел.

Лекция №2