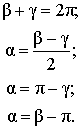22.Взаимное расположение прямой и окружности.

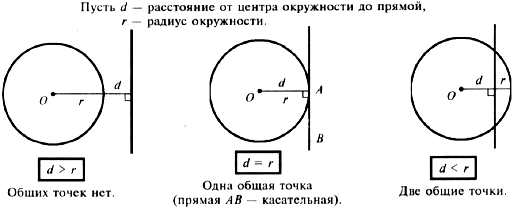
23.Касательная к окружности

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

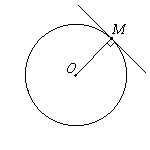
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

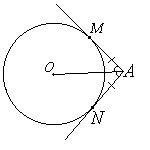
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

24.Центральные и вписанные углы

Определение 1. Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами (рис. 1).

Рис. 1

Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами (рис. 2).

Рис. 2

25. Теорема о двух пересекающихся хордах

Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

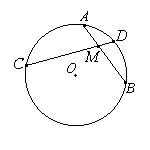
26. Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами		Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Угол, образованный секущими, которые пересекаются вне круга		Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Угол, образованный касательной и хордой, проходящей через точку касания		Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
Угол, образованный касательной и секущей		Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами
Угол, образованный двумя касательными к окружности		Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами