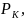4. Связь плоской задачи теории фильтрации с теорией функций комплексного переменного

При исследовании плоского фильтрационного потока, подчиняющегося закону Дарси, можно использовать теорию функций комплексного переменного. Совместим плоскость комплексного переменного 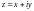с основной плоскостью течения.

Для каждого плоского фильтрационного потока можно найти характеристическую функцию течения, или комплексный потенциал F(z), который является функцией комплексного переменного z. В функции F(z) можно отделить действительную часть от мнимой:

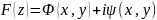(1.4.1)

где 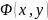- потенциал скорости; 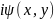- функция тока. Эти функции связаны между собой уравнениями Коши – Римана:

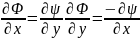(1.4.2)

и подчиняются уравнению Лапласа:

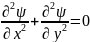(1.4.3)

Рисунок 1.4.1 - Эквипотенциали и линии тока.

Уравнение 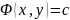определяет собой семейство эквипотенциалей, совпадающих с изобарами, так как 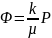, а 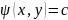- семейство линийтока.

Эквипотенциали и линии тока взаимно ортогональны (рис. 1.4.1).

Проекции скорости фильтрации на координатные оси находятся по формулам

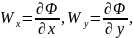(1.4.4)

а модуль скорости фильтрации

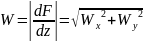(1.4.5)

Время движения частицы жидкости вдоль линии тока s можно определить по формуле:

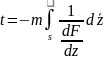(1.4.6)

где 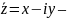сопряженное с 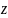комплексное переменное.

Если какой-либо сложный плоский фильтрационный поток можно представить как результат наложения нескольких простейших потоков, то характеристическая функция сложного потока равна, по принципу суперпозиции, алгебраической сумме характеристических функций простейших потоков[1].

2. Расчетная часть

2.1. Задача № 1: «Исследование прямолинейнно-параллельного установившегося фильтрационного потока несжимаемой жидкости по закону Дарси в однородном пласте (приток к галерее)»

Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит галереи, закон движения частиц жидкости и средневзвешенное по объему порового пространства пластовое давление при следующих исходных данных:

Таблица 2.1.1 - Исходные данные для расчетов.

МПа		МПа		км		µ, мПа	В, м	h, м	m, %
9,6		7,1		9,0	0,8	2,0	140	8	18

где

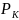– давление на контуре питания;

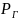– давление на стенке галереи;

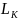– длина пласта;

– проницаемость;

µ – динамическая вязкость жидкости;

В – ширина пласта;

h – толщина пласта;

m – пористость.

Рисунок 2.1.1 - Схема прямолинейно–параллельного фильтрационного потока в пласте.

Решение:

1. Определение закона распределения давления:

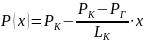(2.1.1)

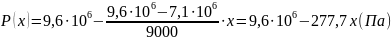
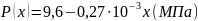
Р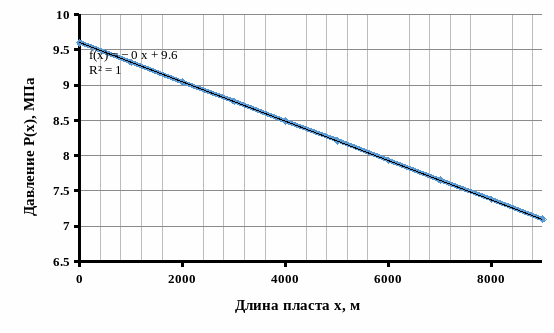 исунок 2.1.2 - График распределения давления в пласте .

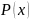2. Определение градиента давления:

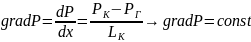(2.1.2)

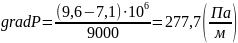
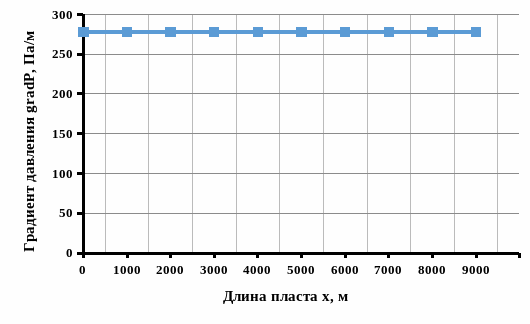
Рисунок 2.1.3 - График распределения градиента давления в пласте gradP(x).

3. Определение скорости фильтрации:

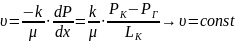(2.1.3)

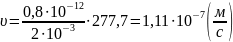
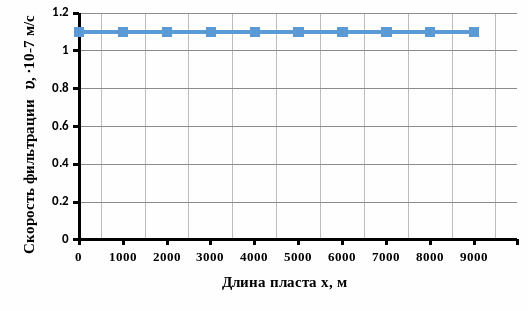
Рисунок 2.1.4 - График распределения скорости фильтрации в пласте .

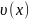4. Определение дебита галереи:

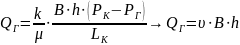(2.1.4)

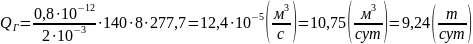
*Пересчет дебита в весовых единицах был произведен при .

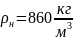5. Определение закона движения частиц жидкости:

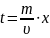(2.1.5)

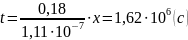
Тогда время прохождения частиц в пласте будет равным:

6. Средневзвешенное по объему порового пространства пластовое давление:

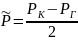(2.1.6)

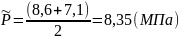
7. Минимальная верхнекритическая скорость фильтрация жидкости, при которой нарушается закон Дарси:

Формула В.Н.Щелкачева: 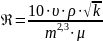(2.1.7)

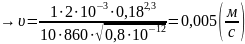
Вывод: при исследовании прямолинейнно-параллельного установившегося фильтрационного потока несжимаемой жидкости по закону Дарси в однородном пласте градиент давления и скорость фильтрации в пласте постоянны, а давление в пласте уменьшается равномерно по мере отдаления от скважины. Были рассчитаны : градиент давления, скорость фильтрации, дебит галерии, средневзвешенное пластовое давление, значения которых:

• ,

• ,

• ,

• .
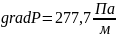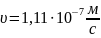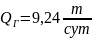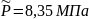