2. Кинетическая потенциальная и полная энергия гармонических колебаний

Энергия гармонических колебаний

Колеблющееся тело обладает кинетической и потенциальной энергией.

Кинетическая энергия колеблющейся материальной точки с массой m вычисляется по формуле (1.29) с учетом (3.11):

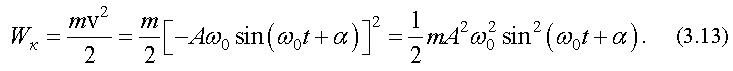
Потенциальная энергия материальной точки, совершающей колебания под действием упругой силы вычисляется по формуле (1.32) с учетом (3.9) и (3.7)

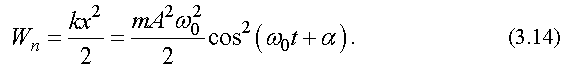
Полная энергия гармонических колебаний равна

Учитывая, что   получим

Из формулы (3.15) следует, что полная энергия при гармонических колебаниях не зависит от времени, т. е. остается постоянной. Следовательно, выполняется закон сохранения механической энергии.

Второй важный вывод: энергия при гармонических колебаниях пропорциональна квадрату амплитуды и квадрату частоты.

Векторная диаграмма

При рассмотрении многих вопросов, в частности, при сложении колебаний одинакового направления и частоты бывает удобно гармоническое колебание представить в виде векторной диаграммы. Векторная диаграмма строится следующим образом: надо изобразить вектор, длина которого равна амплитуде, угол наклона к оси абсцисс равен начальной фазе. Если привести этот вектор во вращение с угловой скоростью ω₀, равной круговой частоте колебаний, то проекция его конца на выбранную ось будет изменяться по гармоническому закону.

На рис. 3.3 представлена векторная диаграмма для гармонического колебания

в момент времени t = 0.

Рис.3.3

3. Силы вызывающие гармонические колебания.

Поскольку при гармонических колебаниях

А = -ω₀²х,

то, следовательно, возвращающая сила F равна

F – ma = -mω₀²x.

Итак, гармонические колебания вызываются упругими силами. Напомним, что упругими называют силы, величина которых пропорциональна смещению

F_упр = -kx/

Коэффициент упругости k имеет размерность

и зависит только от материала пружины.

Очевидно, k = mω₀², откуда следует, что собственная частота гармонических колебаний зависит только от отношения коэффициента упругости к массе колеблющегося тела.

.

Система, совершающая гармонические колебания, называется гармоническим осциллятором. Период собственных колебаний гармонического осциллятора определяется отношением массы m к коэффициенту упругости системы k:

Формулу ω₀² =k/m можно записать в виде

Возвращающая сила и смещение в маятнике показаны на рис. 8.

Для маятника х = lsinΘ; F_возвр. = mgsinΘ.

Рис. 8. Смещение х и возвращающая сила F_возвр в маятнике

Поэтому

,

откуда следует

.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. На одинаковых пружинах висят грузы m₁ и m₂ – см. рис. 9, причем m₂ > m₁. У какого груза период колебаний больше?

2. На разных пружинах висят грузы m₁ и m₂ (m₂ > m₁) – см. рис. 10. При подвешивании грузов оказалось, что удлинения пружин одинаковы. Для какого груза период колебаний будет больше?

Рис. 9 Рис. 10

4. Сложение колебаний одного направления.

 Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (А₁ ≠ А₂, φ₀₁ ≠ φ₀₂):

, .

Результирующее движение, равное сумме колебаний х₁ и х₂, будет гармоническим колебанием той же циклической частоты ω:

. (11.10)

Рис. 11.3.

Определим амплитуду и начальную фазу результирующего колебания методом векторных диаграмм. Для этого проведем из точки О векторы  и  под углами φ₀₁ и φ₀₂ к оси Ох и приведем их во вращение с угловой скоростью ω (рис. 11.3).

Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому угол φ₂ – φ₁ между ними все время остается неизменным. Проекции векторов  и  на ось Ох совершают гармонические колебания. Результирующее колебание будет изображаться проекцией на ось Ох вектора  , полученного из векторов  и по

правилу параллелограмма. Из построения на рис. 11.3 следует, что (по теореме косинусов)

,

. (11.11)

Из треугольников ∆ОА₁В и ∆ОАС для начальной фазы φ₀ результирующего колебания следует выражение

. (11.12)

Рассмотрим частные случаи сложения колебаний.

1а.  ,

то есть, если разность фаз складываемых колебаний равна четному числу π, то тогда колебания максимально усиливают друг друга.

1б.  ,

то есть, если разность фаз складываемых колебаний равна нечетному числу π, то тогда колебания максимально ослабляют друг друга.

2. Биения –это колебания, которые возникают в результате сложения двух гармонических колебаний х₁ и х₂ одного направления с близкими частотами (ω₂, ω₁ >> ∆ω = ω₂ – ω₁):

.

Рассмотрим подробнее результаты сложения таких колебаний. Для простоты будем считать, что амплитуды складываемых колебаний одинаковы: А₁ = А₂ = А. Используя известную формулу сложения косинусов, получим:

и определим:

. (11.13)

Первый сомножитель в выражении (11.13) изменяется со временем значительно медленнее второго (∆ω << ω₁, ω₂), поэтому можно считать, что результирующее колебание представляет собой колебание с циклической частотой ω = (ω₁ + ω₂)/2 и с изменяющейся со временем амплитудой биений:

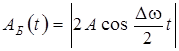. (11.14)

Итак, биения можно представить как колебания с периодически изменяющейся амплитудой; эти колебания не являются гармоническими. При этом период изменения амплитуды (период биений Т_Б) и циклическая частота биений Ω будут определяться по формулам:

. (11.15)

На рис. 11.4 приведены графики изменения амплитуды биения А_Б и смещения х м. т. от времени. Метод биений применяют, например, для настройки музыкальных инструментов.