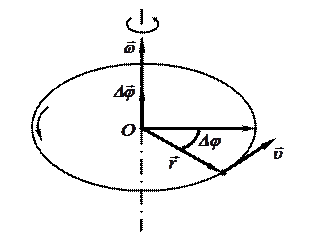- •7. Массой тела называют физическую величину, являющуюся мерой его инерционных свойств.
- •Современная формулировка
- •Историческая формулировка
- •19. Закон сохранения механической энергии.
- •20. Применение законов сохранения к столкновению упругих и неупругих тел.
- •210 Вращательное движение абсолютно твердого тела
- •22.Момент импульса
- •23. Кинетическая энергия вращающегося тела
- •24. Общие свойства жидкости и газа
- •25. Вязкая жидкость силы внутреннего трения
- •2. Механические колебания и волны в упругих средах.
- •2. Кинетическая потенциальная и полная энергия гармонических колебаний
- •Силы вызывающие гармонические колебания.
- •Сложение колебаний одного направления.
- •5.Сложение взаимно перпендикулярных колебаний.
- •29. Понятие волны. Продольные и поперечные волны. Энергия бегущей волны. Вектор Умова. Стоячие волны.
- •6. Затухающие колебания дифференциальное уравнение
- •2.2. Декремент затухания и логарифмический декремент затухания.
- •7.Вынужденные колебания
- •8. Волновые процессы. Продольные и поперечные волны
- •3.Молекулярная физика и термодинамика
- •1. Изопроцессы и закономерности их протекания.
- •2.Идеальный газ.
- •3. Закон Максвела
- •§5 Экспериментальная проверка закона распределения Максвелла - опыт Штерна
- •§6 Барометрическая формула
Физические основы механики
1.Механическое движение – это процесс изменения положения данного тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условно принятое за неподвижное – тело отсчета.
Тело отсчета – это тело, относительно которого опре-деляется положение другого тела.
Обычно в качестве тела отсчета выбирается земля, но может быть и движущийся относительно земли предмет: автомобиль, лодка, самолет и т.д.

Рис. 1.
Пример. Автомобиль (рис. 1) движется относительно тела отсчета – дерева. Человек вместе с автомобилем движется относительно этого тела отсчета, но относительно другого тела отсчета (автомобиль) находится в покое.
Механическое движение всегда относительное.
Механический покой всегда относительный.
Система отсчета – это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Простейшей системой координат является прямоугольная декартова система (рис. 2). Система координат нужна для определения положения тела относительно тела отсчета. Выбор системы отсчета зависит от условий дан-ной задачи.
Рис. 2.
Движение реальных тел, как правило, сложное. Для упрощения рас-смотрения движений пользуются моделями. Одними из первых моделей реальных тел являются абсолютное твердое тело и материальная точка.
Абсолютно твердым телом называется тело, рас-стояние между любыми двумя точками которого остается постоянным при любых внешних воздействиях.
Эта модель позволяет исключить деформацию тел при движении. Изу-чив движение абсолютно твердого тела, мы понимаем закономерности движения реальных твердых тел.
Простейшими видами механического движения абсолютно твердого тела являются поступательное (рис. 3) и вращательное (рис. 4).

Рис. 3

Рис. 4
Поступательным движением называется движение, при котором любая прямая, соединяющая две произ-вольные точки тела, перемещается параллельно самой себе. При поступательном движении траектории всех точек тела одинаковы. Таким образом, для описания поступательного движения тела достаточно описать движение какой-либо одной его точки (т.е. рассмотреть кинематику прямолинейного движения материальной точки).
Вращательным движением называется такое движе-ние, при котором все точки тела описывают окружности в параллельных плоскостях, а центры этих окружностей лежат на одной прямой, называемой осью вращения (неподвижная ось – рис. 3). Любое плоское движение можно представить как результат поступательного движения вдоль ВВ' и «чистого вращения» на угол А'В'А'' – рис. 4. Изучая характер движения Земли, планет относительно Солнца, мы можем не учитывать размеры этих тел и считать их материальными точками (т.е. рассмотреть кинематику криволинейного движения материальной точки).
Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. Данное понятие является математической абстракцией. Одно и то же тело в одних задачах можно рассматривать как материальную точку, а в других задачах – нельзя. Например, радиус Земли RЗемли равен 6400 км, расстояние между Солнцем и Землей L равно 150 000 000 км (L >> RЗемли). Рассматривая движение Земли относительно Солнца, радиусом Земли можно пре-небречь и считать, что Земля – материальная точка. Однако если нужно выяснить причины смены времен года, то Землю уже нельзя считать матери-альной точкой, а надо учитывать ее размеры, вращение вокруг оси и т.д. Мы будем изучать механическое движение материальной точки для того, чтобы потом определить движение реального тела.
2. Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется прямолинейнымравномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроецировать на ось OX и рассматривать их проекции как алгебраические величины.
Прямолинейное
равномерное движение, ![]() ,
, ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
(2.9)
,
(2.9)
где ![]() -
перемещение;
-
перемещение;![]() -
пройденный путь;
-
пройденный путь;![]() -
координата в момент времени t;
-
координата в момент времени t; ![]() -
координата в начальный момент времени t=0.
Зависимость координаты x от
времени t линейная,
график зависимости x(t)
представляет собой прямую линию.
-
координата в начальный момент времени t=0.
Зависимость координаты x от
времени t линейная,
график зависимости x(t)
представляет собой прямую линию.
Прямолинейное
равнопеременное движение, ![]() :
:
![]() ,
, ![]() ,
(2.10)
,
(2.10)
![]() ,
, ![]() ,
(2.11)
,
(2.11)
где х
– координата
движущейся точки в момент времени t; x0 –
координата в момент времени ![]() ;
; ![]() -
проекции соответствующих векторов на
ось х.
-
проекции соответствующих векторов на
ось х.
При использовании путевого способа описания движения зависимость пройденного пути s и зависимость величины скорости v от времени будут иметь вид:
![]() ,
, ![]() .
(2.12)
.
(2.12)
Следует помнить, что этими уравнениями можно пользоваться при условии, что при равнозамедленном движении (в формулах ставятся знаки «минус») направление движения на заданном промежутке времени не меняется.
Зависимость
проекции скорости ![]() от
времени является линейной, график
зависимости имеет вид прямой линии. По
наклону графика скорости может быть
определена проекция ускорения aх .
от
времени является линейной, график
зависимости имеет вид прямой линии. По
наклону графика скорости может быть
определена проекция ускорения aх .
Зависимость
координаты x(t) от времени является
квадратичной, график зависимости
является параболой. Вершина параболы
соответствует моменту времени, когда
направление движения меняется на
противоположное. Зависимость пути ![]() от
времени тоже является квадратичной, но
только с течением времени пройденный
путь всегда возрастает.
от
времени тоже является квадратичной, но
только с течением времени пройденный
путь всегда возрастает.
3. Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории. Положение движущейся точки на траектории задается радиус-вектором r, проведенным в эту точку из какой-либо неподвижной точки О, например, начала координат (рис. 1.2). Пусть в момент времени t материальная точка находится в положении М с радиус-вектором r = r(t). Спустя короткое время Dt, она переместится в положение М1 с радиусом – вектором r1 = r(t+Dt). Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью Dr = r1 - r. Средней скоростью движения за время Dt называется величина
![]() .
(1.8)
.
(1.8)
Направление средней скорости Vср совпадает с направлением вектора Dr.
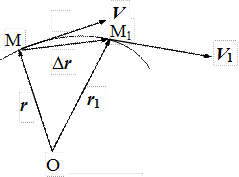
Рис. 1.2
Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени
![]() (1.9)
(1.9)
называется истинной или мгновенной скоростью материальной точки. Вектор V направлен по касательной к траектории движущейся точки.
Ускорением а называется вектор, равный первой производной вектора скорости V или второй производной радиуса – вектора r по времени:
![]() (1.10)
(1.10)
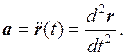 (1.11)
(1.11)
Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О1 будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис. 1.3).

Рис. 1.3.
Конец вектора V называется скоростной точкой. Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу.
Рис. 1.2 отличается от рис. 1.3 только обозначениями. Радиус – вектор r заменен на вектор скорости V, материальная точка – на скоростную точку, траектория – на годограф. Математические операции над вектором r при нахождении скорости и над вектором V при нахождении ускорения совершенно тождественны.
Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу. Следовательно, все соотношения и теоремы, полученные для скорости, остаются справедливыми и для ускорения, если в них произвести замену величин и терменов согласно следующей таблице:
Материальная точка Радиус – вектор Траектория Скорость |
® ® ® ® |
Скоростная точка Вектор скорости Годограф Ускорение |
В
качестве простейшего примера найдем
ускорения точки, равномерно вращающейся
по окружности радиуса r (Рис.1.4.а).
Скорость V направлена
по касательной к окружности, ее величина
определяется выражением ![]() .
Годоргафом будет окружность
радиуса V (Рис.1.4.б).
Когда материальная точка М вращается
по окружности радиуса r,
соответствующая ей скоростная
точка А вращается
в том же направлении по окружности
радиуса V,
описывая эту окружность за то же время Т.
Положениям материальной точки на
траектории М1, М2, М3, М4 соответствуют
на годографе положения скоростной
точки А1, А2, А3, А4 .
Ускорение а направлено
по касательной к окружности – годографу
и притом к центру О траектории
вращающейся точки М.
По аналогии с формулой
,
для величины ускорения можно написать
.
Годоргафом будет окружность
радиуса V (Рис.1.4.б).
Когда материальная точка М вращается
по окружности радиуса r,
соответствующая ей скоростная
точка А вращается
в том же направлении по окружности
радиуса V,
описывая эту окружность за то же время Т.
Положениям материальной точки на
траектории М1, М2, М3, М4 соответствуют
на годографе положения скоростной
точки А1, А2, А3, А4 .
Ускорение а направлено
по касательной к окружности – годографу
и притом к центру О траектории
вращающейся точки М.
По аналогии с формулой
,
для величины ускорения можно написать
 .
(1.12)
.
(1.12)

а) б)
Рис. 1.4
(1.12) есть центростремительное ускорение. Ее можно записать в векторной форме
![]() .
(1.13)
.
(1.13)
Знак минус указывает на то, что направления векторов а и r взаимно противоположны, т.е. ускорение а направлено к центру круговой траектории, по которой вращается материальная точка. Можно также написать для любого положения движущейся точки
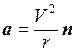 ,
(1.14)
,
(1.14)
где n – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру О (см. рис.1.4а).
Имея
в виду дальнейшие обобщения, представим
вектор скорости в виде V= Vt,
где t-
единичный вектор касательной к окружности.
Первый множитель V дает
численную величину скорости, второй
множитель t указывает
ее направление. При равномерном вращении
абсолютное значение скорости V остается
неизменным, меняется только направление
скорости, т. е. единичный вектор t.
Дифференцированию подлежит только этот
вектор, а потому ![]() .
Сравнивая это выражение с (1.14), получим
.
Сравнивая это выражение с (1.14), получим
![]() .
(1.15)
.
(1.15)
Формулу (1.15) можно использовать в случе произвольной гладкой кривой. Здесь необходимо ввести два новых понятия: величина 1/r и единичный вектор n. Величина 1/r называется кривизной кривой, r – радиусом кривизны, а n – единичным вектором главной нормали к кривой. При этом кривизна 1/r считается существенно положительной. А потому единичный вектор n всегда направлен сторону вогнутости кривой.
Рассмотрим общий случай движения материальной точки по криволинейной траектории. Запишем вектор скорости в виде V = Vt. Продифференцировав правую и левую часть по времени, получим
![]() ,
(1.16)
,
(1.16)
или, с учетом формулы (1.15),
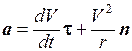 .
(1.17)
.
(1.17)
Ускорение а направлено под углом к траектории. Первое слагаемое в формуле (1.17)
![]() (1.18)
(1.18)
есть вектор, направленный по касательной к траектории. Этот вектор называется касательным или тангенциальным ускорением. Второе слагаемое
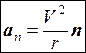 (1.19)
(1.19)
есть вектор, направленный вдоль главной нормали в сторону вогнутости траектории. Он называется нормальным ускорением. Таким образом, в общем случае ускорение аможно представить в виде геометрической суммы тангенциального и нормального ускорения:
![]() .
(1.20)
.
(1.20)
Тангенциальное ускорение меняет скорость только по величине, нормальное ускорение меняет ее только по направлению.
Модуль полного ускорения точки
 .
(1.21)
.
(1.21)
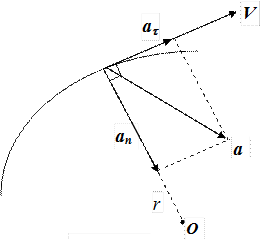
Рис. 1.5
Направления полного ускорения и его составляющих (аt, аn) для случая ускоренного движения приведены на рис. 1.5. При замедленном движении вектор аt имеет противоположноенаправление.
Характеристика движения материальной точки в зависимости
от тангенциальной и нормальной составляющих ускорения
|
|
Движение |
|
|
Прямолинейное равномерное |
const |
|
Прямолинейное равнопеременное |
|
const |
Равномерное по окружности |
|
|
Равномерное криволинейное |
const |
0 |
Криволинейное равнопеременное |
Табл. 1.1
Поступательное движение. Это такое движение тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.
При поступательном движении все точки тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Таким образом, поступательное движение тела может быть полностью описано, если известны зависимость от времени радиуса - вектора r (t) любой точки этого тела и положение последнего в начальный момент.
1. Может ли криволинейное движение быть равномерным?
2. Чему равно скалярное произведение скорости и ускорения в случае равномерного движения по окружности?
3. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
4. В каких случаях модуль перемещения точки равен длине пути, пройденного точкой за тот же промежуток времени?
5. Как движется точка, если скорость этой точки все время ортогональна ее ускорению?
6. Какова траектория плоского движения точки, если ее радиальная скорость равна нулю?
Задачи
1. Можно ли утверждать, что точка движется без ускорения в случаях:
а) u = const; б) u= const?
2. Является ли движение точки обязательно прямолинейным в случаях:
а) u= const; б) a= const?
3. Точка движется равномерно по окружности. Начало ее радиус-вектора r совпадает с центром окружности. Отличны ли от нуля выражения dr/dt и dV/dt?
4. При каком движении материальной точки выполняются соотношения at = 0, an = const ¹ 0: а) при равномерном движении по окружности; б) при равномерном движении по винтовой линии; в) при равномерном прямолинейном движении; г) при равнопеременном движении по окружности?
1) а, б, в; 2) а, б; 3) г; 4) а; 5) а, б, г.
5. Применима ли для вычисления тангенциального ускорения формула at = u/t в случаях: а) u= 2t + 6; б) u = 3t2; в) u = 5t (u– в м/с; t – в с)?
6. Математический маятник совершает гармонические колебания. Отличны ли от нуля в крайней точке траектории маятника:
а) нормальное ускорение; б) тангенциальное ускорение?
7. Тело бросили вертикально с некоторой высоты: а) вверх;
б) вниз. Начальные скорости в обоих случаях одинаковы. Сравнить скорости в момент падения тела на землю. Сопротивлением воздуха пренебречь.
8. Какой график скорости соответствует графику пути на рисунке?


9. Применима ли для вычисления углового ускорения формула e = w/t в случаях: а) w = 2t + 8; б) w = 9t; в) w = 6 (w – в рад/с, t – в с)?
10. Движение тела с неподвижной осью задано уравнением j = 2p(6t – 3t2) (j – в рад, t – в с). Начало движения при t = 0. Сколько оборотов сделает тело до момента изменения направления вращения?
11. Стержень длиной l упирается верхним концом в стену, а нижним – в пол. Конец, упирающийся в стену, равномерно опускается вниз. Будет ли движение другого конца равномерным?

12. У подножия горы санкам сообщена некоторая скорость, в результате чего санки въезжают на гору и, достигнув точки А начинают скользить обратно. Как направлены нормальное и тангенциальное ускорения в точке А.

13. Тело скользит без трения по вогнутой поверхности. Как в наинизшей точке направлены нормальное и тангенциальное ускорения.
4.
Пусть некоторая точка движется по
окружности радиуса r.
Изменение положения точки в пространстве
за промежуток времени Dt определяется
углом поворота ![]() (рис.
3). Элементарный поворот на угол
можно
рассматривать как вектор
(рис.
3). Элементарный поворот на угол
можно
рассматривать как вектор ![]() . Модуль
вектора
равен
углу поворота, а его направление совпадает
с направлением поступательного движения
острия правого винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняетсяправилу
правого винта.
. Модуль
вектора
равен
углу поворота, а его направление совпадает
с направлением поступательного движения
острия правого винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняетсяправилу
правого винта.
|
|
|
|
Рис. 3
Угловой
скоростью ![]() называется
векторная величина, равная пределу
отношения угла поворота
называется
векторная величина, равная пределу
отношения угла поворота ![]() к
промежутку времени Dt,
за который этот поворот произошел, при
стремлении Dt к
нулю:
к
промежутку времени Dt,
за который этот поворот произошел, при
стремлении Dt к
нулю:
 ,
,
где ![]() –
первая производная от функции угла
поворота
–
первая производная от функции угла
поворота ![]() радиус-вектора
радиус-вектора ![]() по
времениt.
Эту производную принято обозначать,
как
по
времениt.
Эту производную принято обозначать,
как ![]() .
.
Вектор направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым
ускорением ![]() называется
векторная величина, равная пределу
отношения изменения угловой скорости
называется
векторная величина, равная пределу
отношения изменения угловой скорости ![]() к
промежутку времени Dt,
за который это изменение произошло, при
стремлении Dt к
нулю:
к
промежутку времени Dt,
за который это изменение произошло, при
стремлении Dt к
нулю:
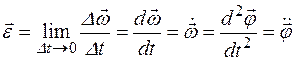 ,
,
где ![]() –
первая производная от функции
–
первая производная от функции ![]() по
времениt,
по
времениt,
![]() –
вторая
производная от функции
по
времениt.
–
вторая
производная от функции
по
времениt.
Эти
производные принято обозначать
соответственно в виде: ![]() и
и ![]() .
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора совпадает с направлением вектора угловой скорости , а при замедленном – противоположно ему.
Кинематические
параметры поступательного и вращательного
движения связаны между собой. Связь
скорости ![]() и
угловой скорости
и
угловой скорости ![]() (см.
рис. 3) определяется следующим образом:
(см.
рис. 3) определяется следующим образом: ![]() .
.
В
векторном виде эту связь для
векторов ![]() и
можно
записать с помощью векторного
произведения:
и
можно
записать с помощью векторного
произведения: ![]() .
.
Ускорение а также
можно выразить через угловые параметры,
разложив ускорение а на
две составляющие ![]() и
и ![]() ,
то есть:
,
то есть: ![]() .
.
Тангенциальная
составляющая
выражается
через угловое ускорение ![]() :
:
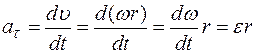 ,
,
а нормальная составляющая – через угловую скорость :
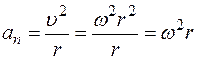 .
.
Тогда
ускорение: ![]() .
.
При равномерном вращении угловая скорость не изменяется. В этом случае вращение можно характеризовать периодом вращенияT , то есть временем, за которое точка совершает один полный оборот.
Угловая скорость равномерного вращения связана с периодом вращения:
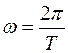 .
.
Частотой вращенияn называется число полных оборотов, совершаемых телом в единицу времени. При равномерном вращении:
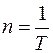 ,
откуда
,
откуда ![]() .
.
5. Рассмотрим движение материальной точки по окружности. Положение точки М на окружности можно задать угловой координатой – углом a, который образует радиус – вектор ОМ с каким - либо неизменным направлением, например, с осью ОХ (рис. 1.1).
Производная угловой координаты a по времени
![]() (1.4)
(1.4)
называется
угловой скоростью.
Вращение называется равномерным, если
угловая скорость постоянна, w=const. Величина
n = ![]() называется частотой
обращения.
Величина Т =1/n
называется периодом
вращения.
называется частотой
обращения.
Величина Т =1/n
называется периодом
вращения.

Рис. 1.1
Первая
производная угловой скорости w по
времени или
вторая производная угловой координаты ![]() по
времени называется угловым
ускорением:
по
времени называется угловым
ускорением:
 .
(1.5)
.
(1.5)
Если
через S обозначить
длину дуги окружности ХМ,
то ее производные V
= dS/dt и ![]() дают
линейную скорость и линейное ускорение
при движении точки по окружности.
Если r –
радиус окружности, то S
= ra.
Дифференцируя это соотношение по
времени, находим
дают
линейную скорость и линейное ускорение
при движении точки по окружности.
Если r –
радиус окружности, то S
= ra.
Дифференцируя это соотношение по
времени, находим
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
6. Первый закон Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью. Если на тело действует неуравновешенная система сил, то инертность сказывается в том, что изменение состояния покоя или движения тела происходит постепенно, а не мгновенно. При этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела при поступательном движении является масса.
Первый закон Ньютона выполняется не во всякой системе отсчета. Системы, в которых он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, является неинерциальной, и в ней не выполняются ни закон инерции, ни второй закон Ньютона, ни закон сохранения импульса.
Понятие «инерциальная система отсчета» является научной абстракцией. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля и т.п.), по отношению к которому и изучается движение тех или иных объектов. Однако в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звездам), поэтому любая реальная система отсчета может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему с началом координат в центре Солнца и с осями, направленными на три звезды. Для решения большинства технических задач инерциальной системой можно считать систему отсчета, жестко связанную с Землей (не учитывается вращение Земли вокруг собственной оси и вокруг Солнца).
Как уже отмечалось, масса – это физическая величина, определяющая инерционные свойства материи. Масса – это свойство самого тела и, в отличие от веса, не зависит от места ее измерения (вес Р тела в разных точках земного шара различен: он максимален на полюсах и минимален на экваторе). Ускорение свободного падения g тел на Землю также зависит от географической широты места наблюдения и от его высоты над уровнем моря. Однако отношение веса тела Р к его ускорению g одинаково во всех точках земного шара. Это отношение и принято для количественного измерения массы:
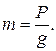 (2.1)
(2.1)
За
единицу массы принят килограмм массы,
равный массе эталона, сделанного из
сплава иридия и платины. Следует отметить,
что масса тела считается постоянной
величиной только в классической механике
Ньютона, изучающей движение тел со
скоростями, небольшими по сравнению со
скоростью света (![]() ).
В современной физике установлено, что
масса тела увеличивается с увеличением
скорости его движения по закону:
).
В современной физике установлено, что
масса тела увеличивается с увеличением
скорости его движения по закону:

где m –
масса тела, движущегося со скоростью ![]() ; с –
скорость света; m0 –
масса покоящегося тела.
; с –
скорость света; m0 –
масса покоящегося тела.
Из формулы (2.1) следует, что вес тела
![]() ,
(2.2)
,
(2.2)
т.е. вес – это сила, с которой тело притягивается Землей, т.е. та сила, которая сообщает телу ускорение g=9,81 м/с2:
1 кГ=1 кг·9,81 м/с2 .
С другой стороны,
1 Н=1 кг·1 м/с2 ,
следовательно,
1 кГ=9,81 Н.
Для описания воздействий тел (материальных точек) друг на друга вводится понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Таким образом, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением (модулем), направлением в пространстве и точкой приложения.
Пример. Какого веса балласт Fx надо сбросить с равномерно спускающегося аэростата, чтобы он начал подниматься с той же скоростью? Вес аэростата с балластом Р=1600 кГ, подъемная сила аэростата F1=1200 кГ. Силу сопротивления воздуха F2 считать одинаковой при подъеме и при спуске.
7. Массой тела называют физическую величину, являющуюся мерой его инерционных свойств.
Свойство тела сохранять свое состояние неизменным называют инерцией, а системы отсчета, в которых выполняется этот закон, - инерциальными.
Определение 2.
Причина изменения состояния тела, т.е. появление ускорения связана с введением понятия силы.
Определение 3.
Силой называют количественную меру простого воздействия на тело со стороны других тел, во время действия которого тело или его части получают ускорения.
В международной системе единиц СИ силу измеряют в Ньютонах ( Н ).
Однако существуют метрические внесистемные единицы: грамм, килограмм и тонна. Эти единицы используются при определении веса тела.
На практике для измерения величины силы используют динамометр - тарированную (градуированную) пружину, снабженную шкалой.
Второй закон Ньютона – дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта.
 Формулировка:
Формулировка:
Ускорение, приобретаемое материальной точкой в инерциальной системе отсчета: - прямо пропорционально действующей на точку (равнодействующей) силе; - обратно пропорционально массе точки; и - направлено в сторону действия силы.
 , (1)
, (1)
Ускорение – вектор, масса – величина скалярная (число), поэтому сила тоже есть вектор, направление которого совпадает с направлением ускорения. Уравнение (1) представляет одну из форм записи второго закона Ньютона.
В механике это уравнение принято называть уравнением движения.
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
Определение 1.
Импульсом
называется величина![]() , где
, где ![]() скорость
тела.
скорость
тела.
В ньютоновской механике предполагается, что масса тела постоянна и не зависит от скорости, поэтому левую часть уравнения (1) можно переписать в виде:
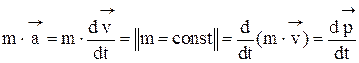 .
( 2 )
.
( 2 )
С учетом ( 2 ) уравнение ( 1 ) принимает вид:
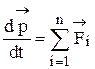 .
( 3 )
.
( 3 )
8.
Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примеразамкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой  , а второе — на первое с силой
. Как соотносятся силы? Третий законНьютона утверждает: сила действия равна по модулю и противоположна по направлению силепротиводействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
, а второе — на первое с силой
. Как соотносятся силы? Третий законНьютона утверждает: сила действия равна по модулю и противоположна по направлению силепротиводействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Современная формулировка
-
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковуюприроду, направленными вдоль прямой, соединяющей эти точки, равными по модулю ипротивоположными по направлению:
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.
Историческая формулировка
-
Действию всегда есть равное и противоположное противодействие, иначе, взаимодействиядвух тел друг на друга равны и направлены в противоположные стороны.
Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как законсохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить егосправедливость[2].
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает законсохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел толькоот модуля разности координат этих тел , то возникает закон сохранения суммарноймеханической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движениямеханических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, законвсемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.
9. Закон гравитационного взаимодействия тел в классической механике носит название закона всемирного тяготения. Этот закон был установлен И.Ньютоном на основе анализа законов движения планет Солнечной системы, открытых И.Кеплером. Согласно этому закону, все тела в природе взаимно притягивают друг друга с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
 (47)
(47)
где
G – коэффициент пропорциональности,
называемый гравитационной постоянной.
Направлена сила вдоль прямой, проходящей
через взаимодействующие тела (рис. 17).
Формула (47) дает численное значение
равных по величине и противоположно
направленных ..
 .
.
Тела, о которых идет речь в соотношении (47), представляют собой, очевидно, материальные точки. Для определения силы взаимодействия тел, которые не могут рассматриваться как материальные точки, их нужно разбить на элементарные объемы ΔVi, каждый из которых можно было бы принять за материальную точку. Каждый такой объем будет иметь массу Δmi. Затем, согласно формуле (47), вычисляются силы притяжения, действующие между всеми возможными элементарными массами в обоих телах, и результирующая сила притяжения вычисляется как векторная сумма (суперпозиция) всех элементарных сил. Практически такое суммирование сводится к интегрированию и является очень сложной математической задачей.

Рис. 17.
Гравитационное взаимодействие двух тел (материальных точек)
Коэффициент пропорциональности между силой и ускорением в формуле (31) принимается равным единице. Тем самым определяется единица измерения силы. Коэффициент пропорциональности в формуле (47) уже невозможно приравнять единице, поскольку единицы измерения всех величин уже определены. Поэтому коэффициентом пропорциональности в формуле (47) является не равная единице величина, имеющая размерность и носящая особое название – гравитационная постоянная. Ее значение (с определенной точностью):
G = 6,67545×10−11 м³/(кг·с²). (48)
Ее физический смысл можно сформулировать следующим образом: гравитационная постоянная численно равна силе, с которой притягиваются две материальные точки массой 1 кг, находящиеся на расстоянии 1м друг от друга.
Как видно, гравитационная сила взаимодействия тел весьма мала. Она имеет существенное значение только при очень больших массах взаимодействующих тел.
Величина гравитационной постоянной не зависит от природы взаимодействующих тел, оно одно и то же для всех материальных тел. Ее значение определяется экспериментально. Первый эксперимент по измерению гравитационной постоянной провел Генри Кавендиш в 1798 г. В своем эксперименте он использовал так называемые крутильные весы (рис. 18). Два свинцовых шара m (с массой 729 г каждый), прикрепленных к концам легкого коромысла, помещались вблизи симметрично расположенных шаров М (с массой по 158 кг). Коромысло подвешивалось на упругой нити. Верхний конец нити был закреплен в установочной головке, поворотом которой можно было менять расстояние между шарами m и М. Сила притяжения шаров m и М определялась по углу закручивания нити, поскольку по закону Гука этот угол пропорционален силе упругости, которая уравновешивает силу взаимодействия шаров.

Рис. 18.
Схема опыта Г. Кавендиша
Понятие «масса» фигурирует в двух разных законах – во втором законе Ньютона (31) и в законе всемирного тяготения (47). В первом случае она характеризует инертные свойства тела, во втором – гравитационные свойства, то есть способность тел притягиваться друг к другу. В связи с этим возникает вопрос, не следует ли различать инертную массу min и массу гравитационную (или тяготеющую) mg? Ответ на этот вопрос может дать только опыт.
Еще в XVII в. Г. Галилей экспериментально установил, что в поле тяжести Земли все тела падают с одним и тем же ускорением. Из этого экспериментального факта следует равенство инерционной и гравитационной масс. В самом деле, рассмотрим 2 тела с разными массами. Обозначим инерционную и гравитационную массы этих тел как m1in, m1g, m2in, m2g. Пусть g – ускорение свободного падения, M – масса Земли, R – ее радиус. Тогда можно написать:

Разделив первое уравнение на второе получим:

т. е. инерционные массы пропорциональны гравитационным.
10. Деформация тел — это процесс изменения взаиморасположения молекул какой-либо среды, которое в дальнейшем приводит к видоизменению формы и размеров тела. Типы деформаций: растяжение, сжатие, изгиб, сдвиг, кручение.
Виды деформаций: упругая деформация — это деформация, которая после действия силы, вызвавшей ее, полностью исчезает, при этом тело снова приобретает прежние размеры и форму; пластическая деформация — это деформация, которая после действия силы, вызвавшей ее, не исчезает, а приводит к изменению прежних своих размеров и форм, то есть произошло необратимое изменение в структуре твердого тела.
Величины
для упругих деформаций (сжатие-растяжение):
абсолютное удлинение ![]() —
это есть величина, которая показывает
изменение длины, которое происходит
под действием внешней силы; относительное
удлинение
—
это есть величина, которая показывает
изменение длины, которое происходит
под действием внешней силы; относительное
удлинение ![]() —
это величина, которая характеризует,
какую часть от длины недеформированного
тела составляет изменение длины тела
при деформации, которая определяется
отношением абсолютного удлинения к
длине в недеформированном состоянии и
записывается:
—
это величина, которая характеризует,
какую часть от длины недеформированного
тела составляет изменение длины тела
при деформации, которая определяется
отношением абсолютного удлинения к
длине в недеформированном состоянии и
записывается: ![]()
Причина деформации — это движение.
Сила упругости — это сила, которая возникает при упругих деформациях и действует только в процессе деформации.
Закон
Гука: сила упругости, которая возникает
при упругой деформации, прямо
пропорциональна деформации тела, взятой
со знаком «минус», и записывается
формулой: ![]() ,
где k — жесткость тела или коэффициент
упругости.
,
где k — жесткость тела или коэффициент
упругости.
Коэффициент жесткости — это физическая величина, которая является характеристикой свойств упругих тел.
Жесткость
тела, имеющего цилиндрическую форму,
определяется формулой: ![]()
![]() характеристикой
упругих свойств тела.
характеристикой
упругих свойств тела.
Силы трения. Силы трения — это такие силы, которые возникнут при соприкосновении тел, действующие вдоль соприкасающихся поверхностей, препятствующие их относительному перемещению. Виды трения:
cухое трение:
трение покоя;
трение скольжения;
трение качения.
жидкое (вязкое) трение.
Сухое трение — это трение, возникающее между поверхностями двух твердых тел.
Трение покоя — это трение, возникающее при отсутствии относительного движения соприкасающихся поверхностей.
Формула
для вычисления силы трения покоя: 
Трение скольжения — это трение, возникающее в процессе скольжения одной поверхности по другой. Трение качения — это трение, возникающее между опорой и катящимся по ней телом. Сила трения качения — это сила, которая необходима для равномерного прямолинейного качения тела по горизонтальной плоскости.
Закон
Кулона: модуль
силы трения качения пропорционален
коэффициенту трения качения, модулю
силы реакции опоры и обратно пропорционален
радиусу катящегося тела, и записывается
формулой: ![]()

Момент
трения — это физическая величина,
которую создает пара сил, приложенных
к катящемуся телу: ![]()
Жидкое (вязкое) трение — это трение, возникающее между поверхностью твердого тела и жидкой (газообразной) средой, где движется твердое тело.
Гравитационное взаимодействие — это самое слабое взаимодействие, которое характеризуется своей универсальностью, это взаимодействие присуще всем материальным объектам.
Гравитационная масса — это физическая величина, которая характеризует способность тела участвовать в гравитационном взаимодействии; эта характеристика определяет гравитационные свойства.
Закон всемирного тяготения: две материальные частицы или материальные точки притягиваются друг к другу с силой, которая определяется отношением их масс к квадрату расстояния между ними
Гравитационная
постоянная —
это коэффициент пропорциональности,
который имеет следующее значение: 
Физический смысл гравитационной постоянной: гравитационная постоянная представляет численное значение силы, с которой притягиваются два тела друг к другу, с массами равными по 1 кг, расположенными на расстоянии 1 м друг от друга.
Формула
для гравитационного взаимодействия
тела с Землей: 
Гравитационное поле (поле тяготения) — это поле, где осуществляется тяготение между телами, гравитационное поле является одной из форм материи.
11. Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.Кинетическая энергия механической системы — это энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.Ek=mv2/2/
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и
характером
сил взаимодействия между ними.
Потенциальная энергия тела ![]() в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
![]()
где ![]() —
масса тела,
—
масса тела, ![]() —
ускорение свободного падения,
—
ускорение свободного падения, ![]() —
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
—
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, —консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной; ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
![]()
16) Работа. Механическая работа
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы
В механике можно ввести понятие работы, исходя из довольно простых представлений
12.
лучае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1):
![]()
Единицы измерения работы: 1 Дж (джоуль)= 1 Н-м; 1 кДж (килоджоуль) = 103 Дж.
Рассмотрим частные случаи.
1. Силы, совпадающие с направлением перемещения, называются движущими силами.
Направление вектора силы совпадает с направлением перемещения (рис. 15.2). В этом случае α = 0° (cos α = 1). Тогда W = FS > 0.
2. Силы, перпендикулярные направлению перемещения, работы не производят (рис. 15.3).
Сила F перпендикулярна направлению перемещения, α = 90° (cos α = 0); W = 0.
3. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4).
Сила F направлена в обратную от перемещения S сторону. В этом случае α = 180° (cos α = — 1), следовательно, W = — FS < 0.
Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость.
Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
13. Пусть тело движется под действием некоторой переменной силы F по прямой, причем направление силы совпадает с направлением движения, а работа А, произведенная силой F при перемещении тела из т.х=а по прямой ОХ в точку х=b той же прямой, может быть выражена (в случае когда F=F(x) есть непрерывная функции на [a; b]) с помощью определенного интеграла следующим образом:
![]() .
(1)
.
(1)
Пример 13. Рессора прогибается под нагрузкой 1,5 т на 1 см. Какую работу надо затратить для деформации рессора на 3 см? (Сила деформации пропорциональна величине деформации).
Решение: обозначим через х – величину деформации, т.к. F=kx, где k - коэффициент пропорциональности (коэффициент жесткости).
Известно,
что при х=0,01 м F=1,500 ![]() (Н),
(Н),
то ![]() ,
следовательно,
,
следовательно, ![]() .
.
По
формуле (1) работа ![]()
14.
|
![]() :
: ![]() .
(19.2)
.
(19.2)
![]() .
(19.3)Работа
равнодействующей сил, приложенных к
телу, равна изменению кинетической
энергии тела. Это
утверждение называют теоремой о
кинетической энергии.
.
(19.3)Работа
равнодействующей сил, приложенных к
телу, равна изменению кинетической
энергии тела. Это
утверждение называют теоремой о
кинетической энергии.
Так как изменение кинетической энергии равно работе силы (19.3), кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях.
Если
начальная скорость движения тела
массой ![]() равна
нулю и тело увеличивает свою скорость
до значения
равна
нулю и тело увеличивает свою скорость
до значения ![]() ,
то работа силы равна конечному значению
кинетической энергии тела:
,
то работа силы равна конечному значению
кинетической энергии тела:
![]() .
(19.4)Так как перемещение совпадает по
направлению с вектором силы тяжести,
работа силы тяжести равна
.
(19.4)Так как перемещение совпадает по
направлению с вектором силы тяжести,
работа силы тяжести равна
![]() .
(20.1)что работа
силы тяжести не зависит от траектории
движения тела и всегда равна произведению
модуля силы тяжести на разность высот
в начальном и конечном положениях.При
движении вниз работа силы тяжести
положительна, при движении вверх -
отрицательна. Работа силы тяжести на
замкнутой траектории равна нулю.Значение
потенциальной энергии тела, поднятого
над Землей, зависит от выбора нулевого
уровня, т.е. высоты, на которой потенциальная
энергия принимается равной нулю. Обычно
принимают, что потенциальная энергия
тела на поверхности Земли равна нулю.
.
(20.1)что работа
силы тяжести не зависит от траектории
движения тела и всегда равна произведению
модуля силы тяжести на разность высот
в начальном и конечном положениях.При
движении вниз работа силы тяжести
положительна, при движении вверх -
отрицательна. Работа силы тяжести на
замкнутой траектории равна нулю.Значение
потенциальной энергии тела, поднятого
над Землей, зависит от выбора нулевого
уровня, т.е. высоты, на которой потенциальная
энергия принимается равной нулю. Обычно
принимают, что потенциальная энергия
тела на поверхности Земли равна нулю.
16.Растворы,
осмотическое давление. Влажность:
относительная и абсолютная влажность,
точка росы. Осмотическое
давление (обозначается
π) — избыточное гидростатическое
давление на раствор, отделённый от
чистого растворителя полупроницаемой
мембраной, при котором прекращается
диффузия растворителя через мембрану
(осмос). Это давление стремится уравнять
концентрации обоих растворов вследствие
встречной диффузии молекул растворённого
вещества и растворителя. Величина
осмотического давления, создаваемая
раствором, зависит от количества, а не
от химической природы растворенных в
нём веществ (илиионов, если молекулы
вещества диссоциируют), следовательно,
осмотическое давление является
коллигативным свойством раствора. Чем
больше концентрация вещества в растворе,
тем больше создаваемое им осмотическое
давление. Это правило, носящее название
закона осмотического давления, выражается
простой формулой, очень похожей на некий
закон идеального газа: ![]() ,где
i — изотонический коэффициент раствора;
C — молярная концентрация раствора,
выраженная через комбинацию основных
единиц СИ, то есть, в моль/м3,
а не в привычных моль/л; R — универсальная
газовая постоянная; T — термодинамическая
температура раствора. Абсолютная
влажность воздуха (f) —
это количество водяного пара, фактически
содержащегося в 1м3 воздуха: f =
m (масса содержащегося в воздухе водяного
пара)/ V (объём влажного воздуха). Обычно
используемая единица абсолютной
влажности: (f) =
г/ Относительная влажность: φ = (абсолютная
влажность)/(максимальная влажность).
Относительная влажность обычно выражается
в процентах. Эти величины связаны между
собой следующим отношением: φ =
(f×100)/fmax. Точка росы — это температура,
до которой должен охладиться воздух,
чтобы содержащийся в нём пар достиг
состояния насыщения и начал конденсироваться
в росу.
,где
i — изотонический коэффициент раствора;
C — молярная концентрация раствора,
выраженная через комбинацию основных
единиц СИ, то есть, в моль/м3,
а не в привычных моль/л; R — универсальная
газовая постоянная; T — термодинамическая
температура раствора. Абсолютная
влажность воздуха (f) —
это количество водяного пара, фактически
содержащегося в 1м3 воздуха: f =
m (масса содержащегося в воздухе водяного
пара)/ V (объём влажного воздуха). Обычно
используемая единица абсолютной
влажности: (f) =
г/ Относительная влажность: φ = (абсолютная
влажность)/(максимальная влажность).
Относительная влажность обычно выражается
в процентах. Эти величины связаны между
собой следующим отношением: φ =
(f×100)/fmax. Точка росы — это температура,
до которой должен охладиться воздух,
чтобы содержащийся в нём пар достиг
состояния насыщения и начал конденсироваться
в росу.
17.Кристаллические и аморфные твердые тела. Жидкие кристаллы. Деформация твердых тел. Виды деформации. Твердое тело— агрегатное состояние вещества, характеризующееся постоянством формы и характером движения атомов, которые совершают малые колебания около положений равновесия. Кристаллические тела. Твердое тело в обычных условиях трудно сжать или растянуть. Для придания твердым телам нужной формы или объема на заводах и фабриках их обрабатывают на специальных станках: токарных, строгальных, шлифовальных. Аморфные тела. Кроме кристаллических, к твердым телам относят также аморфные тела. АТ — это твердые тела, для которых характерно неупорядоченное расположение частиц в пространстве. К аморфным телам относятся стекло, янтарь, различные другие смолы, пластмассы. Хотя при комнатной температуре эти тела сохраняют свою форму, но при повышении температуры они постепенно размягчаются и начинают течь, как жидкости: у аморфных тел нет определенной температуры, плавления. Жидкие кристаллы - Это фазовое состояние, в которое переходят некоторые вещества при определенных условиях (температура, давление, концентрация в растворе). ЖК обладают одновременно свойствами как жидкостей (текучесть), так и кристаллов (анизотропия).Деформация твердого тела-Изменение линейных размеров или форм твердого тела под действием внешних сил. Виды деформаций: Деформация растяжения или сжатия - изменение любого линейного размера тела (длины, ширины или высоты). Деформация сдвига - перемещение всех слоев твердого тела в одном направлении параллельно некоторой плоскости сдвига. Деформация изгиба - сжатие одних частей тела при растяжении других. Деформация кручения - поворот параллельных сечений образца вокруг некоторой оси под действием внешней силы.
18.Механические
свойства твердых тел. Закон Гука. Кривая
деформации. Пределы упругости и прочности.
Пластическая деформация.Под
действием приложенных внешних сил
твердые тела изменяют свою форму и объем
- деформируются. Если после прекращения
действия силы, форма и объем тела
полностью восстанавливаются, то
деформацию называют упругой,
а тело - абсолютно упругим. Деформации,
которые не исчезают после прекращения
действия сил, называются пластическими,
а тела - пластичными.Различают следующие
виды деформаций: растяжение, сжатие,
сдвиг, кручение и изгиб.Деформацию
растяжения характеризуют абсолютным
удлинением дельта l и
относительным удлинением е: ![]() где l0-
начальная длина, l-
конечная длина стержня. Механическим
напряжением называют отношение модуля
силы упругости F к площади поперечного
сечения тела S:б=F/S.
где l0-
начальная длина, l-
конечная длина стержня. Механическим
напряжением называют отношение модуля
силы упругости F к площади поперечного
сечения тела S:б=F/S.
В СИ за единицу механического напряжения принимают 1Па = 1Н/м2.Закон Гука: при малых деформациях напряжение прямо пропорционально относительному удлинению (б = Е • е). Упругой деформацией называется такая, при которой после прекращения действия силы тело восстанавливает свои первоначальные форму и размеры. Пластической деформацией назыв. такая, при которой после прекращения действия нагрузки тело не восстанавливает своей первоначальной формы и размеров. Пластической деформации всегда предшествует упругая.
20.Основное
уравнение молекулярно-кинетической
теории газов.
Для объяснения свойств вещества в
газообразном состоянии используется
модель идеального газа. В модели
идеального газа предполагается следующее:
молекулы обладают пренебрежимо малым
объемом по сравнению с объемом сосуда,
между молекулами не действуют силы
притяжения, при соударениях молекул
друг с другом и со стенками сосуда
действуют силы отталкивания. Давление
идеального газа. Одним из первых и важных
успехов молекулярно-кинетической теории
было качественное и количественное
объяснение явления давления газа на
стенки сосуда. Качественное объяснение
давления со стенками сосуда взаимодействуют
с ними по законам механики как упругие
тела. При столкновении молекулы со
стенкой сосуда проекция ![]() вектора
скорости на ось ОХ, перпендикулярную
стенке, изменяет свой знак на
противоположный, но остается постоянной
по модулю
вектора
скорости на ось ОХ, перпендикулярную
стенке, изменяет свой знак на
противоположный, но остается постоянной
по модулю

Поэтому
в результате столкновения молекулы со
стенкой проекция ее импульса на ось ОХ
изменяется от ![]() до
до ![]() .
Изменение импульса молекулы показывает,
что на нее при столкновении действует
сила
.
Изменение импульса молекулы показывает,
что на нее при столкновении действует
сила ![]() ,
направленная от стенки. Изменение
импульса молекулы равно импульсу
силы
:
,
направленная от стенки. Изменение
импульса молекулы равно импульсу
силы
: ![]() Во
время столкновения молекула действует
на стенку с силой
Во
время столкновения молекула действует
на стенку с силой ![]() ,
равной по третьему закону Ньютона
силе
по
модулю и направленной противоположно.
Молекул газа очень много, и удары их о
стенку следуют один за другим с очень
большой частотой. Среднее значение
геометрической суммы сил, действующих
со стороны отдельных молекул при их
столкновениях со стенкой сосуда, и
является силой давления газа. Давление
газа равно отношению модуля силы
давления
,
равной по третьему закону Ньютона
силе
по
модулю и направленной противоположно.
Молекул газа очень много, и удары их о
стенку следуют один за другим с очень
большой частотой. Среднее значение
геометрической суммы сил, действующих
со стороны отдельных молекул при их
столкновениях со стенкой сосуда, и
является силой давления газа. Давление
газа равно отношению модуля силы
давления ![]() к
площади стенки S:
к
площади стенки S: ![]() На
основе использования основных положений
молекулярно-кинетической теории было
получено уравнение, которое позволяло
вычислить давление газа, если известны
масса m0 молекулы газа, среднее значение
квадрата скорости молекул
На
основе использования основных положений
молекулярно-кинетической теории было
получено уравнение, которое позволяло
вычислить давление газа, если известны
масса m0 молекулы газа, среднее значение
квадрата скорости молекул ![]() и
концентрация n молекул:
и
концентрация n молекул: ![]() -это
уравнение называют основным уравнением
молекулярно-кинетической теории.
Обозначив среднее значение кинетической
энергии поступательного движения
молекул идеального газа
-это
уравнение называют основным уравнением
молекулярно-кинетической теории.
Обозначив среднее значение кинетической
энергии поступательного движения
молекул идеального газа ![]() :
: ![]() получим
получим ![]() .
Давление идеального газа равно двум
третям средней кинетической энергии
поступательного движения молекул,
содержащихся в единице объема.
.
Давление идеального газа равно двум
третям средней кинетической энергии
поступательного движения молекул,
содержащихся в единице объема.
21.Внутренняя
энергия системы как функция состояния.
Эквивалентность теплоты и работы. Первое
начало термодинамики. Внутренняя
энергия -
термодинамическая функция состояния
системы, ее энергия, определяемая
внутренним состоянием. Она складывается
в основном из кинетической энергии
движения частиц (атомов, молекул,
ионов, электронов)
и энергии взаимодействия между ними
(внутри- и межмолекулярной). На внутреннюю
энергию влияет изменение внутреннего
состояния системы под действием внешнего
поля; во внутреннюю энергию входит, в
частности, энергия, связанная с
поляризацией диэлектрика во внешнем
электрическом поле и намагничиванием
парамагнетика во внешнем магнитном
поле. Кинетическая энергия системы как
целого и потенциальная энергия,
обусловленная пространственным
расположением системы, во внутреннюю
энергию не включаются. В термодинамике
определяется лишь изменение внутренней
энергии в различных процессах. Поэтому
внутреннюю энергию задают с точностью
до некоторого постоянного слагаемого,
зависящего от энергии, принятой за нуль
отсчета. Внутренняя энергия U как
функция состояния вводится первым
началом термодинамики, согласно которому
разность между теплотой Q, переданной
системе, и работой W,
совершаемой системой, зависит только
от начального и конечного состояний
системы и не зависит от пути перехода,
т.е. представляет изменение функции
состояния ΔU ![]() где
U1 и U2 -
внутренняя энергия системы в начальном
и конечном состояниях соответственно.
Уравнение (1) выражает закон сохранения
энергии в применении к термодинамическим
процессам, т.е. процессам, в которых
происходит передача теплоты. Для
циклического процесса, возвращающего
систему в начальное состояние, ΔU=0.
В изохорных процессах, т.е. процессах
при постоянном объеме, система не
совершает работы за счет расширения, W=0
и теплота, переданная системе, равна
приращению внутренней энергии: Qv=ΔU.
Для адиабатических процессов, когда Q=0,
ΔU=-W. Внутренняя
энергия системы
как функция ее энтропии S, объема V и
числа молей mi i-того
компонента представляет собой
термодинамический потенциал. Это
является следствием первого и второго
начал термодинамики и выражается
соотношением:
где
U1 и U2 -
внутренняя энергия системы в начальном
и конечном состояниях соответственно.
Уравнение (1) выражает закон сохранения
энергии в применении к термодинамическим
процессам, т.е. процессам, в которых
происходит передача теплоты. Для
циклического процесса, возвращающего
систему в начальное состояние, ΔU=0.
В изохорных процессах, т.е. процессах
при постоянном объеме, система не
совершает работы за счет расширения, W=0
и теплота, переданная системе, равна
приращению внутренней энергии: Qv=ΔU.
Для адиабатических процессов, когда Q=0,
ΔU=-W. Внутренняя
энергия системы
как функция ее энтропии S, объема V и
числа молей mi i-того
компонента представляет собой
термодинамический потенциал. Это
является следствием первого и второго
начал термодинамики и выражается
соотношением: ![]()
относительная
диэлектрическая проницаемость.
Электрическая постоянная. Напряженность
электрического поля. Диэлектри́ческая
проница́емость среды
— физическая величина, характеризующая
свойства изолирующей (диэлектрической)
среды и показывающая зависимость
электрической индукции от напряжённости
электрического поля. Относительная
диэлектрическая проницаемость ε является
безразмерной и показывает, во сколько
раз сила взаимодействия двух электрических
зарядов в среде меньше, чем в вакууме.
Эта величина для воздуха и большинства
других газов в нормальных условиях
близка к единице (в силу их низкой
плотности). Для большинства твёрдых или
жидких диэлектриков относительная
диэлектрическая проницаемость лежит
в диапазоне от 2 до 8 (для статического
поля). Диэлектрическая постоянная воды
в статическом поле достаточно высока
— около 80. Электрическая постоянная
(e0)
-физ постоянная, входящая в ур-ния законов
электрич. поля (напр., в Кулона
закон )при
записи этих ур-ний в рационализованной
форме, в соответствии с к-рой образованы
электрич. и магн. единицы Международной
системы единиц; по
старой терминологии Э. п. называется
диэлектрич. проницаемостью вакуума. ![]()
![]() где
m0 - магнитная
постоянная. В
отличие от диэлектрич. проницаемости
e, зависящей от типа вещества, темп-ры,
давления и др. параметров, Э. п. e0 зависит
только от выбора системы единиц. Напр.,
в гауссовой СГС
системе единиц
где
m0 - магнитная
постоянная. В
отличие от диэлектрич. проницаемости
e, зависящей от типа вещества, темп-ры,
давления и др. параметров, Э. п. e0 зависит
только от выбора системы единиц. Напр.,
в гауссовой СГС
системе единиц![]() напряженность
электрического поля в
классической электродинамике (E)
- векторная характеристика электрич.
поля, сила, действующая па покоящийся
в данной системе отсчёта единичный
олектрич. заряд. При этом предполагается,
что внесение заряда (заряженного пробного
тела) во внеш. поле E не
изменяет такового. Иногда вместо H. э.
п. говорят просто "электрич. поле".
Размерность Н. э. п. в гауссовой системе
- L-1/2M1/2T -1,
в СИ - LMT-3I-1;
единицей H. э. п. в СИ является вольт на
метр (1 СГСЭ = 3.104 В/м).
Распределение H. э. п. в пространстве
обычно характеризуют с помощью семейства
линий E (силовых
линий электрич. поля), касательные к
к-рьш в каждой точке совпадают с
направлениями вектора E.
Как и любое векторное поле, поле E разбивается
на две составляющие: потенциальную
([
напряженность
электрического поля в
классической электродинамике (E)
- векторная характеристика электрич.
поля, сила, действующая па покоящийся
в данной системе отсчёта единичный
олектрич. заряд. При этом предполагается,
что внесение заряда (заряженного пробного
тела) во внеш. поле E не
изменяет такового. Иногда вместо H. э.
п. говорят просто "электрич. поле".
Размерность Н. э. п. в гауссовой системе
- L-1/2M1/2T -1,
в СИ - LMT-3I-1;
единицей H. э. п. в СИ является вольт на
метр (1 СГСЭ = 3.104 В/м).
Распределение H. э. п. в пространстве
обычно характеризуют с помощью семейства
линий E (силовых
линий электрич. поля), касательные к
к-рьш в каждой точке совпадают с
направлениями вектора E.
Как и любое векторное поле, поле E разбивается
на две составляющие: потенциальную
([ ![]() E п)
= 0, E п =
-
E п)
= 0, E п =
- ![]() j е )и
вихревую (
j е )и
вихревую ( ![]() ЕB =
0, ЕB =
[
ЕB =
0, ЕB =
[ ![]() Am]).
В частности, электрич. поле, создаваемое
системой неподвижных зарядов, является
чисто потенциальным. Электрич. поле
излучения, в т. ч. поле E в
поперечных эл.-магп. волнах, является
чисто вихревым. Вместе с вектором магн.
индукции В H.
э. п. составляет единый 4-тензор
электромагнитного поля. Поэтому чисто
олектрич. поле данной системы зарядов
существует лишь в "избранной"
системе отсчёта, где заряды неподвижны.
В др. инерцпальных системах отсчёта,
перемещающихся относительно "избранной"
с пост. скоростью u,
возникает ещё имагнитное поле В'
= = [uE]/
Am]).
В частности, электрич. поле, создаваемое
системой неподвижных зарядов, является
чисто потенциальным. Электрич. поле
излучения, в т. ч. поле E в
поперечных эл.-магп. волнах, является
чисто вихревым. Вместе с вектором магн.
индукции В H.
э. п. составляет единый 4-тензор
электромагнитного поля. Поэтому чисто
олектрич. поле данной системы зарядов
существует лишь в "избранной"
системе отсчёта, где заряды неподвижны.
В др. инерцпальных системах отсчёта,
перемещающихся относительно "избранной"
с пост. скоростью u,
возникает ещё имагнитное поле В'
= = [uE]/ ![]() ,
обусловленное появлением конвекц.
токов j =
ru/
,
обусловленное появлением конвекц.
токов j =
ru/ ![]() (r
- плотность заряда в "избранной"
системе).
(r
- плотность заряда в "избранной"
системе).
15. Материя — объективная реальность, данная нам В ОЩУЩЕНИЯХ….
Материя несотворима, неуничтожима, вечна и бесконечна.
Типы материальных систем, известные современной науке:
1) элементарные частицы
2) поля
3) атомы
4) молекулы
5) макроскопические тела
6) геологические системы
7) и т.д.
Этим и другим материальным системам соответствуют структурные уровни организации материи (материя структурирована и систематизирована)
Атрибут — неотъемлемое свойство материи.
1) Структурность материи проявляется в существовании бесконечно многообразных материальных образований, каждое из которых представляет собой специфические единичные вещь, процесс, которые локализованы в пространстве и времени: Вселенная, галактика, звезда, планета, молекула, атом, элементарная частица и др. Вместе с тем они тесно взаимосвязаны между собой, так как одни материальные образования являются составными частями других, то есть входят в их структуру в качестве элементов.
2) Системность материи появляется во взаимосвязи вещей и процессов, в регулярном пересечении структурных уровней организации материального мира, в постоянном нарушении автономии, «параллелизма» микро- , макро- и мегамиров, живого и неживого. Основная проблема здесь заключается в нерешенности вопроса перехода от неживой природы к живой в едином эволюционном процессе.
Материя — это все то, что прямо или косвенно действует на органы чувств человека и другие объекты. Окружающий нас мир, все существующее вокруг нас представляет собой материю. Неотъемлемое свойство материи — движение.
Движение материи — любые изменения, происходящие с материальными объектами в результате их взаимодействия.
Материя не существует в бесформенном состоянии, из нее образуется сложная иерархическая система материальных объектов различных масштабов и сложностей.
Для естествоиспытателей представляет интерес не материя или движение вообще, а конкретные виды материи и движения.
В современном естествознании различают 3 вида материи:
1. Вещество — основной вид материи, обладающий массой. К вещественным объектам относятся элементарные частицы, атомы, молекулы, многочисленные образовавшиеся из них материальные объекты. В химии вещества подразделяются на простые (с атомами одного химического элемента) и сложные (химические соединения). свойства вещества зависят от внешних условий и интенсивности взаимодействия атомов и молекул. Это и обуславливает различные агрегатные состояния вещества (твердое, жидкое, газообразное + плазма при сравнительно высокой температуре) переход вещества из одного состояния в другое можно рассмотреть как один из видов движения материи.
|
|
|
2. Физическое поле — особый вид материи, который обеспечивает физическое взаимодействие материальных объектов и систем.
Физические поля:
· Электромагнитное и гравитационное
· Поле ядерных сил
· Волновые (квантовые) поля
Источник физических полей — элементарные частицы. Направление для электромагнитного поля — источник, заряженные частицы
Физические поля, которые создаются частицами переносят взаимодействие между этими частицами с конечной скоростью.
Квантовые теории — взаимодействие обусловлено обменом квантами поля между частицами.
3. Физический вакуум — низшее энергетическое состояние квантового поля. Этот термин введен в квантовой теории поля для объяснения некоторых микропроцессов.
Среднее число частиц (квантов поля) вакууме равно нулю, однако в нем могут рождаться виртуальные частицы, то есть частицы в промежуточном состоянии, существующие короткое время. Виртуальные частицы влияют на физические процессы.
Принято считать, что не только вещество, но и поле и вакуум имеют дискретную структуру. Согласно квантовой теории поле, пространство и время в очень малых масштабах образуют пространственно-временную среду с ячейками. Квантовые ячейки настолько малы (10-35—10-33 ), что их можно не учитывать при описании свойств электромагнитных частиц, считая пространство и время непрерывными.
Вещество воспринимается как непрерывная сплошная среда. для анализа и описания свойств такого вещества в большинстве случаев учитывается только его непрерывность. Однако, то же вещество при объяснении тепловых явлений, химических связей, электромагнитных излучений рассматривается как дискретная среда, которая состоит из взаимодействующих между собой атомов и молекул.
Дискретность и непрерывность присущи физическому полю, но при решении многих физических задач принято считать гравитационное, электромагнитное и другие поля непрерывными. Однако в квантовой теории поля предполагается, что физические поля дискретны, следовательно, для одних и тех же видов материи характерна прерывность и непрерывность.
Для классического описания природных явлений достаточно учитывать непрерывные свойства материи, а для характеристики различных микропроцессов — дискретные.
Непрерывность и дискретность — неотъемлемые свойства материи.
16.
Потенциальная
энергия системы во внешнем поле.
Предположим,
что механическая система, состоящая из
n частиц, находится во внешнем потенциальном
поле. Определим работу, которую совершают
внешние консервативные силы на перемещение
механической системы за элементарный
промежуток времени.
Как убедились,
любая частица в потенциальном поле
наделена потенциальной энергией.
Обозначим потенциальные энергии частиц
механической системы как ![]() ,
где
,
где ![]() радиус-векторы,
характеризующие положения частиц.
Покажем,
что потенциальная энергия системы во
внешнем потенциальном поле есть сумма
потенциальных энергий составляющих
систему частиц:
радиус-векторы,
характеризующие положения частиц.
Покажем,
что потенциальная энергия системы во
внешнем потенциальном поле есть сумма
потенциальных энергий составляющих
систему частиц:
![]() Пусть
частицы системы за элементарный
промежуток времени dt совершили
перемещения
Пусть
частицы системы за элементарный
промежуток времени dt совершили
перемещения ![]() .
Согласно результату, полученному выше,
работа сил поля на перемещение любой
частицы равна убыли потенциальной
энергии этой частицы:
.
Согласно результату, полученному выше,
работа сил поля на перемещение любой
частицы равна убыли потенциальной
энергии этой частицы:
![]() Суммируя
эти элементарные работы, получим полную
работу внешних консервативных сил на
перемещение системы за время dt:
Суммируя
эти элементарные работы, получим полную
работу внешних консервативных сил на
перемещение системы за время dt:
![]() .
Это
доказывает утверждение (6.34): работа
внешних консервативных сил равна убыли
потенциальной энергии системы в силовом
поле:
.
Это
доказывает утверждение (6.34): работа
внешних консервативных сил равна убыли
потенциальной энергии системы в силовом
поле:
![]()
Градиент скалярной функции – это вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.
![]()
Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала φ постоянного во времени поля равен:
![]()
где ![]() –
нормаль к эквипотенциальной поверхности
в данной точке поля.
–
нормаль к эквипотенциальной поверхности
в данной точке поля.
Градиент
скалярного потенциала φ в каждой точке
совпадает с касательной к силовой линии
напряженности электрического поля ![]() в
данной точке и имеет направление,
противоположное вектору
в
данной точке и имеет направление,
противоположное вектору
Потенциальная
энергия ![]() —
скалярная физическая величина,
представляющая собой часть полной
механической энергии системы, находящейся
в полеконсервативных сил. Зависит от
положения материальных точек, составляющих
систему, и характеризует работу,
совершаемую полем при их перемещении.
Термин «потенциальная энергия» был
введен в XIX веке шотландским инженером
и физиком Уильямом Ренкином.
—
скалярная физическая величина,
представляющая собой часть полной
механической энергии системы, находящейся
в полеконсервативных сил. Зависит от
положения материальных точек, составляющих
систему, и характеризует работу,
совершаемую полем при их перемещении.
Термин «потенциальная энергия» был
введен в XIX веке шотландским инженером
и физиком Уильямом Ренкином.
Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.
Потенциальная
энергия тела ![]() в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
![]()
где ![]() —
масса тела,
—
масса тела, ![]() —
ускорение свободного падения,
—
ускорение свободного падения, ![]() —
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
—
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
17. Если на материальную точку действует сила вида
![]() ,
(8)
,
(8)
то говорят, что материальная точка находится в поле центральных сил, если начало координат совпадает с центром сил.
Примерами материальных точек в таком поле являются искусственные спутники Земли.
Очевидно,
что момент ![]() центральных
сил
центральных
сил ![]() относительно
центра сил 0 равен нулю. Следовательно,
при движении в центральном поле момент
импульса материальной точки остается
постоянным.
относительно
центра сил 0 равен нулю. Следовательно,
при движении в центральном поле момент
импульса материальной точки остается
постоянным.
Вектор ![]() всегда
ортогонален плоскости векторов
всегда
ортогонален плоскости векторов ![]() и
и ![]() .
Поэтому постоянство направления
свидетельствует
о том, что движение материальной точки
в поле центральных сил происходит в
одной плоскости.
.
Поэтому постоянство направления
свидетельствует
о том, что движение материальной точки
в поле центральных сил происходит в
одной плоскости.
Материальная точка, движущаяся в поле центральных сил, представляет собой консервативную систему. Поэтому при движении материальной точки сохраняется и полная механическая энергия точки, т. е.
![]() .
(9)
.
(9)
Для гравитационного центрального поля большой массы М имеем
![]() .
(10)
.
(10)
В этом случае траекторией материальной точки является эллипс, один из фокусов которого совпадает с центром силы, т. е. с положением центра массы М. При E = 0 траекторией частицы является парабола, а при Е > О – гипербола.
18.
Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
![]()
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.
![]()
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Так же есть:
Потенциальная
энергия : ![]()
Кинетическая
энергия ![]()
Тут мы использовали :
![]() —
Потенциальная
энергия упруго деформированного тела
—
Потенциальная
энергия упруго деформированного тела
![]() —
Коэффициент
упругости пружины
—
Коэффициент
упругости пружины
![]() —
Деформация
пружины
—
Деформация
пружины