Построение линейного систематического кода
Для этого используется образующая матрица Pn,k, состящая из двух матриц Uk – информационной, квадратной kk, и Hρ – проверочной, kρ:
P
n,k
=
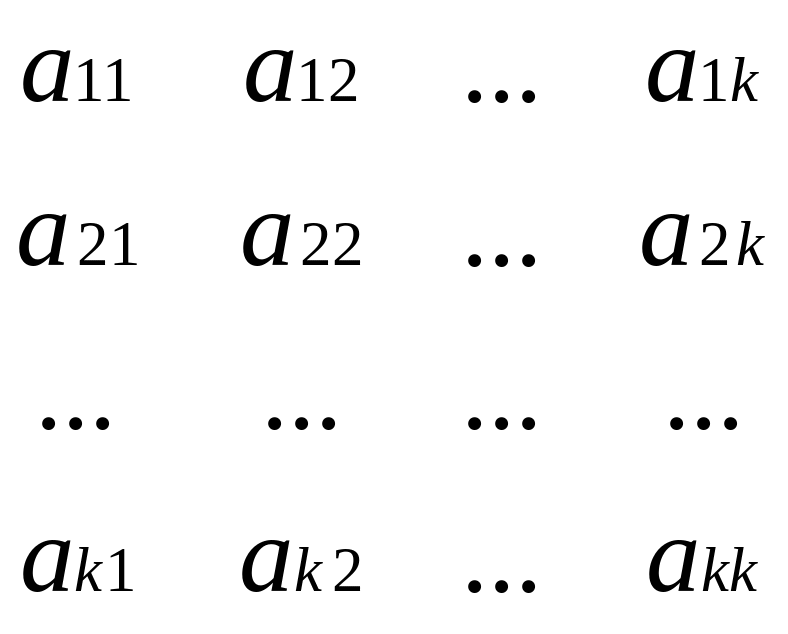
U k H ρ
Рисунок 4.2 – Производящая матрица
Для построения производящей матрицы удобно U k брать в виде квадратной единичной:
U
k
=
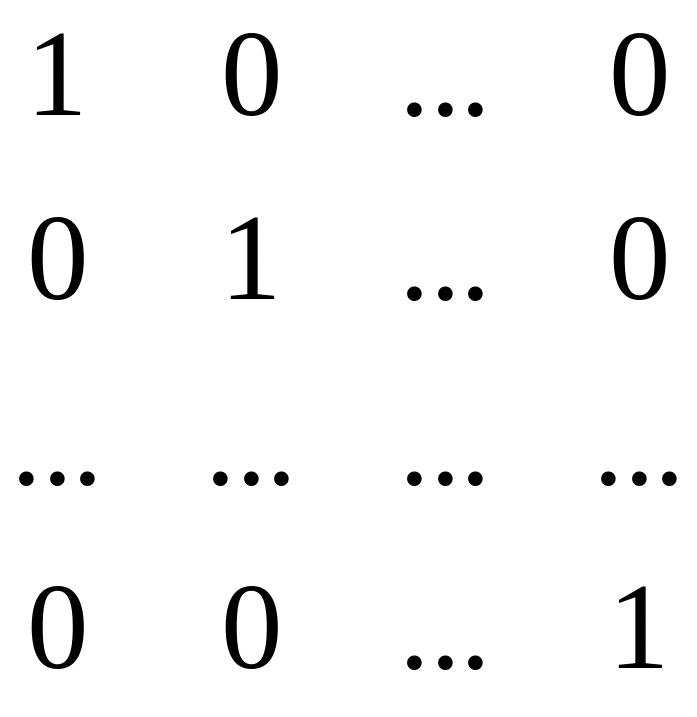
Рисунок 4.3 – Информационная матрица
Тогда матрица Pn,k в канонической форме:
P n,k =
Рисунок 4.4 – Проверочная матрица
При этом проверочная матрица H ρ строится так:
количество единиц в строке должно быть ≥ (d min - 1);
двух любых строк должна содержать ≥ (d min - 2) единиц.
Проверочные символы образуются линейными операциями над информационными символами.
Для каждой кодовой комбинации нужно составить ρ независимых сумм по mod 2.
Для этого удобно использовать проверочную матрицу Н. Сначала строят подматрицу Н’ – транспонированную матрицу H ρ:
Н’
=
Рисунок 4.5 – Транспонированная матрица Н’
Затем справа приписывается единичная матрица:
Н =
Рисунок 4.6 – Матрица Н
Проверочные символы по матрице Н находятся так:
позиции, занимаемые единицами в первой строке подматрицы Н’, определяют информационные разряды, участвующие в формировании первого проверочного разряда кодовой комбинации;
позиции, занимаемые единицами во второй строке подматрицы Н’, определяют информационные разряды, участвующие в формировании первого проверочного разряда кодовой комбинации и т.д….
Пример: построить линейный систематический код для информационной комбинации 0011 (k = 4) по производящей матрице Р7,4:
P
7,4
=
Рисунок 4.7 – Образующая матрица Р7,4
Т.е. проверочная матрица:
Н 3 =
Рисунок 4.8 – Проверочная матрица Н3
Тогда транспонированная матрица:
Н’
=
Рисунок 4.9 – Транспонированная матрица Н’
Приписываем справа единичную матрицу:
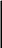a1
a2
a3
a4
b1
b2
b3
Н
=
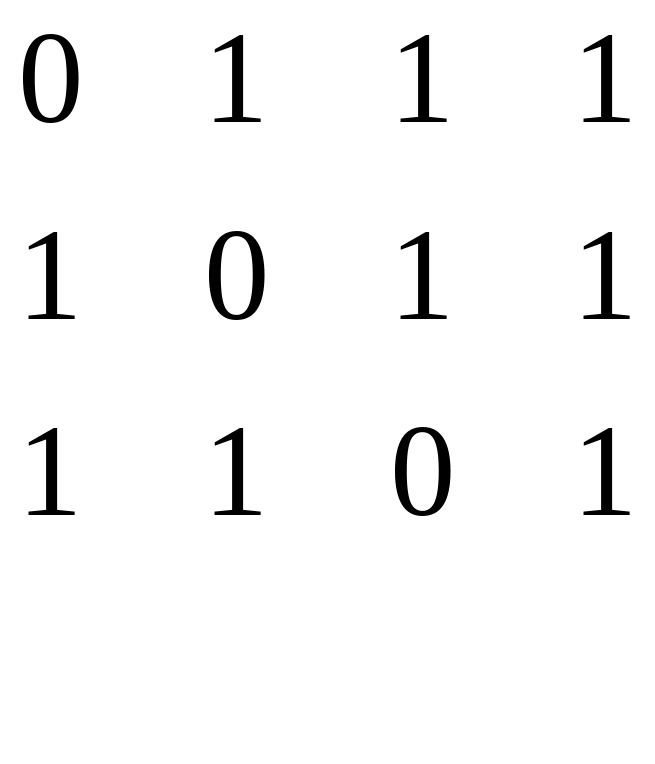
Рисунок 4.10 – Матрица Н
Кодовая комбинация должна содержать ρ проверочных символов:
ρ = n – k = 7 – 4 = 3.
Нужно найти три проверочных символа: b1, b2, b3.
Из подматрицы Н’ определяем:
b1 = a2 a3 a4
b2 = a1 a3 a4
b3 = a1 a2 a4
Тогда для нашего сообщения 0011 проверочные символы будут:
b1 = 0 1 1 = 0
b2 = 0 1 1 = 0
b3 = 0 0 1 = 1
a1 a2 a3 a4 b1 b2 b3
Полная кодовая комбинация будет: 0 0 1 1 0 0 1 .