
- •Часть 1
- •Содержание
- •Общие сведения по проведению лабораторных работ
- •Лабораторная работа №1 о пределение теплопроводности твердых материалов методом пластины
- •Цель работы
- •1.2Экспериментальная установка
- •1.3Порядок проведения опытов.
- •1.4Обработка результатов.
- •1.5 Контрольные вопросы к лабораторной работе
- •Лабораторная работа№2 исследование теплоотдачи при естественной конвекции около горизонтального цилиндра методом имитационного моделирования процесса теплообмена
- •2.1 Цель работы
- •2.2Экспериментальная установка
- •2.3Порядок проведения опытов.
- •2.4Обработка результатов.
- •2.6 Контрольные вопросы к лабораторной работе
- •Лабораторная работа№ 3 исследование теплоотдачи при естественной конвекции около вертикального цилиндра в атмосфере различных газов методом имитационного моделирования процесса теплообмена
- •3.1 Цель работы
- •3.2Экспериментальная установка
- •3.3Порядок проведения опытов.
- •3.4Обработка результатов.
- •3.6 Контрольные вопросы к лабораторной работе
- •Лабораторная работа № 4 исследование теплоотдачи при вынужденном движении воздуха в трубе методом имитационного моделирования процесса теплообмена
- •4.1 Цель работы
- •4.2Экспериментальная установка
- •4.3 Порядок проведения опытов
- •4.4Обработка результатов.
- •4.5 Контрольные вопросы к лабораторной работе
- •Лабораторная работа №5 определение коэффициента излучения электропроводящих материалов калориметрическим методом
- •5.1 Цель работы
- •5.2Экспериментальная установка
- •5.3Порядок проведения опытов.
- •5.4Обработка результатов.
- •5.5 Контрольные вопросы к лабораторной работе
- •Библиографический список
- •Приложение а
3.4Обработка результатов.
1. Для определения локального коэффициента теплоотдачи a согласно закона Ньютона необходимо рассчитать конвективный тепловой поток Qк, поскольку все остальные величины Тwі, Т¦, F измерены. Qк определяется из баланса энергии: Qк=Qэ-Qu, так как электрическая мощность Qэ, затраченная на нагревание исследуемого цилиндра, отдается в окружающую среду как свободной конвекцией Qк, так и излучением Qu.
Электрическая мощность, подводимая к цилиндру, рассчитывается по формуле
 ,
Вт(1)
,
Вт(1)
где R=0,0195 Ом – омическое сопротивление цилиндра.
Лучистый тепловой поток рассчитывается по формуле
,Вт(2)
где Тwі и Т¦ – температура стенки в і-ой точке и окружающего воздуха, К;
С0 = 5,7 Вт/(м2 К4) – коэффициент излучения абсолютно черного тела;
e =0,2 – степень черноты поверхности стального цилиндра;
F=pDнарL – площадь боковой поверхности вертикального цилиндра, м2.
Коэффициент теплоотдачи
 ,
Вт/(м2
К) (3)
,
Вт/(м2
К) (3)
где Dнар=0,02 м – наружный диаметр цилиндра,
L=0,5 м – длина цилиндра,
DТі= Тwі- Т¦– температурный напор в местах заделки термопар, К;
2. Находится значение определяющей температуры по формуле:
 (4)
(4)
где Тwср – среднее значение температуры стенки, К.
3. По найденному значению определяющей температуры выписываются из приложения теплофизические параметры (l,n,Rr) и подсчитывается объемный коэффициент расширения b = 1/ Тm.
4. Вычисляются критерии подобия
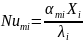 (5)
(5)
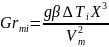 (6)
(6)
 (7)
(7)
5. Результаты обработки опытных данных сводятся в таблицу 3.2.
6. Полученные значения критериев подобия наносятся на график, построенный в логарифмических координатахlgNum, lg(GrmPrm) (рис. 3.2) и аппроксимируются прямой линией, тангенс угла наклона которой определяется значение показателяnв критериальной зависимости: Numx = C (GrmxPrm)n.
Значение постояннойС определяется из выражения по любой точке аппроксимирующей прямой.
7. Аналогичные действия по пп.4 и 6 выполняются для определяющей температуры Т¦.
8. Сопоставляются экспериментально полученные зависимости Nux= C(GrxPr)п с теоретическими для ламинарного и турбулентного режимов течения.
Ламинарный режим течения реализуется приGrfxPrf<109 и теоретическая зависимость имеет вид:
Nu¦х = 0,56 (GrfxPrf)0,25(8)
Турбулентный режим течения в пограничном слое реализуется при GrfxPrf³ 6×1010, в данном случае теоретическая зависимость имеет вид:
Nu¦x= 0,13 ( Gr¦xPr¦)1/3(9)
В данной работе может реализоваться сразу оба режима течения в зависимости от исследуемой газовой среды, ламинарный и турбулентный, и экспериментальные результаты аппроксимируются двумя прямыми с различным наклоном, и соответственно получаются два значения показателя степени n1 и n2 при (Gr¦xPr¦) и постоянной С1 и С2.
9. Строится график зависимости коэффициента теплоотдачи вдоль вертикальной стенкиaі = ¦ (xі).
3.5Оценка погрешностей результатов исследований
Специфика методики по оценкепогрешностейзаключается в том, что в даннойлабораторнойработеиспользуетсяимитационноемоделированиережимовнагрева и теплообмена по жесткойпрограмме, заложенной в память ЭВМ, согласнокоторой переход с одного режима на другой осуществляется ступенчато, а значения падения напряжения и температуры поверхности на экспериментальном участке строго фиксированы. Измерительная информация снимается с помощью установленных на пульте управления измерительных приборов и отображается на экране телевизионного монитора. Поэтому при обработке результатов экспериментов на имитационной установке для каждого режима нагрева и теплообмена необходимо учитывать класс применяемого измерительного прибора и его допустимые погрешности измерений в соответствии с метрологическими требованиями ГОСТ 8.009-84 и ГОСТ 8.508-86.
Так как при выполнении работы на каждом заданном стационарном режиме проводится однократное измерение электрических и температурных параметров, то рекомендуется следующий порядок расчета при оценке погрешностей.
Определяется класс точности измерительных приборов и оценивается погрешность измерения величины в выбранном диапазоне измерений. Предел допустимой основной погрешности средств измерений оценивается по формуле:
(10)
где Хн – нормируемое значение измеряемой или определяемой допустимой величины;
g - предел допустимой погрешности прибора (класс точности прибора).
С учетом, что конвективный тепловой поток определяется из уравнения баланса
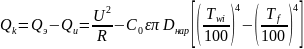 (11)
(11)
Среднеквадратическая относительная погрешность конвективного теплового потока Qк рассчитывается по формуле
 (12)
(12)
Так как коэффициент теплоотдачи aі определяется по закону Ньютона
 (13)
(13)
то среднеквадратическая относительная погрешность в определении местного коэффициента теплоотдачи a рассчитывается по формуле:
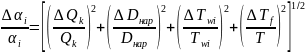 (14)
(14)
В приведенных формулах D обозначены абсолютные погрешности измерения величин напряжения U, температур Тwі и Т¦, диаметра Dнар и длины цилиндра L.
Абсолютные погрешности указанных величин принимаются равными 0,5%.

Рисунок 3.2 – Зависимость lgNu= lgC(GrPr)n в логарифмических координатах
