3.2. Расчет вала на жесткость

Для исключения недопустимо больших деформаций оценивается жесткость вала по значениям прогибов f в местах установки зубчатых колес (дисков), а также углов поворота сечений  на опорах.

Условия жесткости представляются в виде

, ,

(3.14)

где [f] и [] – допускаемые значения линейных прогибов и углов поворота соответственно.

Допускаемый прогиб вала принимается в пределах [f]=(1,0…5,0)10^-4l₀, где l₀ – расстояние между опорами.

Допускаемый угол поворота определяется типом подшипника и принимается порядка [] = (0,0025…0,0050) рад.

Для определения прогибов f и углов поворота  в сечениях предварительно любым из известных методов (начальных параметров, способом Мора, по правилу Верещагина) рассчитываются прогибы и углы поворота в вертикальной (f_y, _x) и горизонтальной (f_x, _y) плоскостях. Затем определяются их полные значения

; .

(3.15)

Если оба условия жесткости (3.14) выполняются, то значение диаметра вала d, выбранное из условия прочности, используется для дальнейших расчетов.

При невыполнении условий жесткости (3.14) находятся новые значения диаметра

, ,

(3.16)

наибольшее из которых принимается за расчетное (d_расч). Это значение округляется до ближайшего большего стандартного значения, как рекомендуется в разделе 3.1.

3.3. Проверочный расчет вала на усталостную прочность

Основные расчетные зависимости. Вследствие вращения и многократной повторяемости нагружения и разгрузки в течение срока службы вал испытывает переменные напряжения, которые могут вызвать усталостные разрушения. Поэтому после выбора диаметра из условий статической прочности и жесткости и конструирования вала необходимо проверить его на усталостную прочность.

Условие усталостной прочности имеет вид

.

(3.17)

Допускаемое значение запаса прочности для деталей общего машиностроения [2] принимается в пределах [n] = 1,5…2,5, а запас прочности, соответствующий плоскому напряженному состоянию в опасной точке сечения (рис. 3.1, в), определяется по формуле

,

(3.18)

в которой – запасы прочности по нормальным и касательным напряжениям соответственно.

Эти запасы рассчитываются по формулам

, ,

(3.19)

где и – пределы выносливости материала при симметричных циклах изменения нормальных и касательных напряжений; , и , – соответственно амплитудные и средние значения напряжений;

(3.20)

В последние формулы входят следующие коэффициенты, учитывающие влияние на прочность конструктивных и технологических факторов [1, 2]:

• , – эффективные коэффициенты концентрации напряжений;

• , – коэффициенты влияния абсолютных размеров (масштабный фактор);

• , – коэффициенты влияния состояния (качества) поверхности деталей;

• – коэффициент влияния поверхностного упрочнения;

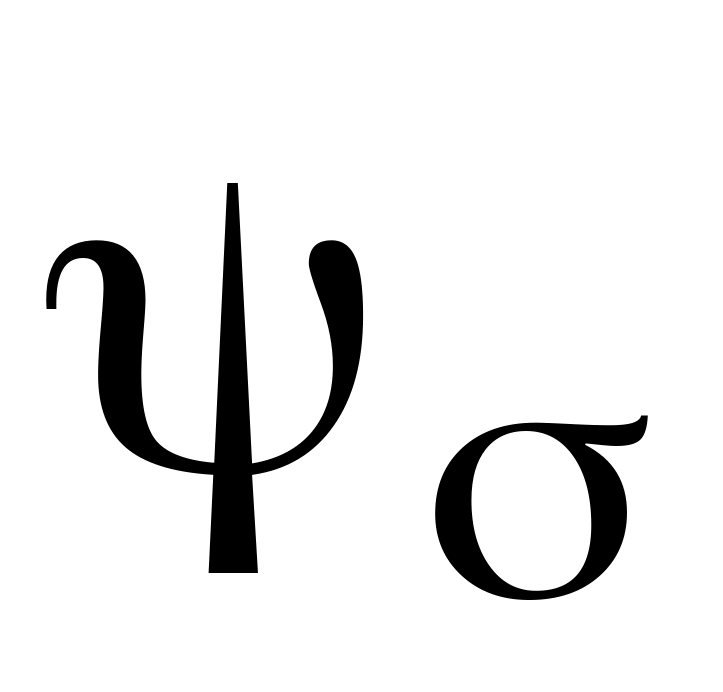• , – коэффициенты чувствительности материала к асимметрии цикла.

Из формул (3.19) ясно, что расчет запасов прочности и , а затем n по зависимости (3.18) можно выполнить лишь зная конструкцию вала, в частности в районе опасного сечения, и технологию его изготовления.

В формулы (3.20) входят отношения эффективных коэффициентов концентрации напряжений к масштабным факторам , . Эти коэффициенты определяются в результате усталостных испытаний и приводятся в машиностроительных справочниках для конкретных размеров валов. Если для расчетных размеров валов нет данных, то рекомендуется их найти интерполяцией (например, линейной). Для более точного вычисления этих отношений в [2] предложены формулы (например, для сталей, алюминиевых и магниевых сплавов)

или при кручении ,

где L – линейная протяженность очага концентрации (для круглого вала, например, [2], d – номинальный диаметр вала), 88,3 – коэффициент, мм² (поэтому и L следует поставлять в миллиметрах); , – показатели степени, постоянные для данного материала. Для углеродистых сталей, например, = 0,1…0,14, для легированных сталей = 0,04…0,08 [2]. Для значений здесь же рекомендовано простое соотношение .

Относительный градиент и теоретический коэффициент концентрации напряжений – параметры, характеризующие особенности местных напряжений. Введение в расчет градиента не требует специального решения каких-либо новых задач. В каждом конкретном случае их определяют одновременно [2].

Для некоторых концентраторов напряжений формулы для относительного градиента приведены в [7]. Значения теоретических коэффициентов концентрации напряжений , можно найти в [5].

Конструирование участка вала и выбор метода обработки. В зависимости от положения опасного сечения, установленного при расчете вала на статическую прочность, выбирается фрагмент участка вала (см. приложения): либо это сопряжение вала с подшипником (опора), либо – соединение с зубчатым колесом или шкивом.

Вопросы, связанные с конструированием, методами обработки поверхностей шеек валов, рассматриваются в последующих курсах (детали машин и основы конструирования, материаловедение, технология машиностроения и др.). Конструирование расчетного участка ведется с учетом следующих рекомендаций:

1) для обеспечения равнопрочности, упрощения технологии изготовления и фиксации насаживаемых на вал деталей (колес, подшипников и пр.) в осевом направлении, валы делают ступенчато-переменного сечения. Высота упорного буртика t определяется радиусом галтельного перехода r и величиной фаски f : t > r+f [3]. Последние в зависимости от номинального диаметра вала можно принять по табл. 3.2 [5].

Таблица 3.2

Значения высоты буртика t и радиус скругления r в зависимости

от диаметра d шейки вала (в мм)

d	17…24	25…30	32…40	42…50	52…60	62…70
t	2	2,2	2,5	2,8	3	3,3
r	1,6	2	2,5	3	3	3,5
f	1	1	1,2	1,6	2	2

Шейки валов, где насаживаются зубчатые колеса и подшипники (в последнем случае обязательно) шлифуются. Размеры канавки для выхода шлифовального круга и радиусы стандартизованы [1] табл. 3.3.

Таблица 3.3

Канавки для выхода шлифовального круга (по ГОСТ 8820-69)

b, мм	d1, мм	r, мм	d, мм
2	d – 0,5	0,5	До 10
3		1	Св. 10 до 50
5	d – 1	1,6	Св. 50 до 100
8		2,0	Св. 100

Коэффициенты концентрации напряжений для ступенчатого перехода с галтелью приведены в табл. П4 [1].

2) Соединение зубчатых колес, шкивов ременных и звездочек цепных передач с валами осуществляются призматическими шпонками, шлицами (прямобочными) и, редко колес, подшипников обязательно – за счет посадки с натягом. В табл. П5 – П7 приведены соответствующие для каждого из этих вариантов соединения значения коэффициентов концентрации [4]. Причем для последнего случая в табл. П7 приведены отношения коэффициентов концентрации к масштабному фактору, так что последние отдельно определять нет необходимости.

3) Часто закрепление распорных втулок на валах осуществляется коническими или цилиндрическими штифтами. Диаметр d₀ поперечного отверстия под штифт принимают равным (0,01 – 0,25) d и округляют по ГОСТ 3128-70 (ИСО 2338-86) (d₀ в мм: 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20) [3]. Коэффициенты концентрации напряжений для этого случая приведены в таблице П8.

При наличии в опасном сечении наружной метрической резьбы предусматривают проточки по ГОСТ (табл. 3.4 [3]), а коэффициенты концентрации напряжений – в табл. П9 [1].

Таблица 3.4

Размеры проточек для выхода резьбообразующего инструмента (ГОСТ 10549-80), мм

шаг резьбы	b	r	d3
1	3,6	2	d - 1,5
1,25	4,4	2,5	d - 1,8
1,5	4,6	2,5	d - 2,2
1,75	5,4	3	d - 2,5
2	5,6	3	d - 3
2,5	7,3	4	d - 3,5
3	7,6	4	d - 4,5

Разработанный эскиз участка вала вычерчивается в масштабе в соответствии с существующими правилами черчения.

Значения масштабного фактора в зависимости от материала вала и величины номинального диаметра приведены в табл. П10 [1].

При установлении вида обработки и чистоты поверхности необходимо иметь в виду следующее:

• все посадочные поверхности вала шлифуют;

• шпоночные пазы и шлицы изготавливают фрезерованием;

• отверстия под штифты получают сверлением с последующей разверткой;

• резьбу, проточки под стопорные кольца, радиусные (галтельные) переходы и свободные поверхности вала обрабатывают тонким точением;

• подшипники монтируют на валу по посадкам с натягом.

Числовые значения коэффициентов, учитывающих состояние поверхности и упрочнения приведены в табл. П11 и П12 [1].

Выбор расчетных сечений. В зависимости от конструкции опасного участка вала устанавливается тип и число концентраторов напряжений и выбираются расчетные сечения.

Расчет характеристик циклов переменных напряжений. Для каждого из выбранных расчетных сечений определяются характеристики циклов изменения напряжения.

При этом учитывается, что вследствие вращения вала напряжения изгиба меняются по симметричному циклу, а напряжения растяжения (сжатия) постоянны. Таким образом, нормальные напряжения  в расчетных сечениях меняются по асимметричному циклу (рис. 3.4, а) с параметрами:

• амплитуда напряжений

  ,

  (3.21)

• среднее напряжение

.

(3.22)

Рис. 3.4

В течение срока службы вал испытывает многократное повторное нагружение и разгрузку, тогда касательные напряжения кручения меняются по пульсирующему циклу (рис. 3.4, б). Параметры такого цикла:

.

(3.23)

Примечание. В практических расчетах амплитуды и средние значения нормальных и касательных напряжений вычисляют для опасного сечения по номинальному диаметру вала, т.е. для всех расчетных сечений принимают одинаковыми. Очевидно, погрешность такого упрощения идет в запас прочности.

Выбор расчетных коэффициентов. Коэффициенты , ; , ; , ; ; , , входящие в расчетные зависимости (3.18) – (3.20) для , , выбираются для каждого расчетного сечения по вышеприведенным таблицам и графикам, имеющимся в справочной литературе [2,3,5].

Расчет коэффициентов запаса и оценка усталостной прочности. Для каждого из расчетных сечений по формулам (3.19), (3.18) рассчитываются коэффициенты запаса прочности , , , затем проверяется условие (3.17) усталостной прочности и делается необходимый вывод.

4	ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕ РАБОТЫ

1. Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением?

2. Как находятся опасные сечения стержня круглого сечения при изгибе с кручением?

3. Какие точки круглого поперечного сечения являются опасными при изгибе с кручением? Какое напряженное состояние имеет место в этих точках?

4. Как находится величина эквивалентного (приведенного) запаса прочности по различным теориям прочности при изгибе с кручением вала? Сделайте вывод соответствующих формул.

5. Как производится расчет на статическую прочность при изгибе с кручением?

6. Как оценивается жесткость вала?

7. Как находится полный прогиб вала в месте посадки дисков (колес)?

8. Как находится полный угол поворота в опоре вала?

9. Какими способами могут быть вычислены обобщенные перемещения?

10. Как устанавливаются допускаемые значения обобщенного перемещения?

11. Что такое действительное (или грузовое) и единичное (или фиктивное) состояние?

12. Как производится перемножение эпюр по правилу Верещагина?

13. Как по правилу Верещагина производится перемножение эпюр, ограниченных ломаными линиями?

14. Какими величинами характеризуется цикл изменения напряжений? Что такое симметричный и асимметричный циклы?

15. Что такое кривая усталости (кривая Велера) и как ее строят?

16. Что называют пределом усталости (выносливости)?

17. Как влияют размеры детали на величину предела усталости? Что такое масштабный фактор и от чего он зависит?

18. Что такое эффективный коэффициент концентрации напряжений и коэффициент чувствительности материала к концентрации напряжений? Как они связаны между собой и от каких факторов зависят?

19. Как влияет на величину предела усталости характер обработки поверхности детали? Что называется коэффициентом качества поверхности?

20. Какой вид имеет условие усталостной прочности?

21. Как определяется коэффициент запаса прочности при симметричном и асимметричном циклах в случаях растяжения, сжатия, кручения и изгиба?

22. Как определяется коэффициент запаса усталостной прочности вала, работающего на совместное действие изгиба с кручением?

5	ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

ЗАДАНИЕ. На вал установлены два зубчатых колеса диаметрами D₁ и D₂, нагруженные силами от сопряженных колес (рис. 5.1, а).

Необходимо:

– подобрать диаметр вала d из условия статической прочности. В опасном сечении вала построить эпюры нормальных и касательных напряжений и показать напряженное состояние тела в опасной точке;

– произвести расчет вала на жесткость по линейным перемещениям в местах установки колес и по угловым перемещениям в опорах. Уточнить диаметр вала;

– выполнить проверочный расчет вала на усталостную прочность в двух опасных сечениях (рис. 5.1, б, в).

Рис. 5.1

Исходные расчетные данные

T, Нм	l1, м	l2, м	l3, м	D1, м	D2, м	,град	Марка стали
500	0,1	0,2	0,12	0,2	0,40	30	40ХН

5.1. проектировочный расчет вала на статическую прочность

При расчете на статическую прочность представим вал AB в виде балки на двух опорах. Одну из опор примем как неподвижный шарнир (сечение С), другую, как наиболее близко расположенную к коническому колесу, – как подвижный шарнир (сечение В, рис. 5.2, а).

По формулам табл. 3.1 определим действующие на колеса силы:

Окружные силы:

Нм; Нм;

радиальные силы

Н;

Н;

осевая сила на конической шестерне

Н.

Заменим действие установленных на вал колес соответствующими силами и моментами. Векторы радиальных сил R₁ и R₂ перенесем в центр тяжести сечения вала по линии их действия. Векторы окружных сил P₁ и P₂ – параллельно самим себе. При этом появятся два крутящих сосредоточенных момента Нм в сечениях A и D соответственно.

Перенесем вектор силы N₁ на ось вала. При этом в сечении D возникнет сосредоточенный изгибающий момент равный

Нм.

Силовые факторы, лежащие в вертикальной плоскости, вызовут в подшипниках реакции R_Cy и R_By, а в горизонтальной – R_Cx и R_Bx. Величины этих реакций определим, как для балки, лежащей на двух опорах.

Видно (рис. 5.2, а), что вал работает на совместное действие растяжения (сжатия), кручения и изгиба в вертикальной (yAz) и горизонтальной (xAz) плоскостях. Рассмотрим каждую деформацию отдельно, используя принцип независимости действия сил.

Для нахождения опасной точки вала установим, как меняются по длине вала внутренние силовые факторы, то есть построим их эпюры.