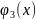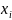ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

КУРСОВАЯ РАБОТА

ЗАЩИЩЕНА С ОЦЕНКОЙ

РУКОВОДИТЕЛЬ

С. Л. Козенко

должность, уч. степень, звание

подпись, дата

инициалы, фамилия

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ

АППРОКСИМАЦИЯ ФУНКЦИИ МЕТОДОМ НАИМЕНЬШИХ

КВАДРАТОВ

по дисциплине: ИНФОРМАТИКА

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. 2633 К. В. Попов

подпись, дата инициалы, фамилия

Санкт-Петербург

2017

СОДЕРЖАНИЕ

1. Цель работы ………………………………………………………………………. 3

2. Постановка задачи ………………………………………………………………... 3

3. Представление исходных данных (табличное) …………………………………. 3

4. Описание метода выбора аппроксимирующей функции……………………….. 4

5. Описание метода вычисления коэффициентов нормальных уравнений………. 4

6. Описание метода Гаусса ………………………………………………………….. 6

7. Ручной счёт ……………………………………………………………………….. 7

8. Схемы алгоритмов и их описание ………………………………………………… 10

   1. Общая схема алгоритма ……………………………………………………..... 10

   2. Схемы алгоритмов вычисления коэффициентов 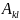и

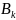
системы нормальных уравнений …………………………………………….. 11

8.2.1 Схема алгоритма функции 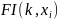………………………………………… 11

8.3 Схема алгоритма решения системы линейных уравнений методом Гаусса.12

8.3.1 Обобщённая схема алгоритма метода Гаусса ……………………………… 12

8.3.2 Схема алгоритма прямого хода метода Гаусса …………………………….. 12

8.3.3 Схема алгоритма определения ведущего элемента………………………… 13

8.3.4 Схема алгоритма перестановки уравнений ………………………………… 14

8.3.5 Схема алгоритма расчёта коэффициентов уравнений ……………………... 15

8.3.6 Схема алгоритма обратного хода метода Гаусса …………………………... 15

8.4 Схема алгоритма вычисления значений критерия аппроксимации,

максимального отклонения и его координаты ………………………………. 16

9. Программа и результаты расчётов параметров на компьютере………………… 17

10. Заключение …………………………………………………………………………. 20

1. Цель работы

Данная курсовая работа завершает дисциплину «Вычислительная математика и программирование» и требует от студента в процессе её выполнения решения следующих задач:

1) Практического освоения типовых вычислительных методов прикладной математики;

2) Совершенствование навыков разработки алгоритмов и построения программ на языке высокого уровня;

Практическое выполнение курсовой работы предполагает решение типовых инженерных задач обработки данных с использованием методов матричной алгебры и методов решения систем линейных алгебраических уравнений. Навыки и знания, приобретаемые в процессе выполнения курсовой работы, позволят использовать вычислительные методы прикладной математики и техники программирования в процессе изучения всех последующих дисциплин.

2. Постановка задачи

При изучении зависимостей между некоторыми величинами важной задачей является приближенное представление (аппроксимация) этих зависимостей с помощью известных функций или их комбинаций, подобранных надлежащим образом.

Исходная функциональная зависимость представлена таблично. Требуется найти параметры аппроксимирующей функции используя метод наименьших квадратов. Поиск параметров осуществлять при помощи метода Гаусса. Оценить погрешность аппроксимации посредством критерия качества I и максимальное по модулю отклонение аппроксимирующей функции от исходной.

3. Представление исходных данных

Номер варианта	n	Заданные точки						Базисные функции			Метод решения
21	5		0,32	0,52	0,72	0,92	1,12	1				Метод Гауссаcа
			3,4	2,15	1,15	0,35	3,1

4. Описание критерия аппроксимации и способа его минимизации:

Аппроксимация - метод, состоящий в замене одних объектов другими ,в том или ином смысле близкими к исходным ,но более простыми.

– нахождение ошибки

На основе изучения ошибок формируются различные аппроксимации .Один из распространённых подходов это метод наименьших квадратов (МНК), в соответствии с которым достигается наименьшая сумма квадратов ошибок δ.

Требование имеет вид:

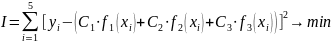
5. Описание метода вычисления коэффициентов нормальных уравнений:

Метод МНК – один из методов регрессионного анализа для оценки неизвестных по результатам измерений, содержащих следующие ошибки.

Система нормальных уравнений примет вид:

Обозначения:

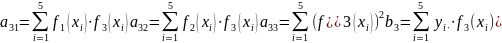
Матрица системы:

Вектор-столбец свободных членов:

Вектор-столбец неизвестных:

6. Описание метода Гаусса

Метод Гаусса – это классический метод решения СЛАУ. Этот метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого(или треугольного)вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Осуществляется «прямой ход», когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме ,либо устанавливают ,что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой ,перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, умножив её на величину ,равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные действия были совершенны, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой элемент ,то переходят к следующему столбцу и проделывают аналогичную операцию.

Пример:

,

,

, ,
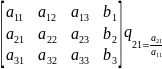
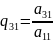
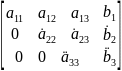